5.4 First Law of Thermodynamics

The First Law of Thermodynamics applies the principle of energy conservation to the boundaries of a system of interest. The First Law says that the change in internal energy is equal to the heat added to the system minus the work done by the system to the surroundings. This is written \[\begin{equation} \Delta U = Q - W \tag{5.1} \end{equation}\] where

$\Delta U$ is the change in internal energy,
$Q$ is the heat added to the system,
and $W$ is the work done by the system to the surroundings.

Equation (5.1) can also be written in differential form as \[\begin{equation} dU = \delta Q - \delta W \tag{5.2} \end{equation}\]

This formulation is important for describing infinitesimal changes and reversible processes. Thermodynamics texts often use $d$ and $\delta$ symbols to make the distinction between exact and inexact differentials, respectively. To clarify this consider the following example. If we were to call the internal energy of an ideal gas system $U_A$ at state A, then as we will discuss in more detail later, the state variables of the system are $P$ for pressure, $V$ for volume, and $T$ for temperature which together specify $U_A$. Now if the system changes to a new state B, where $U_B = f (P_B,V_B, T_B)$, we know that this change in state is described by equation (5.2). However, work and heat cannot be uniquely expressed in terms of the system variables $P$, $V$ and $T$. Thus, although we know the magnitude of the difference for the change of state, $dU$, we cannot resolve it into components of heat and work. The total change in $W$ and $Q$ depends upon the particular “path” through which the system goes from $U_A$ to $U_B$ (see Figure 5.4 for a simplified representation which is described in detail later), i.e., the path of integration of $\delta W$ and $\delta Q$ between $U_A$ and $U_B$. The inexact differential, $\delta$, is used to remind the reader of this fact.

One will find other sign conventions for the First Law. Here, we defined $dU$ to be positive when the energy flows into the system. Therefore the heat $Q$ flows into the system adds to its internal energy while the work $W$ done by the system subtracts from the internal energy. It is important to realize that once a convention has been agreed upon one must be consistent to account properly for the changes in the internal energy of the system.

The units of equation (5.1) are energy units. A variety of different units are used in the engineering as well as the biological literature. The calorie is a common unit for biological measurements. It is defined as the energy necessary to raise one gram of water from $14.5^{\circ}C$ to $15.5^{\circ}C$ at atmospheric pressure. We will use the International System of Units (SI), consistent with most scientific research. Therefore, the joule will be used as the basic energy unit. Appendix I is included to help the reader with units. One may also wish to review the module devoted to units and dimensions. Furthermore, the student should also be aware that the First Law is often used with other dimensions such as (1) energy per unit area, (2) energy per unit time (power or flux), and (3) power per unit area (flux density).

5.4.1 Internal Energy

The internal energy $U$ is often intended to mean the thermal energy of the system represented by its temperature. In general, the chemical energy, or the energy holding atoms together, of the system is included as part of the internal energy function. Many studies have measured the energy flows of ecological systems to learn about trophic levels, food webs, and ecological transfer efficiencies. Commonly, the mass of each standing crop and the flow are measured and then converted into total chemical energy by a laboratory procedure such as bomb calorimetry. The thermal internal energy is the vibrational energy of the molecules and is indicated by the temperature of the system. In most instances there will be no structural changes of the material within the range of temperatures normally found in the environment. The most common exception of thermobiological importance is the increase of internal energy of H₂O during melting (ice to liquid), sublimation (ice to vapor) and evaporation (liquid to vapor) (See Figure 5.1.)

5.4.2 Heat and Heat Transfer Processes

The second term, $Q$, in the equation for the First Law of Thermodynamics is called heat. Heat is energy in transit. Heat transfer is a spontaneous process in which heat flows from warmer objects to colder objects. The study of heat transfer involves measuring the rate and magnitude of heat flow.

There are four kinds of heat transfer mechanisms relevant to this discussion: (1) conduction, (2) convection, (3) radiation, and (4) evaporation. Conduction describes the physical process of thermal energy transport in solids. Examples are heat flow in soils, between animals and the ground, and between animals that are in bodily contact. Convection is the transfer of heat between solids and fluids (i.e., gasses and liquids) or when fluids of different temperatures are in contact. The wind blowing over or around a leaf is one example. Conduction takes place with nearby particles but the additional factor of the circulation of the fluid distinguishes convection from conduction. If there is no motion in the fluid except that caused by the heat transfer the process is called free convection. If the fluid is moving relative to the other fluid or solid, the process is called forced convection. Convection is a complex process involving heat transfer and fluid dynamics.

The process by which energy can be transmitted without the presence of an intervening medium is called radiation. All objects, living and nonliving, radiate energy. The amount and kind (wavelength in the electromagnetic spectrum) of energy depends on the temperature and physical characteristics of the radiating body. Figure 5.2 shows the electromagnetic spectrum, which is characterized by either of two scales, frequency $f$ or wavelength $\lambda$, (the scales are inversely proportional). Radiation is a field phenomenon having both particulate (photons) and wave characteristics. Acoustic waves, however, require an intervening medium. The physics of radiation is described in greater detail in other modules.

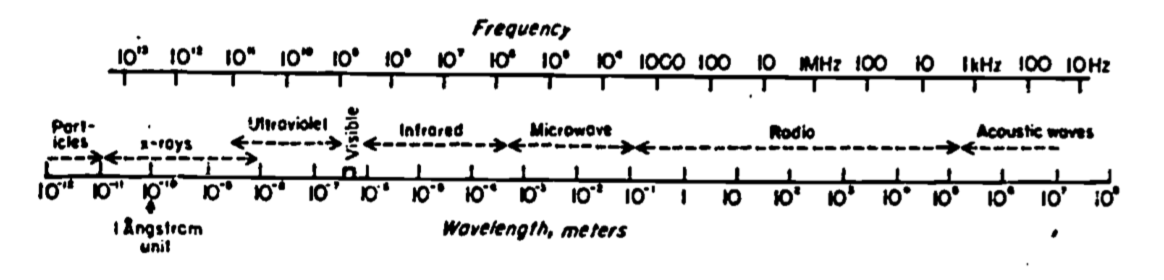
$Electromagnetic spectrum as a function of both frequency (f) (Hertz or cycles sec) and wavelength ($\lambda$) (meters). From Byers, H.R. 1974. General Meteorology. P. 8.$

Figure 5.2: Electromagnetic spectrum as a function of both frequency (f) (Hertz or cycles sec) and wavelength ($\lambda$) (meters). From Byers, H.R. 1974. General Meteorology. P. 8.

The last heat transfer process important in the heat term of the First Law is evaporation. Evaporation is the process that transports water by changing it from a liquid to a gas. For animals, water vapor may be lost during respiration, through special sweat glands, or through any part of the skin. The physiology of the species must be known to estimate this heat and mass flow. Higher green plants lose water vapor to the atmosphere through stomata in a process called transpiration. The physics of this heat transfer process will also be presented in a later module.

Before considering work, the last term of eq. (5.2), we will define the heat capacity. It is \[\begin{equation} C_x = (\frac{\delta Q}{dT})_x \end{equation}\] where $x$ is some state variable such as pressure, volume or temperature for a gas system. By specifying $x$, one indicates the path of the process as well as its reversibility. For $P$, $V$, $T$ systems it is customary to define

\[\begin{equation} C_V = (\frac{\delta Q}{dt})_V \tag{5.3} \end{equation}\]

and \[\begin{equation} C_P = (\frac{\delta Q}{dT})_P \tag{5.4} \end{equation}\] In eq. (5.3) $V$ means that the process of adding heat to the system is carried out at constant volume. $C_V$ represents the proportionality constant for the change in temperature per unit amount of heat added. Similarly in eq. (5.4) $P$ stands for a constant pressure process.

5.4.3 Work

To complete the introduction of the First Law of Thermodynamics we need to examine the concept of work. When considering work we usually think of mechanical work, which is a force times a distance operating in some system. In this module work is done by the system on the surroundings, thus decreasing the system’s energy. Furthermore we consider only external work and are not concerned with processes that go on inside the system.

If our system is an organism then we would not be concerned with the work associated with internal chemical reactions. On the other hand if the system of interest is the heart then one would wish to know the work done by the heart on the rest of the body.

To illustrate work and the other terms in the First Law we use the classical thermodynamic example of the gas in a piston. This example is also of historical importance because one motivation for the development of thermodynamic theory was to describe and predict the behavior of steam engines, which used heated water vapor as a source of energy to derive mechanical work. Figure 5.3 depicts the system of interest where the thick line represents the boundary enclosing the system, in this case a gas. Here the work done by the system is \[\begin{equation} \delta W = PdV \tag{5.5} \end{equation}\]

where $P$ is the external pressure. For reversible processes the system pressure can be used. Figure 5.4 shows a plot of $P$ versus $V$. To calculate the work done we need to know the area under the curve which can be obtained numerically or by integration if $P$ is given as a function of volume.

One such relationship is known as the Ideal Gas Law. Historically it can be arrived at from experimental evidence but it can also be derived using a statistical mechanics approach. It is called an equation of state because it describes the relation among the macroscopic variables of the system ($P$, $V$, $T$) at an equilibrium state. Thus these variables $P$, $V$, $T$ are called state variables.

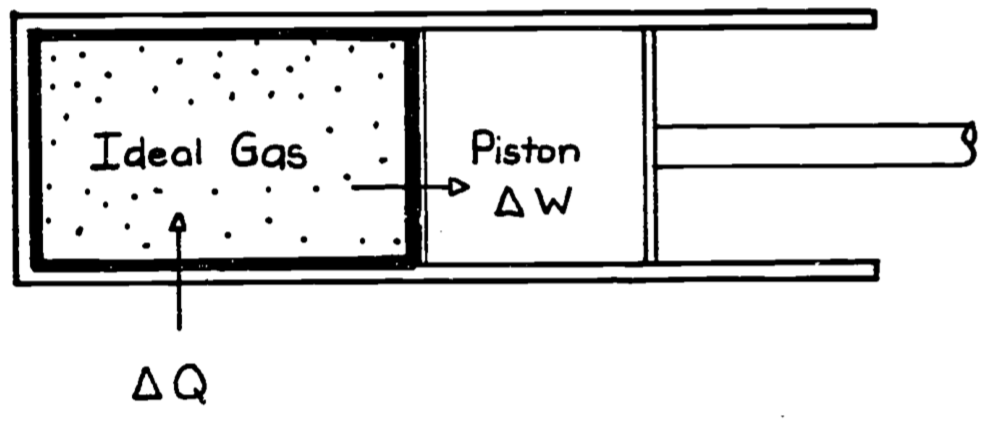
$Ideal gas contained in a piston chamber. $\Delta Q$ will be zero if the wall surrounding the system is perfectly insulated (adiabatic). $\Delta W$ represents the change it work accomplished by moving the piston.$

Figure 5.3: Ideal gas contained in a piston chamber. $\Delta Q$ will be zero if the wall surrounding the system is perfectly insulated (adiabatic). $\Delta W$ represents the change it work accomplished by moving the piston.

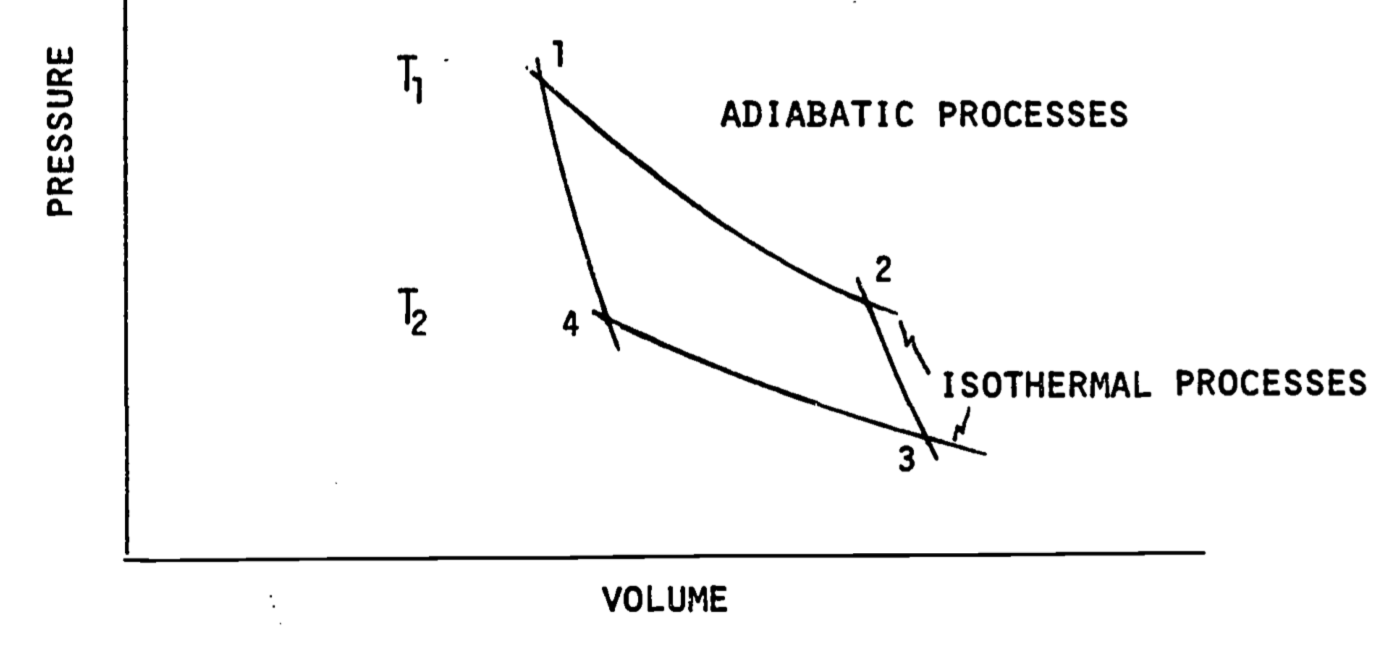
Pressure-volume diagram. A cycle is composed of going from 1 to 2, 2 to 3 and so on back to 1. When the cycle is composed of isothermal and adiabatic processes it is called a Carnot Cycle. Other cycles can involve constant pressure or constant volume steps. Note that $T_1$ is greater than $T_2$.

Figure 5.4: Pressure-volume diagram. A cycle is composed of going from 1 to 2, 2 to 3 and so on back to 1. When the cycle is composed of isothermal and adiabatic processes it is called a Carnot Cycle. Other cycles can involve constant pressure or constant volume steps. Note that $T_1$ is greater than $T_2$.

The Ideal Gas Law is \[\begin{equation} PV = nRT \tag{5.6} \end{equation}\] where $R$ is the gas constant which depends on the particular gas being considered (8.314 joules mole^-1 K^-1 for the ideal gas), $n$ is the number of moles, and the other variables are as above.

To complete our discussion of the piston example we need to examine several specific cases of the First Law. If the system is perfectly insulated then $Q$ is zero and the First Law becomes \[\begin{equation} \Delta U = -W \tag{5.7} \end{equation}\]

This is called an adiabatic process. Here since the internal energy is a function of state then the work done will also just depend on the end points and not the path.

If we wish to consider an ideal gas, the change in internal energy with respect to volume at constant temperature is zero so \[\begin{equation} dU = C_V d T \tag{5.8} \end{equation}\] Thus the First Law becomes \[\begin{equation} C_V d T = \delta Q - PdV \tag{5.9} \end{equation}\] If eq. (5.9) applies then it is possible to calculate $\Delta U$, $Q$ and $W$ for any path. $W$ can be evaluated numerically, $\Delta V$ can be calculated from the change in temperature (from the Ideal Gas Law) and $Q$ is gotten by subtraction.

These equations are not directly applicable to ecological systems but they help give an understanding of the First Law and provide a foundation for understanding heat engines and the Second Law of Thermodynamics.

In this introduction to thermodynamics we have tried to stimulate the reader’s interest by illustrating with biological examples the importance of the heat energy and mass balance of organisms. The basic thermodynamic terminology and the First Law are presented as a basis for other modules in the thermodynamics series. Examples of how these concepts are applied are found in the next module titled “Applications of the First Law to Ecological Systems.” The bibliography should help the reader to explore the importance of thermodynamics in ecology.