12.5 Heat Loss by Convection

We can then return to heat flow between the sheep and the external environment to calculate heat exchange via convection with the air. The sheep exchanges heat with the surrounding air at a rate determined by the temperature difference between the surface of the animal \(T_h\) and the air \(T_a\). The rate is also determined by the sheep’s surface area exposed to the air, which we approximate here the surface area of the animal at the fleece tips \(A_h\). Convection can be estimated as follows \[\begin{equation} H= H_L A_h(T_h-T_a) \tag{12.15} \end{equation}\] where \(H_L\) is a convective heat transfer coefficient (\(W m^{-2}K^{-1}\)). \(H_L\) is related to the boundary layer thickness and depends on whether the heat exchange is free or forced. The variables involved in heat transfer can be combined into dimensionless groups that are used to compare the scales of heat exchange processes and thus whether modeling free or forced convection is more appropriate. The Nusselt number (Nu) provides a dimensionless estimate of conductance as is estimated as \(Nu = H_L \times d / k\), where \(H_L\) is the convective heat transfer coefficient (\(W m^{-2} K^{-1}\)), \(d\) is the characteristic dimension (\(m\)), and \(k\) is thermal conductivity (\(W K^{-1}m^{-1}\)).

Since Nu is a function of boundary layer thickness, it clearly depends on the Reynolds number, which, it will be recalled, may be written \[Re =\frac{vd}{\nu} \] In this expression \(v\) \((m s^{-1})\) is the velocity of the fluid relative to the body and \(\nu\) is the kinematic viscosity of the fluid, about \(1.5 \times 10^{-5} m^2 s^{-1}\) for air at 20°C. Tables for Nu are provided in various texts on heat transfer. For gases, the empirical formula \(Nu = a Re^n\) may be used (Goldstein, 1938). The coefficient \(a\) and the exponent \(n\) vary considerably with the Reynolds number. Monteith (1973) provides the following table for cylinders whose axes are at right angles to the wind:

Re	Nu
\(1-4\)	\(0.89Re ^{0.33}\)
\(4-40\)	\(0.82Re^{0.39}\)
\(40-4\times10^3\)	\(0.63Re^{0.47}\)
\(4\times10^3-4\times10^4\)	\(0.17Re^{0.62}\)
\(4\times10^4-4\times10^5\)	\(0.024Re^{0.81}\)

To obtain some feeling for the magnitude of the convective term \(H\), let us assume that our wind speed is \(v = 2.0 m s^{-1} = 4.5 \mbox{ miles } hr^{-1}\). Then \(Re = (2.0)(0.5)/(1.5\cdot10^{-5}) = 6.67\cdot 10^4\), and we calculate \(Nu = (0.024)(6.67\cdot10^4)^{0.81}= 194\). The thermal conductivity \(k_a\) of air at 20°C is approximately \(2.57\cdot10^{-2} W m^{-1}°C^{-1}\), and since the surface area \(A_h\) of the sheep is \(5\pi\cdot10^{-1}m^2\),

\[\begin{align*} Nu &= H_L \cdot d / k\\ 194 &= H_L \cdot 0.5 / (2.57 \cdot 10^{-2})\\ H_L &= 10\\ H&= H_L A_h(T_h-T_a)\\ H&= 10 \cdot 5\pi \cdot 10^{-1}(25-10)\\ H&=235 W \end{align*}\] assuming \(T_h\) = 25°C and \(T_a\) = 10°C.

The temperature profile associated with convection is depicted in Figure 12.2.

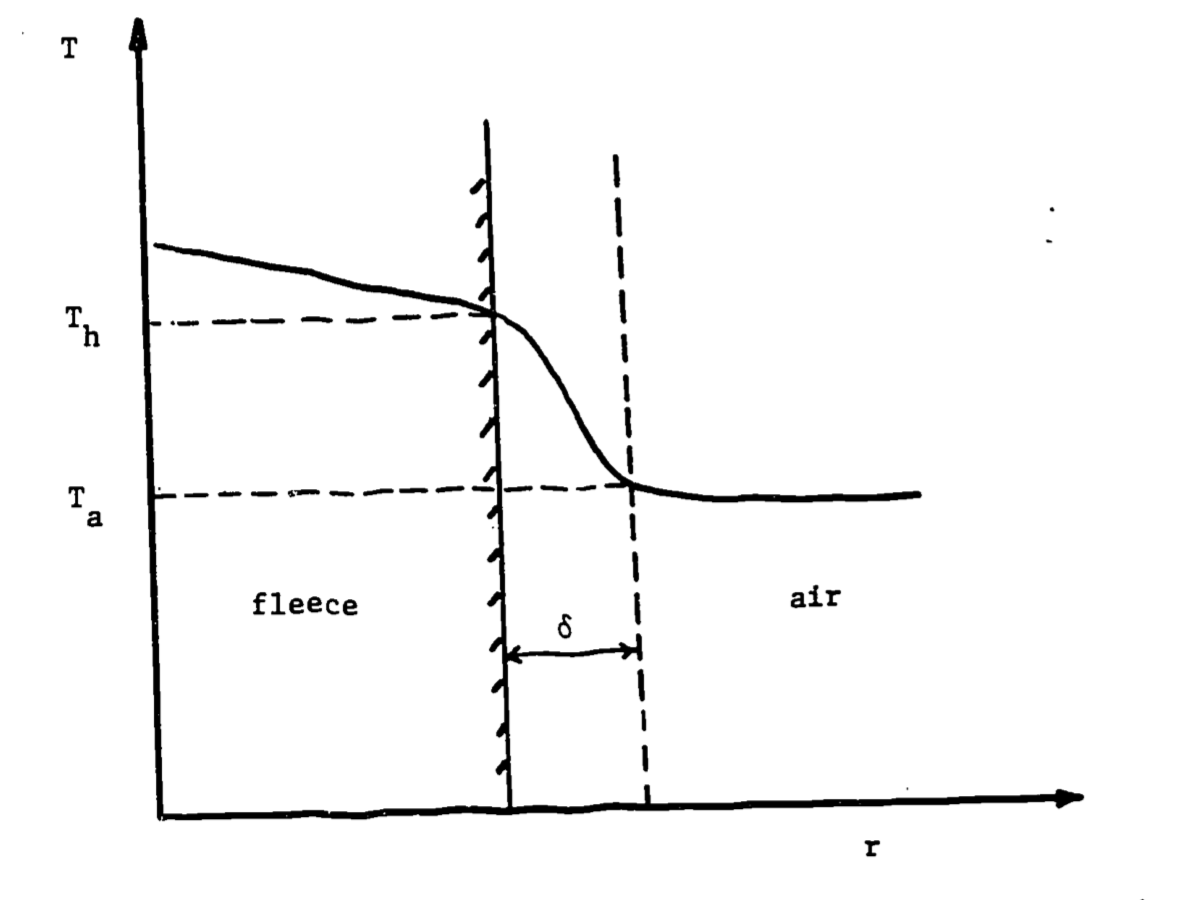
Figure 12.2: Temperature profile across fleece and air. Delta represents boundary layer thickness, \(T_h\)=fleece-tip temperature, \(T_a\) = air temperature.

It is also possible to calculate the heat lost by “free convection,” which is important when wind speed is less than \(1 m s^{-1}\). In this case, the buoyancy of heated air is a dominant factor in the transfer of heat away from the animal. Calculation of \(H\) in this “unstable” case involves determination of the “Grashof number,” which must be used in place of the Nusselt number. A problem involving free convection is offered as one of the exercises for this module.