14.3 Description of Turbulence
What is turbulence? Perhaps the only generally agreed upon response to this question is that turbulence is difficult to define! Generally, the answer takes the form of a list of the characteristics of turbulent flows, such as is done by Lumley and Panofsky (1964, p.3 ff) and Tennekes and Lumley (1972, p.1 ff). Campbell (1977) presents a more elementary discussion of two of these characteristics, probably the easiest to conceptualize, while still conveying the ideas important for this discussion: variability and diffusivity.
14.3.1 Variability
Anyone who has observed the plume from a smokestack and noticed the irregularity of the force of the wind on a gusty day, or simply lain on their back and witnessed the random evolution of a cumulus cloud, has an appreciation of the variability of turbulence. For example, consider the wind record of Fig. 14.1. It gives three one-minute records of the elevation angle from a bidirectional wind vane. Such a wind vane can rotate in the horizontal plane (azimuth) as well as around a horizontal axis perpendicular to the mean wind (elevation). Notice that only a total of seven minutes has elapsed from the first to the last record. The intermittency of the turbulence is illustrated by the marked difference between the record from 1337-1338 and the other two.
Consider the problem of predicting the motion of atmospheric contaminants such as pollen, fungal spores, or pollutants with such variable winds. If the time period of interest is short, the analysis can indeed become difficult.
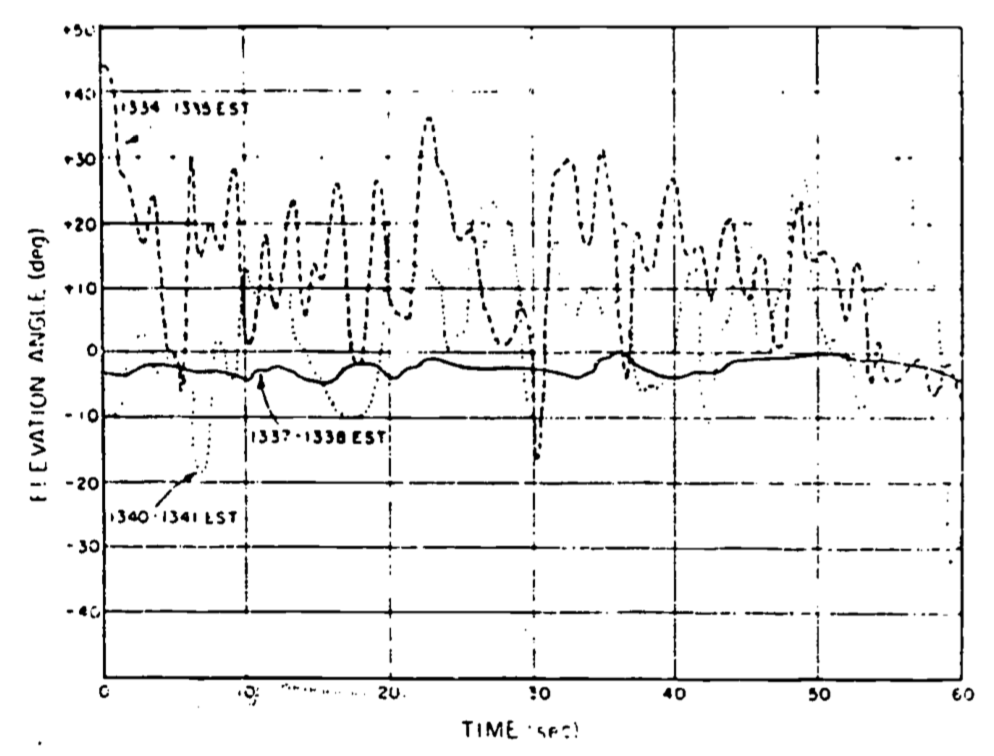
Figure 14.1: Bidirectional vane record of elevation for three one-minute perioes on July 19, 1962 at Douglas Point, Canada.
The obvious problem is how to quantify something that is, in effect, unpredictable. The answer lies in the use of statistical methods. Fortunately, it turns out that detailed information on the flow field is not necessary, and such simple methods as utilizing time averages of the quantities of interest will suffice in many cases, provided sufficient averaging time is allowed. This is fortunate for another reason. As discussed briefly by Cowan (1979a) (and more completely by Tennekes and Lumley (1972)), equations of motion do exist which in general describe the motion of any fluid. However, the solutions to these equations appear to be so sensitive to minute changes in a given set of experimental conditions that one could never measure these conditions in sufficient detail to permit detailed prediction of the flow (Lumley and Panofsky 1964). In mathematical parlance, this difficulty is caused by the high degree of nonlinearity in the set of partial differential equations applicable. This results in the solution being very sensitive to the given set of conditions (i.e., the boundary conditions).
Turbulence is variable in space as well as time. Campbell’s (1977) examples of fields of “waving grain” or “cat’s paws” on a lake point this out particularly well.
In fact, this variability in both space and time is quite large. Campbell (1977) illustrates the extremes of these temporal and spatial scales by comparing wind gusts large enough to shake a house to the very small scale “heat waves” that can be observed over a hot surface such as an asphalt highway on a hot day. This large variation in the scales of turbulence has two important consequences. First, one must be cautious when making the analogy between turbulent and molecular transport (diffusion). This problem will be treated later in the discussion of diffusivity. Second, there is the practical problem of the limits imposed by the finite (computational) speed of computers.
Notwithstanding the fact that the equations of motion (known as the Navier-Stokes equations) are extremely sensitive to their boundary conditions, their solution is still difficult for problems in atmospheric turbulence due to the wide range of scales involved. As an illustration, consider the complexity of one of the simplest problems: channel flow. Figure 14.2 illustrates a channel of infinite horizontal dimension and of height H=15 cm, with a fluid moving from left to right with a maximum velocity \((u)\) of \(1 m s^{-1}\).
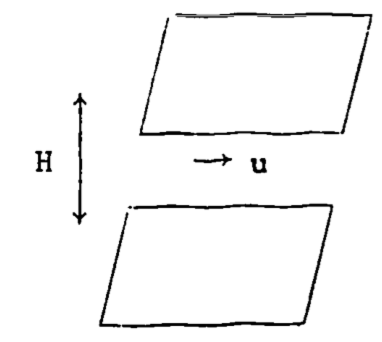
Figure 14.2: Fluid movement in an infinite channel.
Suppose one is required to solve the equations of motion for the velocity and pressure fields. The given dimension and the velocity will give a Reynolds number (\(Re\)) of \(\sim10^4\). The Reynolds number is discussed more fully in the section on the origins of turbulence, so it will suffice to say here that it is a general indicator of whether a flow is turbulent. \(Re\) is defined as \[Re = \frac{ud \rho}{\mu}\] where \(u\) is velocity, \(\rho\) density and \(\mu\) is the dynamic viscosity of the fluid, and \(d\) is a characteristic dimension of the flow. In this example, then, \[ Re = \frac{1m\:s^{-1} \times 0.15m \times 1.2 kg\:m^{-3}}{0.18 \times 10^{-4}kg\:m^{-1} s^{-1}} = 10^4\] which indicates a well-developed turbulent flow.
To estimate the computational effort involved here, one must resolve the largest and smallest eddies (turbulence scales) in the flow. Turbulence theory (see Tennekes and Lumley 1972, p. 21) tells us that the ratio of the large to small eddies will be proportional to \((Re)^{3/4}\) . If we designate the size of the small-scale eddies as \(n\), we can write this ratio as \[\frac{H}{n} \sim (Re)^{3/4} = 1000\] It turns out that there are four equations of motion, which are nonlinear and thus require a numerical solution technique such as finite differences. In turn, this necessitates that a grid network be set up in three dimensions, and the equations solved simultaneously at each point. The number of grid points necessary in both directions perpendicular to the flow will be 2000, assuming two points are required to define an eddy. In the direction of flow, the eddy size would not thus be limited, so we’ll assume 20,000 are required. Hence the number of grid points equals \(2000 \times 2000 \times 20000 \approx 10^{11}\). Assuming the four motion equations with four unknowns require at least 102 operations per grid point, then the total number of operations per time step would be equal to \(10^2 \times 10^{11} = 10^{13}\) . If a minimum of \(10^2\) time steps are required to obtain a meaningful solution, the total number of operations necessary becomes \(10^{15}\).
Although the numerical solution to the turbulence problem present a computational challenge, this should not be viewed by the biologist as an entirely negative result. In fact, the semi-empirical approach (as pointed out in the Introduction) is in many ways more suited to the type of analysis likely to be needed by, say, a physiologist or ecologist. Consider the various energy budgets involved in the examples of Stevenson (1979b). All that is required in the stream flow, leaf, or spider example is a reliable estimate of the various fluxes of energy; details about how these fluxes occur are secondary. However, this should not be taken to minimize the importance of more detailed characteristics of turbulent flow fields in other cases of biological interest. Examples of this latter case include nutrient diffusion to plankton, location and size of stream insects, mobility and habitat of flying insects, aerosol dispersion, leaf shapes and characteristics, and even bird wing shape. Ultimately, it is important that the biologist should at least realize the general nature of the problem of turbulent flow as a prerequisite to determining the proper mix of analytic and empirical methods.
14.3.2 Diffusivity
“The outstanding characteristic of turbulent motion is its ability to transport or mix momentum, kinetic energy, and contaminants such as heat, particles, and moisture” (Tennekes and Lumley 1972, p. 9). Without turbulent transport, life on the earth would either suffocate due to the slow rate of diffusion of CO2 or O2 from the upper layers of the atmosphere or be poisoned by the buildup of pollutants near the surface. This is well illustrated by a simple example taken from Monteith (1973, p. 134). The amount of CO2 required by a healthy crop canopy over the course of a day is equivalent to all the CO2 in the first 30m of the atmosphere. The actual diurnal variation of CO2 concentration in this layer rarely exceeds 15% of the mean concentration. These figures suggest turbulent transfer supplies CO2 from as high as \(30m/0.15= 200m\). In fact, measurements have detected small diurnal fluctuations as high as 500m. Apparently, a relatively rapid means of transport must be supplying CO2 from above the surface layer to the plants.
To understand more fully why turbulence has such effective mixing properties, it is useful to compare turbulent exchange with the other mode of exchange important in transport processes, that of molecular diffusion (see also Cowan 1979b or Tennekes and Lumley 1972). Molecular diffusion is a mixing process dependent upon exchange at the molecular level. Consequently, its characteristic length scale is the mean free path between molecular collisions, typically \(7 \times 10^{-8}m\) for air at room temperature and pressure. Since the root mean square velocity for air molecules under similar conditions is approximately \(480m s^{-1}\) , the characteristic time scale is quite small (\(7 \times 10^{-8}m /480m s^{-1} = 1.5 \times 10^{-10} s\)). Even though the interactions (collisions) are quite frequent, the small characteristic lengths over which they act tend to diffuse properties with large scales relatively slowly. (As an example of a property with a large scale, one might consider heat exchange between the warm ground and cooler atmosphere, typically up to heights of 1 kilometer on a warm, sunny day.) As implied in our earlier example of channel flow, the characteristic exchange length (scale) for turbulent exchange is limited only by the dimension of the flow boundaries. Consequently, in the lowest 30m or so of the atmosphere (the surface layer), the characteristic exchange length for the transport at a particular height \(z\) will be of the order of \(z\). This is because the basic unit of exchange for turbulent flow is what is commonly termed an “eddy,” which may be envisioned as a parcel of air in rotational motion which tends to retain its identity and remain relatively intact for a finite distance and time, In other words, we simply consider the random motion of “bunches” of molecules rather than that of individual molecules. The result is mass transport of such quantities as heat over distances of the same order as the size of the eddy, a scale obviously much larger than that in molecular diffusion. More will be said about eddies later on in this section.
A simple example based on Tennekes and Lumley (1972) illustrates the extremely diffusive nature of turbulence by contrasting it with molecular diffusion. Consider the cross-sectional diagram of a room in Fig. 14.3, with a radiator in one corner. The question is posed, “How long will it take to heat the room?” The answer, besides clarifying what we mean by diffusivity, gives several insights into common “tricks of the trade” in turbulence theory.
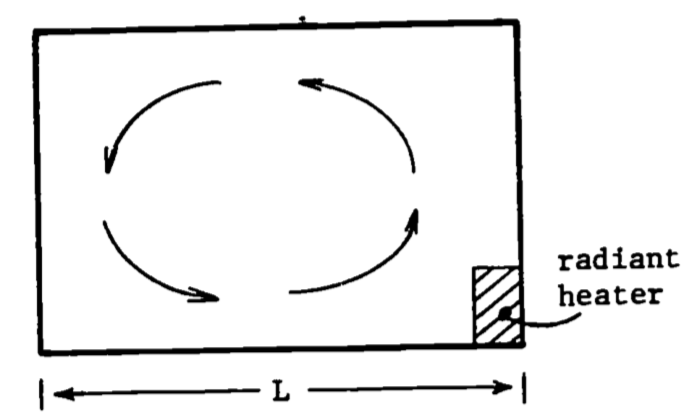
Figure 14.3: Convection currents.
The first step in tackling this problem will be to make some appropriate simplifying assumptions. Assume for the moment that gravity is ignored so that no convective currents (such as illustrated in Fig. 14.3 will be produced. Consequently, heat transfer is possible only through molecular diffusion. This process is governed by a diffusion type equation (Simpson 1979, or Tennekes and Lumley 1972) of the sort \[\frac{\partial \theta}{\partial T} = \gamma \nabla^2 \theta\] where \(\theta\) is temperature, \(T\) is time, \(\gamma\)is thermal diffusivity, and \(\nabla^2\) is the Laplacian operator.
The second step is to decide to obtain an order of magnitude (within a factor of 10) estimate, rather than attempt the difficult task of obtaining an exact detailed solution. Consequently, we will employ the tools of dimensional analysis (see Fletcher 1979 or Vennard and Street 1975) to interpret the diffusion equation dimensionally as \[\frac{\partial \theta}{ T} \sim \gamma \frac{\nabla \theta}{L^2}\] Rearranging terms, one obtains an expression for the time scale \(T_m\) of the molecular diffusion, \[\begin{equation} T_m \sim \frac{L^2}{\gamma} \tag{14.1} \end{equation}\] Notice that all diffusion processes are governed by this relation, where the diffusivity relates a penetration distance to a time independent of the quantity being diffused (notice that \(\theta\) cancels out). The dimensions of diffusivity are always (\(L^2 /T\)). In the present example with \(L=5m\) and \(\gamma = 2 \times 10^{-5} m^2 s^{-1} , T_m \sim 1.25 \times 10^6 s\) or about 14 days. Such a long characteristic time scale compared with the time actually required to heat a room indicates that some other transfer process must be operating.
Removing the first simplifying assumption and allowing for the presence of gravity leads to the weak convective circulation indicated in Fig. 14.3. The heating of the radiator induces density differences in the air that when acted upon by gravity cause “the hotter air to rise and the cooler air to sink,” so that the circulation illustrated is not unexpected. Therefore, using dimensional analysis of the convective velocity in the room (\(U_c\)); a characteristic time for turbulent diffusion can be expressed as \[\begin{equation} T_t \sim \frac{L}{U_c} \tag{14.2} \end{equation}\] Notice that the dimensions of a length divided by velocity is a time. It is assumed that the length scale of the turbulent motion in the air is characterized by the length \(L\). It certainly is no larger, and it seems reasonable that the large eddy (illustrated by arrows in Fig. 14.3 will be most effective in transport. It remains to estimate the convective velocity \(U_c\). Experience suggests that it must be small, somewhere on the order of \(U_c=0.05 m s^{-1}\) (see Tennekes and Lumley 1972). Then \(L=5m\) implies a \(T_t\) of about \(100 s\), In conclusion, it is clear that turbulence is much more efficient than molecular diffusion in the transport of quantities such as heat.
The considerations discussed in the example of the heating of the air in the room can be extended to the situation in the atmosphere. It should be made clear that the eddy sizes in the atmosphere, or in the room, are limited in size by the flow boundaries. This only sets the upper limit, albeit the most efficient for transport, as illustrated below. Actually, a whole range of smaller eddy sizes exists, until they become so small that molecular forces become significant. The turbulent structure in the atmosphere in simplest terms can be envisioned as a whole series of eddies, such as in our room example, being carried along by the mean wind, \(\overline U(z)\) (Fig. 14.4).
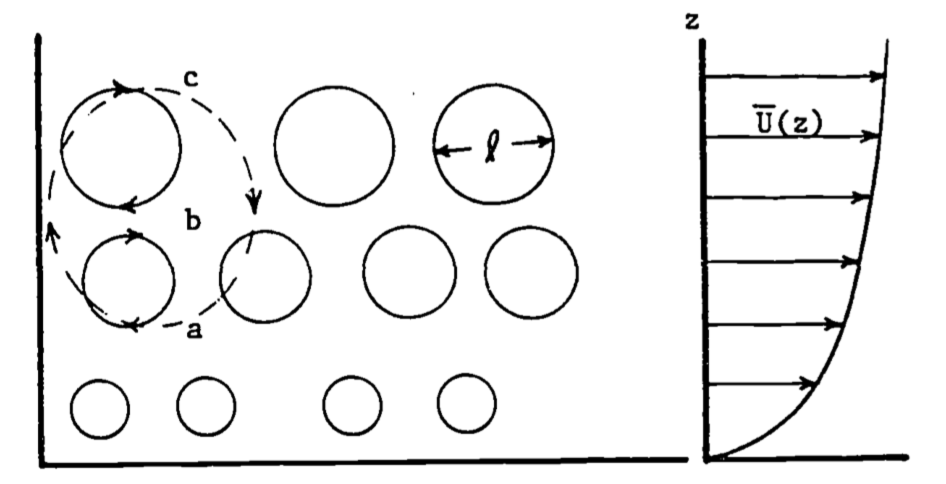
Figure 14.4: A range of eddies exists, with mean diameter k proportional to height z.
Notice that as height (\(z\)) increases, the eddies tend to become larger, since the surface interferes less with the circulation. Also notice that in the transference of some property, e.g., a warm air parcel, from point A to C, the larger eddy will be the most efficient. This is because the larger eddy transports the quantity of interest from A to C directly, avoiding the more circuitous route and extra mixing that transfer by smaller eddies entails. This latter concept is treated again in the section on K-theory.
Consider the following simple example which (1) illustrates the use of the proper statistical measures for dealing with the variability of a turbulent flow, (2) points out an interesting use of the eddy concept in dealing with turbulent diffusivity, and (3) is a good example of a case where detailed knowledge of the turbulent flow structure is critical to solution of a biological problem.
An important area of pulmonary research concerns the oxygenation of pulmonary capillary blood. The factors that control this process are of obvious importance, especially in the understanding and treatment of various lung diseases. Briefly, the oxygen must cross the alveolar-capillary membranes from the Ling air spaces, diffuse through the blood plasma, pass through the blood cell membrane, diffuse through the cell interior, and finally react chemically with the hemoglobin. Previously, it was assumed that the alveolar-capillary membrane was responsible for most of the resistance to oxygen diffusion. More recently, the turbulent flow properties of dilute suspensions of red blood cells in small diameter tubes have been used to study the resistance due to the cell membrane, interior, and reaction rates. The premise of most of this research was that, since the flow was thought to be turbulent, mixing of the red blood cells with the suspending medium would be quite rapid. Consequently, it followed that an unmixed fluid layer relatively depleted of oxygen would not exist, and hence would not contribute to the diffusion resistance.
Carisen and Comroe (1958), by heat treatment of red cells, obtained a spherical-shaped cell of identical volume to the normal disk-shaped cell. They found oxygen uptake to be the same for both shapes using the flow apparatus, indicating that increasing the diffusion path length inside the cell has no effect. Furthermore, the reaction rate of oxygen with hemoglobin is ruled out as a factor by the comparison of oxygen and nitric oxide uptake, the latter of which reacts ten times as fast as the former with hemoglobin. Again, no change in diffusion time was found by Carlsen and Comroe. Based on the assumptions of turbulent flow and complete mixing, they concluded that the red cell membrane was the chief source of resistance. However, other investigators (e.g., Kreuzer and Yahr 1960) have compared the uptake rates of similar layers of red cells and plain hemoglobin. Again, uptake rates were the same, which apparently rules out the cell membrane as the source of resistance. Which conclusion is in error?
Gad-el-Hak et al. (1977) have proposed an answer to the dilemma from an analysis of the relevant turbulent properties of the flow fields involved. They first of all clarify the criteria for true turbulent flow in such studies (\(Re>3000\)). Evidence is then provided which indicates that, contrary to previous thought, an unmixed fluid layer does exist next to the cell. This can, of course, explain the aforementioned conflicting results. Envision, if you will, a typical blood cell, being tossed and whirled about by the turbulent fluid. This cell takes up oxygen, causing an area of oxygen deficit in its immediate vicinity. The replenishment rate is dependent primarily upon the size of the eddies and the length of time they exist relative to the distance and time dependence of oxygen uptake by the cells. For example, if the eddies are large relative to the cells, the cell will tend to move along with the eddy. This circumstance tends to deplete the eddy of oxygen, while at the same time not allowing the cell to come into effective contact with other more oxygen rich eddies. Conversely, if the eddies are small relative to the cell, the cell will tend to contact eddies more often, perhaps several at a time. Hence, mixing is more effective, and diffusion resistance is smaller. A further discussion of such time dependent phenomena is contained in Problem 5.
Further evidence to support this explanation was obtained by Gad-el-Hak et al. through the use of sophisticated laser anemometry techniques to measure the turbulent fluctuations, and various statistical measures to quantify eddy sizes and velocities. (Details are not covered in this paper. See Gad-el-Hak 1977 or Tennekes and Lumley 1972 for further discussion.) In essence, their results show that the turbulent scales range from \(0.07 mm\) to \(1.3 mm\), as compared to the \(0.008 mm\) dimension for a red blood cell. Their analysis indicates 45 milliseconds (\(ms\)) are required, on the average, to replenish the oxygen in the layer immediately around the cell. This compares to independent measurement which indicates that the uptake process requires \(10-100 ms\). Both time and scale considerations thus are shown to lend support to their hypothesis that O2 uptake is at least partly limited by convective mixing in the layer of fluid immediately adjacent to the cell wall.