8.12 Problemas relacionados con el $p$-valor y el nivel de significación

En el siguiente artículo del periódico digital El Confidencial podemos leer

“Los investigadores no saben estadística (y eso perjudica a la ciencia)”

En el interior de la noticia, podemos leer que

“la estadística es la herramienta más importante de que dispone la ciencia para confirmar o refutar hipótesis. Ahora, investigadores denuncian que su uso incorrecto, por mala fe o ignorancia, amenaza la calidad de la investigación. El culpable de todos los males es el $p$-valor, un término estadístico cuya popularidad ha aumentado con los años al mismo ritmo que su mal uso.”

Más adelante, comenta

“Un estudio publicado esta semana en la revista ‘JAMA’ ha revisado”millones" de estudios biomédicos fechados entre 1990 y 2015 para concluir que la ‘mala estadística’ es cada vez más empleada. “El $p$-valor ya es una técnica subóptima, y si encima se usa de una forma sesgada puede ser muy confusa”, asegura el director del Centro de Investigación Preventiva de la Universidad de Stanford y autor principal del estudio, John Ioannidis."

Cualquier interesado, a estas alturas, ya ha acudido a la fuente original y leído el artículo entero. Vamos a tratar en las siguientes líneas de aclarar algunas de los problemas que puede presentar el $p$-valor (si no se utiliza correctamente).

Hemos visto que el test $t$ para la media de una muestra utiliza el estadístico $$T=\frac{\bar{x}-\mu _{o}}{\hat{S}_{n-1}/\sqrt{n}}\ \ \in \ \ t_{n-1}.$$

A partir de una muestra, calculamos la media muestral $\bar{x}$, la cuasi-desviación típica muestral $\hat{S}_{n-1}$ y hacemos la cuenta: $$T=\frac{\bar{x}-\mu _{o}}{\hat{S}_{n-1}/\sqrt{n}}=\sqrt{n}\cdot \frac{\bar{x}-\mu _{o}}{\hat{S}_{n-1} }$$ En muchas ocasiones, si se pretende probar, por ejemplo, si un nuevo tratamiento es eficaz, el contraste es de la forma $H_0: \mu = 0$ frente a $H_1: \mu \neq 0$, ya que obtendremos una muestra de pacientes y mediremos una variable antes de efectuar el tratamiento (dolor, temperatura, horas de sueño… ) y después de realizar el tratamiento. Si el tratamiento es efectivo las diferencias de los valores antes y después serán diferentes a cero (el dolor ha disminuido, o la temperatura, o las horas de sueño han aumentado…).

En este caso el estadístico $T$ es $$T=\frac{\bar{x}-0}{\hat{S}_{n-1}/\sqrt{n}}=\sqrt{n}\cdot \frac{\bar{x}}{\hat{S}_{n-1} }$$ Si el tamaño de la muestra es grande, este valor también lo va a ser (puesto que se supone que, tomando muestras diferentes, la media y la cuasi-desviación típica muestral nos darán siempre valores parecidos). Es decir, el valor de $T$ aumenta con el tamaño de la muestra, y recordemos que el $p-$valor es el área a la derecha del valor T (o dos veces ese valor). Esto significa que el $p-$valor va a ser próximo a cero, y la hipótesis nula siempre se va a rechazar.

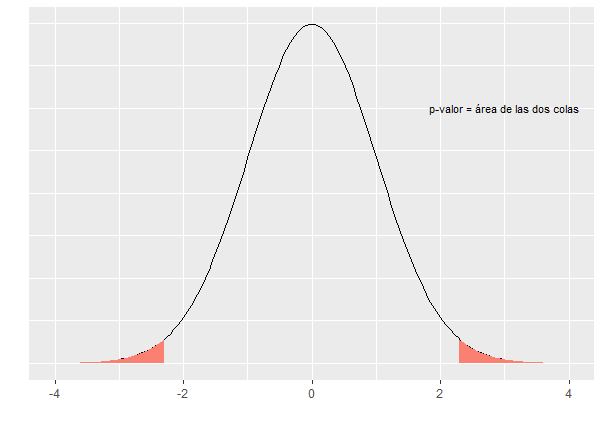
Figura 8.3: $p$-valor para un test t bilateral.

La conclusión es que, para demostrar que un tratamiento es efectivo, no es necesario que lo sea, sino simplemente hay que hacer un ensayo clínico con un tamaño de muestra lo suficientemente grande.

Esto ocurre porque el test de hipótesis mide la diferencia entre la media muestral $\bar{x}$ y el valor cero. Cuando el tamaño de la muestra es muy grande, es como si dispusiésemos de toda la población, con lo cual cualquier diferencia de $\bar{x}$ con el valor cero se hace significativa (tenemos toda la población y queremos saber si la media es cero. Si obtenemos un valor distinto de cero, aunque sea muy poco distinto, rechazaremos que sea cero).

En su libro Métodos estadísticos para investigadores (Fisher 1992), Ronald Fisher escribió:

“Personally, the writer prefers to set a low standard of significance at the 5 percent point… A scientific fact should be regarded as experimentally established only if a properly designed experiment rarely fails to give this level of significance”

“Un hecho científico se considerará probado experimentalmente sólo si un experimento correctamente diseñado raramente falla en dar este nivel de significación. Un cinco por ciento significaría que el experimento debería repetirse y, de cada cien repeticiones, debería arrojar valores significativos en, al menos, 95 de cada 100 veces”. De esta manera quedaría demostrado que los efectos observados no serían a causa del azar. En definitiva, un $p-$valor más pequeño de 0.05 haría al experimento digno de atención, y debería repetirse para tener más certeza sobre el mismo.

El problema surge cuando un experimento es costoso o involucra seres humanos, con todos los problemas añadidos (posibles efectos secundarios, dificultad de repetición… ). Paulatinamente, se realizaron experimentos donde se obtenía un $p-$valor. Y había que tomar una decisión. Estamos hablando de la primera mitad del siglo XX, cuando no había ordenadores ni programas que calcularan nada. Lo que había eran tablas estadísticas para poder discernir si el $p$-valor era mayor o menos a algún nivel determinado. Se fijaron tres valores fundamentales: $\alpha=0.1, 0.05$ y $0.01$. Por aquello de estar en el medio, el nivel $\alpha=0.05$ fue el más utilizado. De manera que, si el $p-$valor era menor que 0.05 se rechazaba la hipótesis nula, y el tratamiento es efectivo. Si el $p-$valor era mayor o igual, no se podía rechazar la hipótesis nula, y por lo tanto el tratamiento no podía aceptarse como efectivo.

Esta claro que si, por ejemplo, se pone el límite de significación en 0.05, estamos afirmando que, sobre la base de que 95 veces sobre 100 esperaríamos encontrar que el tratamiento es efectivo. Pero si obtenemos $p=0.06$ entonces ocurre que 94 de cada cien veces esperaremos encontrar que el tratamiento es efectivo. ¿Es tanta la diferencia?

Lo que ha sucedido, históricamente, es lo que se llama el sesgo de publicación. Si un tratamiento resulta efectivo, es mucho más probable que sea merecedor de ser publicado en una revista científica que si no resulta efectivo. De ahí que se hayan visto todo tipo de artílugios para conseguir que un $p$-valor consiga que un tratamiento sea efectivo. Si en el experimento se obtuvo $p=0.049$ se dice $p<0.05$ y punto. Si no se obtuvo un valor menor que 0.05, se intenta conseguir un tamaño de muestra lo suficientemente grande para que cualquier diferencia resulte significativa (y digna de mención en alguna revista científica).

Ya en 1994, el famoso psicólogo y estadístico Jacob Cohen (1923-1998), conocido por sus estudios del tamaño del efecto y otros trabajos que ayudaron a sentar las bases para los metaanálisis, publicó un artículo enormemente citado: The earth is round (p<.05), cuyo abstract, traducido, viene a decir:

“Tras cuatro décadas de severa crítica, el ritual del contraste de hipótesis (NHST) —decisiones mecánicas y dicotómicas alrededor del sagrado criterio del 0.05— todavía perdura. Este artículo repasa los problemas derivados de esta práctica, incluyendo la casi universal malinterpretación del $p$-valor como la probabilidad de que $H_0$ sea falsa, la malinterpretación de su complementario como la probabilidad de una réplica exitosa y la falsa premisa de que rechazar $H_0$ valida la teoría que condujo a la prueba. Como alternativa, se recomiendan el análisis exploratorio de datos y los métodos gráficos, la mejora y la estandarización progresiva de las medidas, el énfasis en la estimación de los tamaños de los efectos usando intervalos de confianza y el uso adecuado de los métodos estadísticos disponibles. Para garantizar la generalización, los psicólogos deben apoyarse, como ocurre en el resto de las ciencias, en la replicación.”

En la decimotercera edición de Métodos estadísticos para investigadores, Fisher realizó la siguiente aclaración sobre los $p$-valores:

“el $p$-valor indica la fuerza de la evidencia contra la hipótesis nula… y los contrastes de significación deben utilizarse como ayuda para el juicio, y no deben confundirse con pruebas de aceptación automática, o funciones de decisión.”

En 2016, la American Statistical Association (ASA) publicó una declaración sobre los $p$-valores, elaborada por un grupo de más de dos docenas de expertos (Wasserstein, Lazar, and others 2016). Aunque hubo discusiones controvertidas sobre muchos temas, el informe de consenso de la ASA incluye la siguiente declaración: “El uso generalizado de la’significación estadística’ (generalmente interpretada como $p < 0.05$) como una licencia para hacer una afirmación de un hallazgo científico (o verdad implícita) conduce a una considerable distorsión del proceso científico”

Además, un grupo de siete estadísticos de la ASA publicó en European Journal of Epidemiology (Greenland et al. 2016) una extensa revisión de $25$ malas interpretaciones de los $p$-valores, los intervalos de confianza y la potencia estadística, cerrando con las palabras: “Nos unimos a otros para señalar la degradación de los $p$-valores en significativos y no significativos como una práctica estadística especialmente perniciosa”.

Algunos de los comentarios más relevantes inciden en que la significación estadística no puede tomarse como evidencia de que la hipótesis de investigación sea cierta; ni proporciona la probabilidad de la hipótesis, por lo que no hay base para estudiar la replicación y tampoco nos proporciona evidencias verificables de replicación.

Para evitar malas interpretaciones y ayudar en la toma de decisiones, muchos estadísticos sugieren utilizar el enfoque bayesiano, tanto en la realización de test estadísticos (test bayesianos) como en el cálculo de intervalos de confianza y el uso del factor de Bayes (Gelman et al. 2013), (Casella and Berger 1987).

8.12.1 Evidencia y descubrimientos en física

Como detalle de interés, resaltamos que, desde los años 90, los experimentos de física de partículas utilizan como como criterio el correspondiente a un $p$-valor de $2.87 \cdot 10^{-7}$, para refutar con seguridad una hipótesis nula. Solo en ese caso se habla de observación o descubrimiento. Este criterio se llama $5\sigma$, El criterio llamado $3\sigma$, correspondiente a un $p-$valor de $1.35\cdot 10^{-3}$, se utiliza para hablar de evidencia. Fuente: trabajo.

Hablando de forma más mundana, un nivel de significación $\alpha = 0.05$, que es de los más habituales en los artículos científicos, supone un criterio de $2\sigma$, que, recordemos que en una distribución normal (de media genérica $\mu$ y desviación típica $\sigma$), fuera del intervalo $(\mu -2\cdot \sigma, \mu +2\cdot \sigma)$ se encuentran los valores «más raros», que vienen a ser tan sólo un $5$ por ciento.

Realmente, no es un $5$ por ciento, sino un $4.55$ por ciento. Lo calculamos en una $N(0,1)$:

2*(1-pnorm(2))

## [1] 0.0455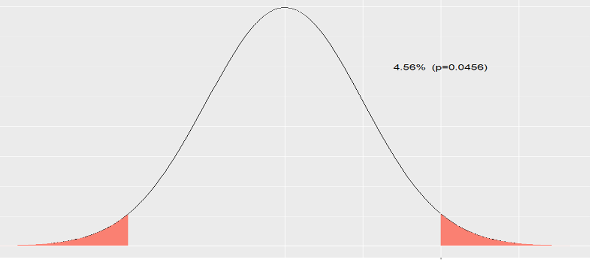

Figura 8.4: Área fuera del intervalo (-2,2).

Fuera del intervalo $(\mu -3\cdot \sigma, \mu +3\cdot \sigma)$ el área es

2*(1-pnorm(3))

## [1] 0.0027

Si lo dividimos por $2,$ nos da el valor $1.35\cdot 10^{-3}$, que es el que citan en el trabajo (es decir, que consideran el área a la derecha de $\mu + 3\sigma$).

Fuera del intervalo $(\mu -4\cdot \sigma, \mu +4\cdot \sigma)$

2*(1-pnorm(4))

## [1] 6.334e-05

y fuera de $(\mu -5\cdot \sigma, \mu +5\cdot \sigma)$

2*(1-pnorm(5))

## [1] 5.733e-07

que, al dividirlo por $2$, nos da, aproximadamente, $2.87 \cdot 10^{-7}$ (área a la derecha de $\mu + 5\sigma$).

Bibliografía

Casella, George, and Roger L Berger. 1987. “Reconciling Bayesian and Frequentist Evidence in the One-Sided Testing Problem.” Journal of the American Statistical Association 82 (397). Taylor & Francis: 106–11.

Fisher, Ronald Aylmer. 1992. “Statistical Methods for Research Workers.” In Breakthroughs in Statistics, 66–70. Springer.

Gelman, Andrew, Hal S Stern, John B Carlin, David B Dunson, Aki Vehtari, and Donald B Rubin. 2013. Bayesian Data Analysis. Chapman; Hall/CRC.

Greenland, Sander, Stephen J. Senn, Kenneth J. Rothman, John B. Carlin, Charles Poole, Steven N. Goodman, and Douglas G. Altman. 2016. “Statistical Tests, P Values, Confidence Intervals, and Power: A Guide to Misinterpretations.” European Journal of Epidemiology 31 (4): 337–50. doi:10.1007/s10654-016-0149-3.

Wasserstein, Ronald L, Nicole A Lazar, and others. 2016. “The Asa’s Statement on P-Values: Context, Process, and Purpose.” The American Statistician 70 (2): 129–33.