4.21 Problemas de paradojas

4.21.1 Problema de Monty Hall

En el siguiente video aparece la resolución del problema para quien no le apetezca leer:

La dinámica de un concurso de televisión es la siguiente: hay tres puertas y detrás de una de ellas está el premio; el concursante elige una de las puertas pero, antes de abrirla, el presentador, que sabe donde está el premio, abre una de las otras dos puertas, muestra que en ella no se encuentra el premio y, acto seguido, le ofrece al concursante una última oportunidad de cambiar la puerta elegida. ¿Qué debe hacer el concursante?

El Problema de Monty Hall es un problema de probabilidad que está inspirado por el concurso televisivo estadounidense Let’s Make a Deal (Hagamos un trato), famoso entre 1963 y 1986. Su nombre proviene del presentador, Monty Hall.

Figura 4.47: El presentador de televisión Monty Hall y su amiga.

En este concurso, el concursante escoge una puerta entre tres, y su premio consiste en lo que se encuentra detrás. Una de ellas oculta un coche, y tras las otras dos hay una cabra. Sin embargo, antes de abrirla, el presentador, que sabe dónde está el premio, abre una de las otras dos puertas y muestra que detrás de ella hay una cabra. Ahora tiene el concursante una última oportunidad de cambiar la puerta escogida ¿Debe el concursante mantener su elección original o escoger la otra puerta? ¿Hay alguna diferencia?

A primera vista, parece que da igual. La intuición nos dice que ahora, quitando una puerta sin premio, la puerta que nosotros escogimos tiene un 50% de tener una cabra y por tanto da igual cambiar que no hacerlo.
Desarrollamos todas las posibilidades:

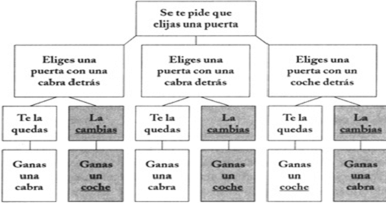
Figura 4.48: Casos posibles del problema.

Si miramos las posibilidades de éxito de cambiar o no cambiar, vemos que si no cambiamos tenemos 1/3 y si cambiamos tenemos 2/3.

Veamos cómo se hace con probabilidades condicionadas. Definimos los siguientes sucesos: \(A\)=“El jugador selecciona la puerta que contiene el coche en su selección inicial”. \(B\)=“El jugador selecciona una puerta que contiene una cabra en su selección inicial”. \(G\)=“El jugador gana el coche”.

Para calcular \(P(G)\), basta con notar que \(G=(G \cap A) \cup (G \cap B),\) ya que \(A \cap B = \varnothing\) y \(A \cap B = \Omega\) (esto es equivalente a decir que \({A,B}\) es una partición de \(\Omega\)) \[P(G)=P((G \cap A) \cup (G \cap B))=\] \[=P(G \cap A) + P( G \cap B))= P(G\mid A)\cdot P(A) + P(G\mid B)\cdot P(B)\] Tenemos que \(P(A) = 1/3\) y \(P(B) = 2/3\) pues hay un coche y dos cabras. Ahora calculamos la probabilidad de ganar el coche, \(P(G)\), en función de que el jugador acepte o no la oportunidad de cambiar de puerta elegida.

Jugador que no se cambia.

En este caso \(P(G\mid A) = 1\) y \(P(G\mid B) = 0\) pues el jugador se queda con su selección inicial, es decir \(P(G)=1/3\).

\[ P(ganar)=P(coche\mid (eligiendo \ bien\ al \ principio))\cdot P(elegir \ bien\ al\ principio)+\] \[+P(coche\mid (elegir \ mal\ al\ principio))\cdot P(elegir \ mal\ al\ principio) =1\cdot \frac{1}{3}+0\cdot \frac{2}{3}=\frac{1}{3}\]

Jugador que cambia.

En este caso \(P(G\mid A) = 0\) y \(P(G\mid B) = 1\) pues el jugador se cambia a la única puerta cerrada que queda (y sabemos que como el presentador sabe dónde está el coche, siempre mostrará una cabra).

\[ P(ganar)=P(coche\mid (eligiendo \ bien\ al \ principio))\cdot P(elegir \ bien\ al\ principio)+ \] \[+P(coche\mid (elegir \ mal\ al\ principio))\cdot P(elegir \ mal\ al\ principio) =1\cdot \frac{1}{3}+0\cdot \frac{2}{3}=\frac{1}{3} \]

Claramente la mejor estrategia es cambiar siempre, pues la probabilidad efectiva de ganar es el doble de la correspondiente al jugador que no cambia nunca.

El físico y youtuber Javier Santaolalla habla de este problema y de la historia que rodea el mismo (muy interesante).

4.21.2 Paradoja de los hijos

El matrimonio Smith camina por la calle y se encuentra a don Pepito. Don Pepito reconoce a su amigo del colegio José Smith, así que se detienen a saludarse: “Hola, don Pepito”, “Hola, don José”. “¿Recuerda usted a mi esposa?”-dice don José, señalando a su pareja. Don Pepito asiente-. ¿Y a mi hijo Joseíto? -dice, señalando a un chico que va a su lado.

Sabiendo que el matrimonio Smith tiene dos hijos, ¿cuál es la probabilidad de que el otro hijo sea también varón? (Suponemos que la probabilidad de nacer hombre o mujer es 0.5).

A primera vista, da la impresión de que la probabilidad es 0.5. Lo que ocurre es que, aunque no lo parezca, tenemos una información que modifica esa probabilidad. Si un matrimonio tiene dos hijos, el espacio muestral de los posibles resultados (en cuanto al sexo) de los hijos es \[\Omega=\{H_1 H_2,H_1 M_2,M_1 H_2,M_1 M_2\},\]

donde estamos utilizando la notación \(H_1 H_2\) indicando: hijo menor hombre, hijo mayor hombre… Pero, ya que sabemos que uno de los hijos es hombre (el que acompaña a sus padres), tenemos que el suceso \(M_1 M_2\) no puede darse, luego el espacio muestral se reduce a \[\Omega =\{H_1 H_2,H_1 M_2,M_1 H_2 \}\] con lo que vemos que la probabilidad de que el otro hijo sea hombre es la probabilidad de que los dos hijos sean hombres (\(H_1 H_2\)) que es 1/3.

Resolver el problema anterior (calcular la probabilidad de que el otro hijo del matrimonio sea varón), sabiendo que el hijo que está paseando con el matrimonio nació un martes (suponemos que todos los días son equiprobables para nacer).

Ahora sí que parece imposible que pueda servir de algo que nos digan que el hijo (Joseíto) que pasea con el matrimonio nació en martes. Pues en realidad sí que es una información que condiciona la probabilidad que queremos obtener. Llamemos \(H\)=”hombre”, \(M\)=”mujer”, \(A\)=”un hijo varón nació en martes”, y utilizaremos subínidices 1 y 2 para indicar hija(o) menor o hija(o) mayor. La probabilidad que nos piden es \[P (H_1H_2\mid A)=\frac{P(H_1 H_2 \cap A)}{P(A)}\]

En el numerador tenemos que calcular la probabilidad de que, teniendo dos hijos, los dos sean varones y uno nazca en martes. Puede ocurrir:

• El primero nace en martes y el segundo no.

• El primero y el segundo nacen en martes.

• El primero no nace en martes y el segundo tampoco.

Los casos posibles son Lunes y Lunes, Lunes y Martes,…, Martes y Lunes,…; hasta Domingo y Domingo. Total \(49\) casos. Los casos favorables son Martes y Lunes, Martes y Martes,… Martes y Domingo (7) y luego Lunes y Martes, Lunes y Miércoles, …, Lunes y Domingo (6: Martes y Martes no podemos considerarlo dos veces). Por lo tanto, el numerador es \(13/49\).

Vamos con el denominador. Los casos posibles son \(49\), igual que antes. Los casos favorables son los días a considerar según las posibilidades \(H_1 H_2, M_1 H_2, H_1 M_2\) (primer hijo hombre y segundo hombre, primer hijo hombre y segundo mujer…. ).

• En el primer caso, las posibilidades pueden ser \(13\) (es lo ocurrido con el numerador).

• En el segundo caso serían Martes y Lunes, Martes y Martes, …, Martes y Domingo. Total \(7\).

• El el tercer caso serían Lunes y Martes, Martes y Martes, …, Domingo y Martes. Total \(7\).

Por consiguiente, el denominador es \(13+7+7= 27\) dividido entre \(49\). Finalmente, la probabilidad es \((13/49)/(27/49)=13/27\)

4.21.3 Problema del prisionero (Hardin, 1968).

En una cárcel, tres prisioneros de historiales similares, solicitan el indulto a un tribunal. Poco después se sabe que el indulto ha sido concedido a dos de los tres presos. Uno de los prisioneros conoce a uno de los miembros del tribunal y sabe que si le pregunta podrá obtener algo de información. Podrá preguntarle por el nombre de uno de los indultados, pero no podrá preguntar si él es uno de ellos.

Reflexionando, concluye que, si no pregunta, la probabilidad de ser uno de los indultados es \(2/3\); mientras que, si pregunta, obtendrá una respuesta, y entonces la probabilidad de ser él otro de los indultados es \(1/2\). Por lo tanto, concluye que será mejor no preguntar, puesto que eso solo le servirá para disminuir su probabilidad de ser uno de los indultados.

¿Es correcto el razonamiento del preso?

En este caso, el conocimiento de la ocurrencia de un suceso (nombre de un indultado) no condiciona la probabilidad de que el preso que pregunta sea o no indultado, puesto que eso ya ha sucedido, y no hay ninguna acción (cambio de puerta) que vaya a modificar la probabilidad. La probabilidad es la misma a priori que a posteriori.

• Consideremos ahora el siguiente enunciado: Tres prisioneros esperan encarcelados su juicio sabiendo que sólo uno de ellos morirá. El juez le dice al primer preso que el tercero se salva y le pregunta si quiere intercambiar su suerte con el segundo. ¿Qué debe hacer el primer prisionero?

Como vamos a ver, este problema es equivalente al problema de Monty Hall. Llamamos \(S\)=”salvarse”, \(A\)=”tener suerte al principio”, \(B\)=”tener mala suerte al principio” \[P(S)=P(S\mid A)\cdot P(A)+P(S\mid B)\cdot P(B)\]

Prisionero que no se cambia.

En este caso \(P(S\mid A) = 1\) y \(P(S\mid B) = 0\) pues el prisionero no quiere cambiar.

Por lo tanto \(P(S) = 1/3\). En efecto: \[P(S)=P(salvarse\mid (teniendo \ suerte \ al \ principio))\cdot P(tener\ suerte \ al \ principio)+ \] \[ +P(salvarse\mid (teniendo \ mala \ suerte \ al \ principio))\cdot P(tener \ m.s.a.p.)= \]
\[=1\cdot \frac{1}{3}+0\cdot \frac{2}{3}=\frac{1}{3} \]

Prisionero que cambia

En este caso \(P(S\mid A) = 0\) y \(P(S\mid B) = 1\) pues el prisionero se cambia. Por lo tanto \(P(S) = 2/3\). En efecto: \[ P(S)=P(salvarse\mid (teniendo \ suerte \ al \ principio))\cdot P(tener\ suerte \ al \ principio)+ \] \[ +P(salvarse\mid (teniendo \ mala \ suerte \ al \ principio))\cdot P(tener\ m.s.a.p.)= \] \[ =0\cdot \frac{2}{3}+1\cdot \frac{2}{3}=\frac{2}{3}. \]

4.21.4 Paradoja de la caja de Bertrand, o Gold-Silver box (Bertrand, 1988).

Tenemos tres cajas, y cada caja tiene dos cajones, con una moneda cada uno: Una caja contiene dos monedas de oro, otra caja dos monedas de plata, y la caja final una de cada tipo. Después de elegir una caja al azar se toma un cajón al azar, y resulta que contiene una moneda de oro. ¿Cuál es la probabilidad de que la otra también sea de oro?

Muchos seguirán el siguiente razonamiento: Después de elegir una caja al azar y retirar una moneda también al azar, si esta resultase ser una moneda de oro, sólo tenemos dos opciones: (a) que hayamos elegido la caja con dos monedas de oro; o (b) que hayamos elegido la caja con una moneda de oro y otra de plata. Por tanto, la probabilidad de que la otra moneda también sea de oro es igual a \(1/2\). Esta solución es incorrecta. Veamos: Llamemos \(O_i\)=”moneda de oro en la extracción \(i\)”. Nos referimos al suceso obtener una moneda de oro la primera vez, y la segunda vez. Nos piden \(P(O_2\mid O_1)\)

Por Bayes: \[P(O_2\mid O_1)=\frac{P(O_1\mid O_2) \cdot P(O_2)}{P(O_1)}\]

La probabilidad de sacar una moneda de oro en la primera extracción depende de que cajón se haya seleccionado, es decir \[P(O_1 )=P(O_1\mid C_1)\cdot P(C_1 )+P(O_1\mid C_2)\cdot P(C_2 )+ P(O_1\mid C_3)\cdot P(C_3)\]

Cajón 1: dos oros. Cajón 2: oro y plata. Cajón 3: plata y plata. Luego \[P(O_1 )=1\cdot \frac{1}{3}+\frac{1}{2}\cdot \frac{1}{3}+0\cdot \frac{1}{3}=\frac{1}{2}\]

Ahora tenemos que darnos cuenta de que, cuando escribimos \(P(O_1\mid O_2)\) queremos calcular la probabilidad de que el primero fuera oro, sabiendo que el segundo lo fue, es decir \[P(O_1\mid O_2)=P(O_1\mid C_1)\]

ya que la única forma de que hayamos obtenido oro en la segunda extracción es que el primer oro fuese extraído en la caja 1, que es la que tiene dos oros.

En definitiva: \[P(O_2\mid O_1)=\frac{P(O_1\mid O_2)\cdot P(O_2)}{P(O_1 )} =\frac{P(O_1\mid C_1)\cdot P(C_1)}{P(O_1 )} =\frac{1\cdot \frac{1}{3}}{ \frac{1}{3}\cdot \frac{3}{2}}=\frac{2}{3}\]