8.5 Contrastes paramétricos y no paramétricos
Los contrastes pueden ser de tipo paramétrico o no paramétrico, según se refieran o no a parámetros de una población (a la media, a la varianza, a una proporción…).
Una hipótesis paramétrica es una afirmación sobre una o más características (parámetros) de una población. Si dicha hipótesis especifica un único valor para el parámetro la llamaremos hipótesis simple.
Si se especifica más de un valor para el parámetro la llamaremos hipótesis compuesta.
En un supermercado venden dos clases de naranjas, A y B. Las naranjas difieren en el diámetro, siendo en ambos casos de medias \(25\) y \(30\) cm, respectivamente. El diámetro sigue una distribución normal que, en ambos casos, tiene una desviación típica de \(2\) cm. Al llegar a casa, un señor ve que no le han puesto etiqueta a las bolsas, por lo que, en principio, no sabe cuál es cual. Teniendo en cuenta que las naranjas de la clase A son para él y las de la clase B para el vecino, necesita poder diferenciarlas.
Después de pensar un rato, el señor decide realizar el siguiente proceso para clasificar las naranjas: coge las de una bolsa (que son \(20\)), y las mide. Aceptará que son del tipo normal si la media de las longitudes no supera los \(28\) cm.
Vamos a calcular las probabilidades de los errores que es posible cometer.Se plantea el contraste \(H_{0}:\mu =30\) frente a \(H_{1}:\mu =25\). La regla de decisión es aceptar \(H_{0}\) si \(\bar{x}>28.\)
Recordemos que la variable normal es reproductiva, es decir, la suma de variables aleatorias normales sigue también una distribución normal:
si \(X_{\mathrm{1}},X_{\mathrm{2}},...,X_n\) son variables normales de media o esperanza \({\mu }_i\mathrm{=}E\mathrm{(}X_i\mathrm{)}\) y varianza \({\sigma }^{\mathrm{2}}_i\mathrm{=}Var\mathrm{(}X_i\mathrm{),} i\mathrm{=1,...,}n,\) la variable suma \(Y\mathrm{=}X_{\mathrm{1}}\mathrm{+}X_{\mathrm{2}}\mathrm{+...+}X_n\) es también una variable normal, de media la suma de las medias, y varianza la suma de varianzas (desviación típica = raiz de la suma de varianzas), es decir \[Y\mathrm{=}X_{\mathrm{1}}\mathrm{+}X_{\mathrm{2}}\mathrm{+...+}X_n\ \in \ N\left(\sum^n_{i\mathrm{=1}}{}{\mu }_i,\sqrt{\sum^n_{i\mathrm{=1}}{}{\sigma }^{\mathrm{2}}_i}\right).\]
\(X\in N(\mu ,\sigma )\) entonces, dada una muestra de tamaño \(n,\) la media muestral \(\bar{x}\in N(\mu ,\frac{\sigma }{\sqrt{n}}).\)
\(P(\)Error tipo I\()=P(\)Rechazar \(H_{0}\ \)siendo cierta\()=P(\bar{x}\leq 28/H_{0}\) es cierta).
\(P(\)Error tipo II\()=P(\)Aceptar \(H_{0}\ \)siendo falsa\()=P(\bar{x}>28/H_{0}\) es falsa).
Si \(H_{0}\) es cierta, \(\mu =30,\) luego \(\bar{x}\in \left(30,\dfrac{2}{\sqrt{20}}\right).\)
\[\begin{equation*} P(\bar{x}\leq 28/H_{0}\text{ es cierta})=P(\bar{x}\leq 28/\mu =30)= \end{equation*}\] \[\begin{equation*} =P\left( Z\leq \frac{28-30}{\frac{2}{\sqrt{20}}}\right) =P\left( Z\leq -4.472\right) \cong 0. \end{equation*}\]Si \(H_{0}\) es falsa\(,\mu =25,\) por lo tanto \(\bar{x}\in N\left(25,\frac{2}{\sqrt{20}}\right).\)
\[\begin{equation*} P(\bar{x}>28/H_{0}\text{ es falsa})=P(\bar{x}>28/\mu =25)= \end{equation*}\] \[\begin{equation*} =P\left( Z>\frac{28-25}{\frac{2}{\sqrt{20}}}\right) =P(Z>6.7)\cong 0 \end{equation*}\]Comprobamos que las probabilidades de cometer los errores de tipo I y II son prácticamente cero, por lo que el señor ha inventado una regla de decisión estupenda.
Ejemplos de hipótesis no paramétricas:
Como dijimos antes, la manera habitual de realizar un contraste o test de hipótesis es tomar una muestra, y ver si los resultados son coherentes o no con lo que se afirma en la hipótesis nula.
Supongamos que un investigador desarrolla un método o tratamiento para reducir el dolor. Para comprobar que el método es efectivo, habrá que observar una muestra de pacientes con dolor y, tras aplicarles el tratamiento, ver si el dolor ha disminuido.
Si la muestra consta, en general, de \(n\) pacientes, se observa en ellos la variable
\(X\)= dolor antes del tratamiento
Tendremos \(n\) datos \(x_1,x_2,...,x_n\).
Una vez realizado el tratamiento, volvemos a observar la variable
\(Y\)= dolor tras el tratamiento
Tendremos otros \(n\) datos \(y_1,y_2,...,y_n\). A continuación, restamos el dolor antes y el dolor después \(Z=X-Y\) y tenemos los datos \(z_1,z_2,..,z_n\) donde \(z_i=x_i-y_i\).
De manera general, si el tratamiento es efectivo, los valores de \(X\) serán mayores que los de \(Y\) (el dolor antes era más alto que el dolor después). Pero, en general, el descenso de dolor no va a ser igual en todos los pacientes. En unos se reducirá más, en otros menos. Por ello lo que interesa comprobar es si la reducción de dolor, en media, es grande o no lo es (porque si la reducción de dolor es pequeña, o casi nula, el tratamiento a lo mejor ni interesa por ser caro).
La hipótesis nula a comprobar, entonces, será de la forma:
\(H_0: \mu =0\)
donde \(\mu\) representa el nivel medio de disminución del dolor. Esta es la hipótesis que planteamos, porque es la que se pretende “falsar”, es decir, encontrar alguna prueba de que no es cierta (cuando usamos el tratamiento). Por lo tanto, lo interesante será (para demostrar que el tratamiento es efectivo) que la media de la muestra \((z_1,z_2,...,z_n)\) no sea un número próximo a cero.
Una posible forma de realizar un contraste sería por medio de un histograma. Fijémonos en la Figura siguiente. Tenemos \(3\) muestras o \(3\) grupos de notas de \(250\) alumnos. Claramente, el primero de los histogramas nos diría que la variable \(X\) es normal, puesto que su forma se parece a la campana de Gauss. Mientras, el segundo histograma nos diría que existe una asimetría a la derecha, y con el tercer histograma claramente rechazariamos la hipótesis nula.
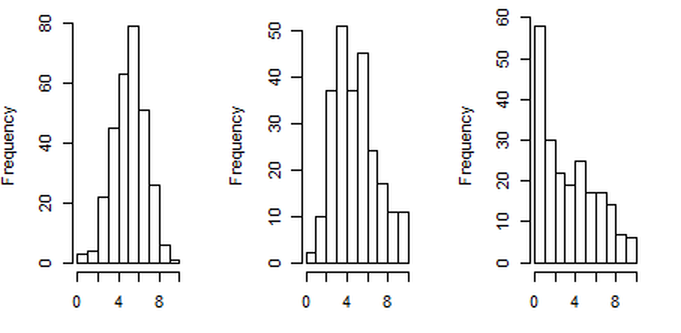
Figura 8.5: Tres posibles histogramas para una distribución de notas.
Este ejemplo sería un contraste de tipo no paramétrico, puesto que no se realiza ninguna afirmación sobre parámetros de la variable. Intentamos saber si \(X\) es una variable normal o no.
Desde un punto de vista estadístico, ¿cómo se debería proceder para saber si Kamal está haciendo trampa?.
Veamos: Si los dados están cargados en el 6, la probabilidad de salir un seis doble será mayor de lo que le correspondería, es decir: \(p \left( 6 \cap 6\right) =p_{0}=1/36.\)
Como en principio, todo malo, por muy malo que sea, tiene derecho a la presunción de inocencia, la hipótesis nula es cierto salvo que los resultados demuestren lo contrario. Vamos a plantear entonces las hipótesis nula y alternativa como
\(H_{0}:\) Los dados no están cargados, es decir
\(H_{0}: p=p_{0}=1/36\) frente a
\(H_{1}:\) Los dados sí estan trucados \((p>1/36)\).
Lo procedente, desde el punto de vista estadístico, es observar una serie larga de tiradas del dado por parte de Kamal, para ver si tiene más suerte de la que le correspondería por azar. Como hemos visto en el capítulo anterior, un estimador natural del parámetro \(p\) es la proporción muestral \(\hat{p}\)
Vamos a suponer que James Bond observa 30 tiradas de los dos dados, y que en esas 30 tiradas el seis doble sale 3 veces. Tenemos entonces una muestra en la cual En esta muestra, \(\hat{p}=3/30=0.1\) que es distinta y más grande que \(p_{0}=1/36=0.027.\)
Como vemos, existe una discrepancia. Ahora bien, ¿es porque realmente los dados están trucados, o el resultado es fruto de la casualidad en la muestra elegida? Dicho de otra manera: ¿qué probabilidad existe de que el dado no esté preparado (\(H_{0}\) es cierta) y que la muestra arroje una proporción muestral de \(0.1\). Dicho de otro modo: ¿Qué probabilidad existe de que el dado no este trucado (\(H_{0}\) es cierta) y que exista esa diferencia entre lo observado \((0.1)\) y lo teórico \((0.027)\)?
Veamos como lo solucionó James Bond:
La discrepancia obtenida entre lo que dice la hipótesis nula (\(p=0.027\)) discrepa de lo observado en la realidad (\(p=0.1\)). ¿Esta discrepancia es grande o pequeña? A simple vista parece grande, pero ¿podemos medirla de alguna forma?
En la terminología de Fisher:
\(T\)= medida de la discrepancia
\(T(x_1,x_2,...,x_n)\)=0.1-0.027
y tenemos que calcular el \(p-\)valor \(P(T\geq (x_1,x_2,...,x_n)/H_0),\)
El \(p-\)valor es la probabilidad de que los datos (si la hipótesis nula es cierta) se hayan obtenido por casualidad.
La forma “general” de medir la discrepancia entre un valor teórico y uno estimado es mediante la diferencia de ambos, dividida por la desviación típica.
Se utiliza la misma idea para medir la diferencia entre dos grupos, o dos tratamientos. Se comparan las medias dividiendo por la desviación típica.En este caso, El \(p\)-valor (más adelante vemos como se calcula) es 0.0073, por lo tanto, muy pequeño. Resulta así, muy difícil creer en que los datos no estén trucados.

Figura 8.6: Imagen del cómic Rue del Pércebe, 13, F. Ibáñez.