7.2 Estimación puntual

El objetivo de la estimación puntual es aproximar el valor del parámetro desconocido (tiempo medio de ejecución de un algoritmo, altura media de las mujeres de una población, diferencia del resultado medio entre dos tratamientos médicos, proporción de gente que mejora con un tratamiento médico…)

Para ello se utiliza la información de la muestra \((x_1,x_2,\ldots,x_n)\), a través de un estimador.

Algunos estimadores frecuentes son:

Media muestral, para estimar la media teórica de una variable \(X\).

\(\bar{x}=\dfrac{x_{1}+\cdots +x_{n}}{n}\)

Proporción muestral, para estimar una proporción \(p\):

\(\widehat{p}=\dfrac{x_{1}+\cdots +x_{n}}{n},\) siendo \(x_1, \ldots, x_n\) una muestra aleatoria simple de la variable \(X\in B(1,p)\), es decir, son unos o ceros.

Varianza muestral: para estimar la varianza teórica de una población, se puede usar la varianza de una muestra:

\(S^{2}=\dfrac{\left( x_{1}-\bar{x}\right)^{2}+\cdots +( x_{n}-\bar{x}) ^{2}}{n},\)

y también la llamada

Cuasi-varianza muestral:

\(S^{2}_{n-1}=\dfrac{( x_{1}-\bar{x}) ^{2}+\cdots +( x_{n}-\bar{x}) ^{2}}{n-1},\)

que corresponde a la varianza de la muestra, pero dividiendo por \(n-1\), en lugar de dividir por \(n\). En el capítulo de estadística descriptiva, ya comentamos que el R, por defecto, al calcular la desviación típica de una muestra, mediante el comando sd, calcula directamente la cuasi-varianza y luego obtiene la raiz cuadrada.

La evaluación del estimador sobre la muestra fija da lugar a una estimación puntual.

Cálculo de la media muestral tomando la muestra fija \((x_1,x_2,x_3)=(2,7,1)\). \[ \bar{x}=\dfrac{2+7+1}{3}=\dfrac{10}{3} \]

7.2.1 Propiedades de los estimadores

Estamos diciendo que un estimador es una aproximación de un parámetro teórico o desconocido de una población. Para estimar la media de la altura de una población, podemos seleccionar una muestra y calcular la media aritmética de la muestra. Ahora bien, también tendría sentido usar como estimador el siguiente: \[ \dfrac{min(x_1,x_2,\ldots,x_n) + max(x_1,x_2,\ldots,x_n)}{2} \] ¿Cuál de los dos se aproxima más al verdadero valor desconocido? En principio, no habría manera de saberlo, puesto que deberíamos conocer el valor teórico (el desconocido). Por eso, interesa estudiar propiedades de los estimadores, que nos permitan decidir entre usar unos u otros para los casos concretos.

7.2.1.1 Estimadores insesgados

Una primera propiedad deseable para un estimador es que el centro de la distribución de los valores que puede tomar coincida con el valor del parámetro que queremos aproximar.

A esta propiedad se le llama insesgadez. Así, un estimador insesgado es aquel cuya media coincide con el valor del parámetro a estimar.

Veámoslo con un ejemplo para entenderlo mejor: supongamos que deseamos tener una estimación de la estatura media de los hombres mayores de 18 en una población. Podriamos ponernos en medio de la calle y seleccionar aleatoriamente una muestra de \(n\) hombres, medir su estatura (o preguntársela) y calcular después la media aritmética de los datos obtenidos. Esa sería una estimación puntual; llamémosla \(\bar{x}_1\).

Figura 7.2: Encuestador y encuestada.

Por medio de R podemos hacer una simulación de este proceso. En vez de bajar a la calle, parar a la gente y preguntarle lo que mide, simulamos cien datos correspondientes a \(100\) estaturas de varones mayores de \(18\). En este caso, tenemos que “simular” que medimos a cien personas, de una población de varones españoles mayores de \(18\).

# Consideremos n =100 personas 
set.seed(1)
n=100 
# asi se simulan n datos que siguen
# una distribución normal de  
# media 177.7  y desviación típica 5.9 :
X1=rnorm(n,177.7,5.9) 
# dibujamos el histograma:
hist(X1, probability = TRUE, col = 'lightblue', 
main="100 estaturas de varones mayores de 18")
# dibujamos los puntos:
rug(X1)
# dibujamos la estimación de la densidad:
lines(density(X1), col="red",lwd=2)

Figura 7.3: Histograma y estimación de la densidad de 100 estaturas.

La media muestral de esos \(100\) valores es \(\bar{x}_1\)= 178.3424.

Si vamos al dia siguiente a la misma calle y seleccionamos aleatoriamente otra muestra del mismo número \(n\) de personas, medimos su estatura y calculamos la media aritmética, tenemos otra estimación puntual (\(\bar{x}_2\)).

# Otras 100 personas 
n=100
X2=rnorm(n,177.7,5.9)

La media es \(\bar{x}_2\)=177.4769.

Obviamente, estos valores \(\bar{x}_1\) y \(\bar{x}_2\) no coinciden, y no tienen por qué coincidir. En cada caso, hemos seleccionado \(100\) personas aleatoriamente, hemos medido su estatura y hemos calculado la media muestral. Los datos no van a ser los mismos, y por lo tanto las medias muestrales tampoco. Cada vez que seleccionemos otra muestra, el estimador media muestral da un valor diferente. Esto es, la media muestral es una variable aleatoria.

Vamos ahora a suponer que realizamos este proceso un número grande \(B\) de veces; es decir, salimos a la calle, medimos a \(100\) personas, y calculamos la media muestral; al día siguiente volvemos a hacer lo mismo, y así sucesivamente, haste \(B =250\) veces, por ejemplo. Mediante el siguiente procedimiento en R, simulamos este procedimiento y hacemos una gráfica (Figura 7.4) de la distribución de los \(250\) valores obtenidos.

n=100;B=250
s<-0
for (i in 1:B) s[i]=mean(rnorm(n,177.7,5.9))
hist(s, probability = TRUE, col = 'lightblue', 
main="250 datos de la media")
rug(s)
lines(density(s), col="red",lwd=2)

Figura 7.4: Histograma y estimación de la densidad de las 250 MEDIAS de todas las muestras.

La media de estos \(250\) valores es 177.7205 que es muy próxima al verdadero valor \(177.7\)

De esta forma, comprobamos que la media (de las diferentes medias) se aproxima al verdadero valor \(177.7\). Matemáticamente, se puede demostrar que siempre ocurre así; es decir, que la media muestral es un estimador insesgado.

Veamos otro ejemplo:

Figura 7.5: Seres extraños de otra galaxia.

Supongamos que preguntamos en la calle si la gente cree o no en los extraterrestres. En este caso, las respuestas van a ser “Sí” o “No”, que anotaremos como \(1\) o \(0\), es decir valores de una variable aleatoria de Bernoulli de parámetro \(p\), siendo \(p\)=proporción de gente que cree en los extraterrestres, que es el 61 por ciento (sacado de aqui). Hacemos como en el caso anterior: cogemos una muestra de tamaño 100 (o cualquier otro número un poco grandecito), preguntamos y anotamos la respuesta. Pero, en vez de hacerlo realmente, lo simulamos con el ordenador, de esta forma:

# Consideremos n =100 personas 
set.seed(1)
n=100
# así se simulan n datos que siguen
# una distribución de Bernoulli de parámetro 0.61
Y1=rbinom(n,1,0.61)  
pander(table(Y1))

0	1
42	58

El número de unos en esta encuesta (gente que dijo que creía en los extraterrestres) es de 58, con lo que la proporción muestral es \(\hat{p}_1=\) 0.58.

Si vamos al dia siguiente a la misma calle y seleccionamos aleatoriamente otra muestra del mismo número \(n\) de personas, les preguntamos lo mismo, tendremos otra estimación puntual del número de gente que cree en los extraterrestres (\(\hat{p}_2\)).

n=100
Y2=rbinom(n,1,0.61)   
pander(table(Y2))

0	1
38	62

El número de unos en esta encuesta (gente que dijo que creía en los extraterrestres) es de 62, con lo que la proporción muestral es \(\hat{p}_2=\) 0.62.

Vamos ahora a suponer que realizamos este proceso un número grande \(B\) de veces; es decir, salimos a la calle, le preguntamos a 100 personas, calculamos la proporción muestral; al día siguiente volvemos a hacer lo mismo, y así sucesivamente, haste \(B\)=250 veces, por ejemplo. Mediante el siguiente procedimiento en R, simulamos este procedimiento y hacemos una gráfica (Figura 7.6) de la distribución de los 250 valores obtenidos.

n=100;B=250
x<-0
for (i in 1:B) x[i]=sum(rbinom(n,1,0.61))/n
hist(x, probability = TRUE, 
col = 'lightblue', main="250 encuestas")
rug(x)
lines(density(x), col="red",lwd=2)

Figura 7.6: Histograma y estimación de la densidad de los valores obtenidos en cada una de las 250 muestras.

La media de estos 250 valores es 0.6119 que es muy próxima al verdadero valor \(0.61\)

Para que se pueda entender este ejemplo mejor, supongamos que las muestras seleccionadas son de tamaño 7, y realizamos el proceso 15 veces. A continuación realizamos una simulación donde podemos observar todos los detalles: para cada muestra, los valores \(1\) o \(0\) denotan si la persona en cuestión ha contestado “Sí” o “No”, y, a la derecha, calculamos la proporción muestral de “Síes”, es decir el número de ellos dividido por (en este caso) \(7\).

n=7
B=15
muestras <- as.data.frame(matrix(rbinom(n*B,
                         1, 0.61), ncol=n))
rownames(muestras) <- paste("muestra", 1:B, sep="")
muestras$mean <- rowMeans(muestras[,1:n])
ptilde<-muestras$mean
colnames(muestras) <- c(paste(" obs", 1:n , 
                        sep=""), " ptilde")
# muestras:
pander(muestras)

	obs1	obs2	obs3	obs4	obs5	obs6	obs7	ptilde
muestra1	0	1	1	0	0	0	0	0.2857
muestra2	0	1	1	1	0	1	1	0.7143
muestra3	0	1	1	1	0	0	1	0.5714
muestra4	0	1	0	0	1	0	1	0.4286
muestra5	1	1	1	0	0	1	0	0.5714
muestra6	0	1	0	1	1	0	0	0.4286
muestra7	0	0	1	1	1	1	0	0.5714
muestra8	1	0	1	1	1	0	1	0.7143
muestra9	1	0	1	0	1	0	1	0.5714
muestra10	1	1	1	1	1	1	0	0.8571
muestra11	0	1	1	1	1	1	1	0.8571
muestra12	1	1	0	0	1	0	1	0.5714
muestra13	1	0	0	0	1	0	1	0.4286
muestra14	1	1	1	1	1	0	1	0.8571
muestra15	1	0	0	1	1	1	1	0.7143

mean(ptilde)

## [1] 0.6095

Observamos que la proporción muestral también es un estimador insesgado.

7.2.1.2 Estimadores consistentes

Un estimador insesgado es consistente cuando su varianza tiende a 0 si \(n\) crece hacia infinito.

Recordemos que la varianza mide la dispersión. A mayor varianza, mayor dispersión entre los valores de la variable, y a menor varianza menor dispersión. La propiedad de consistencia indica que, si tomamos muestras muy grandes (\(n\) muy grande, creciendo hacia infinito), la varianza se hará próxima a cero, es decir que obtendremos siempre valores muy próximos entre sí.

Pensemos en los ejemplos que hemos estado viendo donde realizabamos encuestas en la calle (o medíamos la estatura). Lo hacíamos en muestras de tamaño 100, y obteníamos valores diferentes para nuestro estimador (o bien la media muestral, o bien la proporción muestral). Parece lógico pensar que, si en vez de tomar muestras de tamaño 100, tomamos muestras muy grandes, los valores que obtengamos de cada vez se parezcan mucho entre si (por lo tanto la dispersión o varianza tiende a cero), puesto que es como si estuviésemos de cada vez midiendo a (casi) toda la población.

7.2.2 Propiedades de la media muestral

La media muestral \(\bar{X}=\dfrac{X_{1}+\cdots +X_{n}}{n}\):

Es un estimador de la media poblacional \(\mu\).
Es insesgado.
Es consistente.
Si \(X\in N(\mu ,\sigma )\) entonces \(\bar{X}\in N(\mu ,\sigma\sqrt{n}).\)

7.2.3 El error estándar de la media (muestral).

Esta última propiedad nos dice que, si consideramos muestras de una variable normal (como la estatura), la media muestral (la media de las muestras, que es otra variable aleatoria, como hemos visto), sigue también una distribución normal (recordemos que, en el ejemplo de arriba, donde simulamos 250 muestras de cien estaturas, el histograma de las medias muestrales tenía la forma de la campana de Gauss).

Si \(X\) no sigue una distribución normal, pero tiene una media \(\mu\) y una desviación típica \(\sigma\) finitas, entonces, por el teorema central del límite \(\bar{X}\approx N(\mu ,\sigma\sqrt{n}).\)

Esta propiedad es casi como la inmediatamente anterior. Si las variables que consideremos no siguen una distribución normal, pues no hay excesivo problema, puesto que, por el teorema central del límite, la media muestral seguirá aproximadamente una distribución normal (siempre que se promedien bastantes variables; en la práctica, más de \(30\)).

El resultado nos dice que \(\bar{X}\in N(\mu ,\sigma\sqrt{n})\) (exacta o aproximadamente, según acabamos de comentar), es decir que el parámetro media de la variable \(\bar{X}\) es, precisamente, la media teórica (la misma de la variable \(X\)), y la desviación típica es la misma que la teórica, pero dividida por \(\sqrt{n}\). Esto se conoce como el error estándar de la media muestral. Por ejemplo, en muestras de tamaño 100, la desviación típica o error estándar es la de la variable \(X\) dividida por 10. En muestras de tamaño 10000, \(\sigma\) aparece dividida solo por 100. Esto nos mide, en cierta manera, la “velocidad” en que la dispersión se va acercando a cero. Y vemos que con tamaños de muestra, por ejemplo, de un millón (que ya es una señora muestra), la desviación típica solo aparece dividida por mil.

En el capítulo \(10\) del libro “Pensar rápido, pensar despacio” (D. Kahneman 2014) Daniel Kahneman explica que la mente humana tiende automáticamente a sacar conclusiones y explicaciones causales de resultados que, procedentes de muestras pequeñas y poco representativas, son meras ilusiones estadísticas, carentes de significado. Kahneman llama a ese frecuente error la “ley de los pequeños números”.

Ilustra el fenómeno con los resultados de un estudio sobre la distribución geográfica del porcentaje de cáncer de riñón entre los más de 3.000 condados de Estados Unidos. Se observó que los porcentajes más bajos se daban en condados rurales poco poblados del Oeste, Medio Oeste y Sur de los Estados Unidos, de esos (añade Kahneman irónicamente) donde predominan los votantes del Partido Republicano.

Como no parece lógico que la intención de voto proteja contra el cáncer, surgen otras explicaciones mucho más sensatas: la vida rural es más sana, con menos estrés, mejor alimentación, menos contaminación, etc.

Sin embargo, al observar, en el mismo estudio, los lugares con mayor incidencia del cáncer de riñón, la localización geográfica era la misma. Si no se ha leído el párrafo anterior, uno podría plantearse que en el medio rural hay peor alimentación (rica en solo ciertos contenidos y pobre en otros), peor acceso a la sanidad, etc.

El gráfico 7.7 muestra los resultados citados: en naranja, los condados con porcentajes más altos de cáncer de riñón; y, en verde, aquellos con porcentajes más bajos. En general, unos están pegados a los otros.

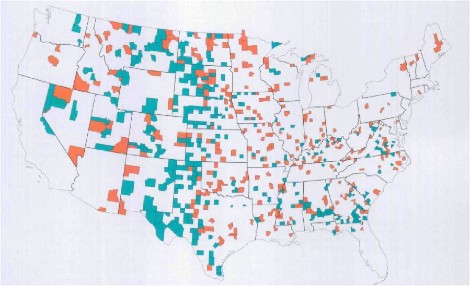
Figura 7.7: Tasas de cáncer de riñon en USA.

La explicación la ofreció el estadístico americano Howard Wainer en el artículo “The most dangerous equation” (Wainer 2007) (de donde procede el gráfico): las llamativas diferencias en la incidencia del cáncer entre condados obedecen al azar.

En efecto, si en Estados Unidos se dan, en promedio, \(5\) casos de cáncer de riñón por cada \(100.000\) habitantes, la “ley de los grandes números” hará que la incidencia de la enfermedad esté muy próxima a ese valor en los condados muy poblados (como en Los Angeles). Pero, en los que tengan poca población, ese promedio oscilará mucho, pues la variabilidad (desviación estándar) de la media aritmética de la variable analizada -en nuestro caso, el número de casos de cáncer de riñón por habitante- guarda una relación inversa con el tamaño de la muestra usada para calcularla (o, para ser exactos, de su raíz cuadrada).

Por eso, según Wainer, la gran diferencia estadística entre condados en la incidencia de la enfermedad no es un “hecho” (fact) genuino , sino un “artefacto” (arti-fact), es decir un resultado artificial nacido de la interacción entre el azar y el tamaño de las “muestras” utilizadas para calcular la incidencia media.

Así, cuando el tamaño de las muestras (\(n\)) es muy grande -como ocurre en condados con mucha población-, la variabilidad de los valores medios que salgan será muy pequeña: tales valores medios nos saldrán muy parecidos al valor medio de la variable en el conjunto de la población (en nuestro ejemplo, el \(5\) por \(100.000\) habitantes con cáncer de riñón que se da en Estados Unidos, considerado como un todo).

Wainer explica que la gran variabilidad de los valores medios en muestras pequeñas se da también en las notas medias de los alumnos de una escuela o clase: cuanto más pequeña sea la escuela o clase, más frecuente será que la nota media de sus alumnos tome valores extremos, altos o bajos. Así, que muchas de las mejores notas medias se alcancen en escuelas pequeñas no obedecerá necesariamente a que sean mejores, sino al puro azar.

Wainer señala que la Fundación Gates ignoró esa relación cuando en los años 90 dedicó muchos millones de dólares a fomentar las escuelas pequeñas, a la vista de que un elevado porcentaje de las escuelas con mejores resultados académicos tenían pocos alumnos. Pero abandonaron la idea cuando advirtieron que ese fenómeno estadístico podía obedecer al azar: también las escuelas pequeñas estaban sobre-representadas entre las que obtenían los peores resultados. O sea, las escuelas pequeñas, en efecto, contaban con los mejores alumnos, pero también contaban con los peores.

Esta argumentación sirve para responder al siguiente problema, planteado en naukas por Pablo Rodríguez en 2014:

“Un acertijo: bebés y probabilidad.
En una ciudad hay dos hospitales. Uno de ellos es mucho más grande que el otro, y por lo tanto tiene capacidad para más pacientes. El mes pasado sucedió una cosa curiosa. La sala de maternidad de uno de los hospitales registró que la proporción de bebés niña había sido ese mes muy superior a la de bebés niño (pongamos \(75\%\) de niñas, \(25\%\) de niños). ¿En cuál de los dos hospitales es más probable que sucediese esta rareza, en el hospital grande o en el hospital pequeño?
Para los más exigentes en cuánto a detalles, dejo las siguientes aclaraciones: Consideramos que las probabilidades en cada parto son \(50\%\) niño \(50\%\) niña. No tiene importancia sobre el resultado final, pero pongamos que ese mes no hubo partos múltiples de gemelos o mellizos. La única diferencia relevante entre el hospital grande y el pequeño es que el hospital grande atendió a muchas más madres que el pequeño.

En el propio blog de Pablo Rodríguez da tres explicaciones, que resumo (ir al original para ampliar las ideas):

Explicación intuitiva:

En donde la muestra es más pequeña (hospital pequeño), es más fácil que una rareza (en el sentido probabilístico, algo de poca probabilidad) destaque; puesto que, en donde la muestra es más grande (hospital grande), las frecuencias van a compensarse. De hecho, la ley de los grandes números nos recuerda que la frecuencia relativa de ocurrencia de un suceso tenderá a su probabilidad cuando el número de repeticiones sea grande.

Explicación con teoría:

El nacimiento de un bebé se puede modelar como una variable de Bernoulli: dos posibles sucesos, complementarios uno del otro. Los distintos nacimientos en un hospital van a constituir, por lo tanto, una variable Binomial. Llamemos, por ejemplo, \(X\)=número de niñas nacidas en un hospital, tras n partos. Esta variable es una variable Binomial de parámetros \(n\) y \(p=0.5\).

Podemos calcular la probabilidad de que el número de niñas nacidas sea mayor que el \(75\%\) del total como \(P(X>0.75\cdot n)\). Cambiando el valor de \(n\) podemos ir viendo los resultados. En R, la probabilidad \(P(X\leq c)\) en una binomial \(Bi(n,p)\) se calcula con pbinom(c,n,p); por lo tanto, \(P(X>0.75\cdot n)\) será \(1- P(X\leq 0.75\cdot n)\).

Para \(n=10,\)

n=10
c=0.75*n
p=0.5
1-pbinom(c,n,p)

## [1] 0.05469

Vemos que, para \(10\) camas, solo ocurriría esto en un \(5.46\%\) de los casos.

Para \(n=30,\)

n=30
c=0.75*n
p=0.5
1-pbinom(c,n,p)

## [1] 0.002611

esto solo ocurriría en un \(0.26\%\) de los casos.

Estas (y algunas otras) curiosidades estadísticas también han sido analizadas por Manuel Conthe (licenciado en Derecho, Economista del Estado y ex-presidente de la Comisión Nacional del Mercado de Valores, entre otros méritos) en expansion. Son destacables también los siguientes párrafos:

“Pero creo que también acertó el presidente Rajoy cuando en un acto público en Nueva York manifestó: Permítanme que haga un reconocimiento a la mayoría de españoles que no se manifiestan, que no salen en las portadas de la prensa y que no abren los telediarios. No se les ve, pero están ahí”.

“La prensa es como el rayo de una linterna que se mueve sin cesar y saca de la oscuridad un suceso tras otro. Las noticias y la verdad no son lo mismo, y deben distinguirse”.

“Nuestra mente, por desgracia, no sólo tiende a identificarlas, sino que, como enseña Kahneman, tiende a deducir verdaderas generales de artefactos nacidos del azar. Por eso, cuando los medios eligen sus encuadres no iluminan: construyen su realidad.”

7.2.4 Propiedades de la cuasi-varianza (muestral)

A estas alturas ya no nos acordamos de lo que es. Refresquemos:

La cuasi-varianza muestral \(S^{2}_{n-1}=\dfrac{ ( X_{1}-\bar{X} ) ^{2}+\cdots + ( X_{n}-\bar{X}) ^{2}}{n-1}\):

Es un estimador de la varianza poblacional \(\sigma^2\).
Es insesgado (el motivo de dividir por \(n-1\) es que, de esta forma, el estimador cumple esta propiedad. Si se divide por \(n\), esta propiedad no se verifica.
Es consistente.
Además, \(S^{2}_{n-1}=\frac{n}{n-1}S^{2}\) (la relación entre la varianza muestral y la cuasi-varianza es muy simple).

7.2.5 Propiedades de la proporción muestral

La proporción muestral \(\widehat{p}=\dfrac{X_{1}+\cdots +X_{n}}{n}\):

Es un estimador de la proporción poblacional \(p\).
Es insesgado.
Es consistente.
Para \(n\) grande (\(n>30\)), por el Teorema Central del Límite, se tiene que \(\widehat{p}\approx N(p,\sqrt{p(1-p)/n})\)

En una clínica de fisioterapia desean saber el número medio de grados que puede doblar una rodilla destrozada, tras un tratamiento de diez sesiones de rehabilitación (el seguro no paga más) con un método nuevo recién salido al mercado. Se seleccionan diez pacientes y, tras dos semanas de tratamiento, se mide el número de grados que dobla la rodilla hasta que los gritos son inaguantables: \[41.60, 41.48, 42.34, 41.95, 41.86, 42.41, 41.72, 42.26, 41.81, 42.04.\]

Para estimar la media poblacional (parámetro desconocido en este caso) podemos considerar la media muestral:

\[\bar{x}=\dfrac{1}{n}{{\displaystyle\sum_{i=1}^{10}}x_i}=\dfrac{419.47}{10}=41.947\]

Si nos pidiesen estimar una proporción; por ejemplo, proporción de pacientes que doblarán más de 42 grados, (\(p=P(X>42)\)) podríamos utilizar la proporción muestral:

\[\hat{p}=\dfrac{1}{n}{{\displaystyle\sum_{i/ x_i >42}}1}=\dfrac{4}{10}=0.4\]

References

Kahneman, D. 2014. Pensar Rápido, Pensar Despacio / Thinking, Fast and Slow. Debolsillo Mexico.

Wainer, Howard. 2007. “The Most Dangerous Equation.” American Scientist 95 (3): 249.