5.3 Variables aleatorias continuas

Una variable aleatoria continua es aquella que puede tomar cualquier valor (al menos teóricamente) entre 2 fijados. Los valores de la variable (al menos teóricamente) no se repiten.

“Tiempo observado al recorrer una cierta distancia”, “estatura”, “peso”, “nivel de colesterol en sangre”…

Todas las precisiones realizadas en el capítulo de variables estadísticas son igual de adecuadas en este caso. Cuando observamos valores de una variable aleatoria continua, existe una limitación en cuanto al número de valores que puede tomar la misma. Esto es, en la práctica, la variable no toma infinitos valores. A la hora de medir el peso o la estatura, por ejemplo, se trabaja con un número preciso de decimales (que puede ser grande pero nunca será infinito). Lo que se está haciendo es lo que se llama una discretización a la hora de tomar datos. Sin embargo, desde un punto de vista matemático, consideraremos siempre que una variable continua puede tomar infinitos valores. Esto nos permitirá trabajar con propiedades matemáticas que nos aportarán mucha información de la variable considerada.

5.3.1 Función de densidad

Igual que una variable aleatoria discreta viene caracterizada por su función de probabilidad, las variables aleatorias continuas vienen caracterizadas por una función llamada función de densidad, que es una generalización de la función de probabilidad.

Matematícamente, una función \(f\) es una función de densidad si verifica dos propiedades:

\(f(x)\) es mayor o igual que cero en cualquier punto \(x\) (el dibujo de la función debe estar por encima del eje horizontal).
\(\int_{-\infty }^{\infty} f(x)dx =1\) (el área bajo la curva y el eje horizontal vale uno).

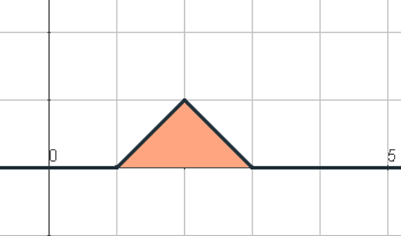
Figura 5.3: Ejemplo de una función de densidad bien simple.

El concepto de función de densidad procede de considerar que tenemos una población con todos sus (infinitos) datos o posibles valores y dibujamos el histograma, polígono de frecuencias o estimación de la densidad.

Supongamos que nos ponemos en medio de la calle y a cada mujer mayor de 18 años le preguntamos su estatura. Hacemos esto hasta tener una muestra de 15 datos y, a continuación, clasificamos los datos en intervalos, construimos el histograma y el polígono de frecuencias.

x=rnorm(15, 163,9)
print(x)

[1] 162.8 170.7 176.1 155.3 156.7 180.1 145.3 172.4 [9] 174.5 184.5 157.6 152.3 175.6 162.2 160.4

df<-data.frame(x)
N=length(x)
y=rep(0,N)
df2<-data.frame(x=x,y=y)
ggplot(df )+
  geom_histogram(aes(x=x), fill="lightblue")+
  geom_freqpoly(aes(x=x))+
  geom_point(data=df2, aes(x=x,y=y),
             size=1, col="magenta")

Ahora lo hacemos 50 veces

Ahora 200 veces

Ahora 1000 veces

Observamos como el polígono de frecuencias se va “perfilando” y suavizando, hasta construir el dibujo de una curva, a medida que tenemos más datos.

Obviamente, no estamos tomando datos en la calle, sino “simulándolos” en el ordenador. Mediante la función de R rnorm estamos generando números aleatoriamente, pero que corresponden a médidas reales de mujeres en España mayores de 18 (la media es, aproximadamente, 163 cm y la desviación típica 9). En el tema siguiente, en el que se habla de la distribución normal, se entenderá mejor todo esto. Ahora, lo único con que tenemos que quedarnos es que, paulatinamente, vamos añadiendo más datos de estaturas en nuestra muestra.

Con cada gráfica, el polígono de frecuencias acaba convirtiéndose en una curva que verifica las dos propiedades de la función de densidad (es una función no negativa y el área bajo la curva es uno, puesto que es el área bajo el polígono de frecuencias. Puede demostrarse geométricamente que el área bajo un polígono de frecuencias coincide con el ára existente bajo un histograma de frecuencias, y el área total del histograma corresponde al cien por cien de los datos).

La función de densidad corresponde, desde un punto de vista teórico, al polígono de frecuencias cuando tenemos todos los datos de la población (en teoría, infinitos).

Una vez expuesto que, en una variable aleatoria continua, las propiedades de la misma vendrán descritas por la función de densidad, indiquemos que las probabilidades se calcularán como una integral definida: \[P(a <X<b) = \int_{a}^{b} f(x)dx\] es decir, la probabilidad de que la variable aleatoria \(X\) tome valores entre dos números \(a\) y \(b\) corresponde al área bajo la curva \(f\), el eje \(X\) y los puntos \(a\) y \(b\).

En el caso de una variable aleatoria continua, la probabilidad de cualquier punto concreto a es cero, porque no hay área bajo la curva: \[P(a<X<a)=\int_{a}^{a} f(x)dx=0.\] Esto puede sonar un poco raro, al principio. Si hablamos, por ejemplo, de la variable altura, nos podemos preguntar:

¿cuál es la probabilidad de medir \(1.72\)?

Según lo que acabamos de decir, la probabilidad de un punto es cero. ¿Qué sucede? Pues que, como se comentó al principio del tema, en la práctica realizamos una discretización de la variable continua altura.

La pregunta matemáticamente correcta sería:

¿Cuál es la probabilidad de tener una estatura mayor que \(1.72\)?

¿Cuál es la probabilidad de tener una estatura entre 2 valores \(a\) y \(b\)?

Lo que sí se podría calcular sería algo como

Probabilidad de medir entre \(1.72 -a\) y \(1.72+a\), siendo \(a\) cualquier número, aunque sea muy pequeño.

La probabilidad de un intervalo (por pequeño que sea), siempre será un número más grande que cero.

Precisamente por este hecho, cuando calculemos la probabilidad de que una variable continua tome valores entre dos números \(a\) y \(b\), podemos tener en cuenta que
\[P(a<X<b)=P(a<X\leq b)=P(a\leq X\leq b)=P(a\leq X <b),\] o sea, todas esas probabilidades dan lo mismo, porque considerar un punto más (o dos) no cuenta (al tener probabilidad cero).

“En algunos años, todas las grandes constantes de la física habrán sido estimadas y la única ocupación que quedará a los hombres de ciencia será la de refinar estas medidas al siguiente decimal”.

— Albert Michelson (1852-1931), famoso por su trabajo en la medición de la velocidad de la luz.