4.11 Propiedades de la probabilidad
A partir de las tres primeras propiedades de la probabilidad (axiomas de Kolmogorov), pueden deducirse fácilmente las siguientes:
Linda (Menos es más)
El siguiente ejemplo corresponde a una prueba realizada por Kahneman (Daniel Kahneman and Egan 2011) durante los años 70:
Se contaba a la gente que iba a realizar la prueba la siguiente historia sobre una mujer llamada Linda:
Linda tiene treinta y un años, es soltera, franca y muy inteligente. Se graduó en filosofía. De estudiante le preocupaban mucho los asuntos de discriminación y justicia social, y también participó en manifestaciones antinucleares.
Ahora, a los participantes de la prueba se les proponía elegir, de entre las siguientes afirmaciones, aquella que pareciese más probable sobre la descripción dada. Linda es profesora de primaria.
Linda trabaja en una librería y recibe clases de yoga.
Linda milita en el movimiento feminista.
Linda presta asistencia social en psiquiatría.
Linda es reparadora de calderas.
Linda es cajera de un banco.
Linda es corredora de seguros.
Linda es cajera y activista del movimiento feminista.Linda encaja muy bien en el tipo de la feminista activa, bastante bien en el de alguien que trabaja en una librería y recibe clases de yoga, y muy poco en el de la cajera de un banco o en el de la corredora de seguros.
Centrémonos ahora en los ítems críticos de la lista: ¿parece Linda más una cajera de banco o una cajera de banco que milita en el movimiento feminista? Cualquiera estará de acuerdo en que Linda se ajusta más a la idea de una «cajera de banco feminista» que al estereotipo de las cajeras de banco. La cajera de banco, a priori, no es una militante feminista, y añadir este detalle a la descripción hace que la historia sea más coherente.
Piénsese en términos de los diagramas de Venn. El conjunto de las cajeras de banco feministas está enteramente incluido en el conjunto de las cajeras de banco, pues cada cajera feminista es una cajera más. Por consiguiente, la probabilidad de que Linda sea una cajera feminista tiene que ser más baja que la de que sea una cajera de banco. Si especificamos un posible suceso con mayor detalle, solo podemos bajar su probabilidad. El problema crea así un conflicto entre la intuición y la lógica de la probabilidad.
Nadal va a jugar un partido. Decir cuál es el suceso más probable
A. Nadal perderá el primer set.
B. Nadal perderá el primer set, pero ganará el partido.
C. Nadal ganará el primer set, pero perderá el partido.De nuevo, a primera vista, podríamos tender a afirmar que el suceso más probable es el B, pero B está contenido en el suceso A (A es B con una condición más). Así que la probabilidad de B es menor o igual que la de A (la opción C, que Nadal pierda, no se contempla, desde luego).
La probabilidad de que llueva el fin de semana es que llueva el sábado o el domingo, o que llueva los dos días: \[P(A\cup B)=P(A)+P(B)-P(A\cap B) =0.6+0.7-P(A\cap B).\]
Como vemos, si sólo consideramos el sábado y el domingo aisladamente, la probabilidad daría más que uno, algo imposible. La posibilidad de que lluevan los dos días y no uno solo hace que debamos restar la probabilidad de la intersección, que por ahora no sabemos calcular, y que veremos en breve.
```
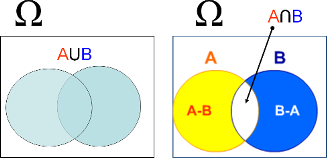
Figura 4.20: Diagrama de Venn de la unión e intersección de sucesos: la probabilidad de la unión es la suma de la probabilidad de \(A\) y la probabilidad de \(B\), pero hay que restar la probabilidad de la intersección, puesto que, en otro caso, la contaríamos dos veces.
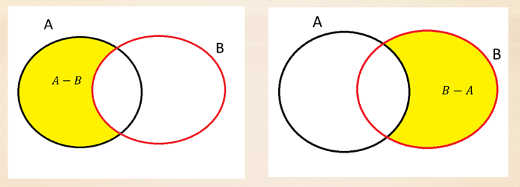
Figura 4.21: Diagrama de Venn de la diferencia de sucesos.
| Artrosis | No Artrosis | Totales | |
|---|---|---|---|
| Hombres | 45 | 30 | 75 |
| Mujeres | 55 | 15 | 70 |
| Totales | 100 | 45 | 145 |
La probabilidad de que un paciente tenga artrosis es: \(P(A)=100/145,\) y de que no la tenga es \(P(\overline{A})=1-(100/145)\)
La probabilidad de que un paciente tenga artrosis o sea una mujer es \[P(A\cup M)=P(A)+P(M)-P(A\cap M)=\frac{100}{145} +\frac{70}{145} -\frac{55}{145}\]
Probabilidad de que un paciente sea hombre y no tenga artrosis: \[P(H-A)=P(H)-P(H\cap A)=\frac{75}{145}-\frac{45}{145}=\frac{30}{145}=P(H\cap \overline{A})\]
(de que no soy el único que inventa problemas estrambóticos)
References
Kahneman, Daniel, and Patrick Egan. 2011. Thinking, Fast and Slow. Vol. 1. Farrar, Straus; Giroux New York.