Capítulo 5 Variables aleatorias
En los temas 1 y 2 hemos visto como analizar un conjunto de datos. La metodología general consiste en, a partir de una muestra de una población, resumir el contenido de esa muestra mediante análisis gráficos y numéricos.
La muestra, habitualmente, consiste en una serie de variables (numéricas o no), que llamamos variables estadísticas. Esta variable es la medición u observación de una característica concreta (estatura, peso, color… ) en cada uno de los individuos de la muestra.
Centrémonos ahora en variables numéricas. Si en vez de referirnos a los valores de la variable en una muestra concreta (que es una parte de una población) nos referimos a los valores de la variable en TODA la población, tendremos una variable aleatoria.
Recordemos, antes de nada, el esquema de trabajo de la estadística matemática (Figura 5.1):
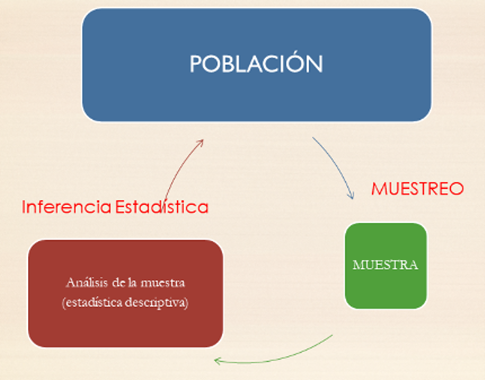
Figura 5.1: Proceso científico del análisis estadístico.
El objetivo es conocer lo mejor posible una población, a partir de una muestra de individuos. Para ello se elige una muestra de la población, lo más representativa posible de la misma, y se analiza, extrayendo toda la información que se pueda.
Para poder extrapolar los resultados de la muestra a la población, necesitaremos extender los conceptos vistos de una variable estadística a la población general.
La variable en la población general se llama variable aleatoria.
altura, peso, temperatura, etc., son ejemplos de variables aleatorias.
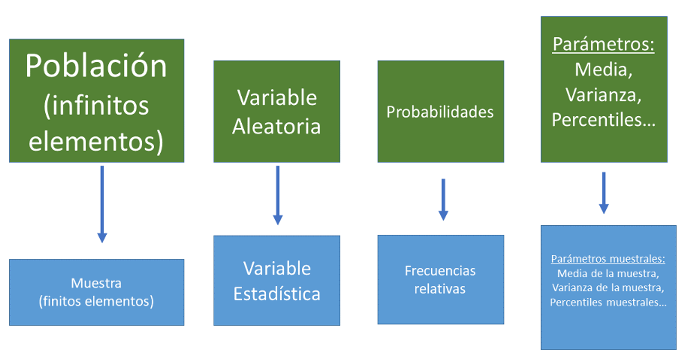
Figura 5.2: Esquema general de relación entre variables aleatorias y estadísticas.
El nombre de variable aleatoria hace referencia a que los valores de esta variable dependen del azar, mediante alguna ley concreta. El proceso de comprensión o interpretación matemática de esa aleatoriedad es el que realizaremos en este tema.