5.9 Variables aleatorias continuas notables

Como en el caso de las variables discretas, particularizamos ahora algunas variables continuas que se emplean habitualmente más que otras, y por eso también poseen nombre propio. La variable aleatoria continua más conocida y utilizada es la variable normal, que, por sus peculiaridades, merece un capítulo aparte (el siguiente). De forma análoga al caso anterior, ahora únicamente comentamos un par de ejemplos (distribución uniforme y distribución exponencial), y remitimos al querido lector a cualquier otro manual de estadística (incluído el mío, que ya no pongo cita porque a estas alturas se sabrá a cuál me refiero) para profundizar en estas variables y en otras (variable beta, gamma, Weibul…). En los casos particulares de las leyes de potencias y de la distribución normal, creo, sin embargo, que se ha efectuado aquí un resumen exhaustivo bastante amplio (en el caso de la distribución normal dudo que se encuentre otro parecido, y no por la calidad -que se da por supuesta-, sino por lo extenso).

5.9.1 Variable uniforme continua

Una variable aleatoria continua \(X\) se dice que sigue una distribución uniforme entre dos valores \(a\) y \(b\) (se representa \(X\in U(a,b))\) si su función de densidad tiene la siguiente expresión: \[f(x)= \frac{1}{b-a}, \ x\in [a,b]\] y vale 0 en cualquier otro caso.

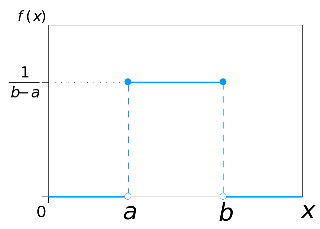
función de densidad de una variable aleatoria uniforme entre a y b.

Figura 5.13: función de densidad de una variable aleatoria uniforme entre a y b.

Esta variable es la generalización, al caso continuo, de la variable uniforme discreta (la que da a todos los valores la misma probabilidad). La variable uniforme reparte de manera continua y equivalente la probabilidad, es decir, intervalos de igual longitud (dentro de \([a,b]\)) tienen igual probabilidad.

Recuérdese que, en las variables continuas, la probabilidad entre 2 puntos \(v_1\) y \(v_2\) es el área bajo la función de densidad. En este caso, el área sería el área de un rectángulo, es decir: \[ P(v_1<X<v_2 )=\int_{v_1}^{v_2} f(t)dt=(v_2-v_1 )\cdot \frac{1}{b-a} \]

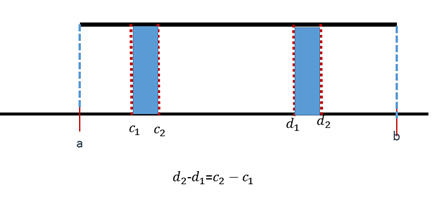
Intervalos con la misma longitud tienen la misma probabilidad (área).

Figura 5.14: Intervalos con la misma longitud tienen la misma probabilidad (área).

Gráficamente, está claro que intervalos de igual longitud tienen el mismo área y, por lo tanto, igual probabilidad. Matemáticamente, también es muy simple:

\[ \int_{c_1}^{c_2} f(t)dt=(c_2-c_1 )\cdot \frac{1}{b-a} =\int_{d_1}^{d_2} f(t)dt=(d_2-d_1 )\cdot \frac{1}{b-a} \]

5.9.1.1 Media y Varianza

Puede comprobarse que \(E(X)=\dfrac{a+b}{2}\) y \(Var(X)=\dfrac{(b-a)^2}{12}.\) Es decir, el valor medio es el punto medio del segmento o intervalo \((a,b)\), lo cual coincide con lo que nos diría la intuición: un reparto uniforme de probabilidad supone que la media esté en el punto medio.

Un estudiante llega a la parada del bus justo cuando este acaba de marcharse. El siguiente tardará en llegar como mínimo una hora, y puede llegar en cualquier momento en el transcurso de la hora siguiente. ¿Cuál es la probabilidad de que el estudiante tenga que esperar más de una hora y cuarenta y cinco minutos?

Solución

El tiempo que tarda en llegar el bus es una variable uniforme \(X\in [60,120]\). La probabilidad de que tarde más de 45 minutos en llegar (pasada la primera hora) es \(P(X>60+45)=0.25\).

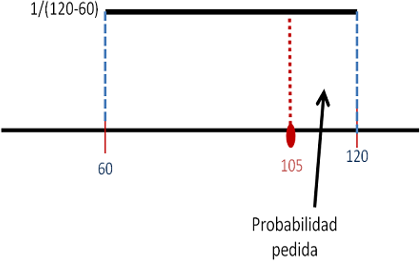
La probabilidad es el área del rectángulo que va desde 105 a 120.

Figura 5.15: La probabilidad es el área del rectángulo que va desde 105 a 120.

Cuando en R generamos números aleatorios entre 0 y 1 (o entre 2 números cualesquiera), estamos trabajando con una variable aleatoria uniforme.

La siguiente línea de código, por ejemplo, genera 10 números aleatorios con distribución uniforme entre 0 y 1.

X=runif(10,0,1) 
X
##  [1] 0.8496 0.3453 0.5000 0.1608 0.3103 0.4995 0.8649
##  [8] 0.5457 0.3344 0.5826

Vemos que nos aparecen, en efecto, 10 números entre 0 y 1. Si en vez de 10 números generamos unos cuantos más, por ejemplo, 2000, y hacemos un histograma o una estimación de la densidad, veremos que se parece a la densidad de la distribución uniforme.

X=runif(2000,0,1)
datos=data.frame(X)
histogram(~X, data=datos,   
          col="snow3", dcol="mediumblue", 
          h=1, type='density', 
          width=0.05, lwd=2 )

5.9.2 Variable exponencial

Una variable continua \(X\) se dice que sigue una distribución exponencial de parámetro \(\lambda\) (siendo \(\lambda\) cualquier número real mayor que cero) si su función de densidad es: \[f(x)= \lambda \cdot e^{-\lambda \cdot x},\ x>0\] y vale cero en cualquier otro caso (es decir, la variable exponencial solo toma valores positivos).

Se escribe \(X \in Exp(\lambda).\)

Puede comprobarse que, independientemente de cuánto valga \(\lambda\), la integral \(\int_0^{\infty} \lambda \cdot e^{-\lambda \cdot x}dx=1.\)

En la siguiente gráfica dibujamos la forma de la función de densidad para 3 valores diferentes de \(\lambda\):

### Exponencial
curve(dexp(x, rate = 0.5), xlim = c(0, 4), ylim = c(0, 2), 
  xlab = "x", ylab = "Función de densidad")
curve(dexp(x, rate = 1), col = "red", lty = 3, add = T)
curve(dexp(x, rate = 2), col = "blue", lty = 4, add = T)
abline(h = 0, col = "gray")
legend("topright", c("Exp(0.5)", "Exp(1)", "Exp(2)"), col = c("black", 
  "red", "blue"), lty = c(1, 3, 4), bty = "n")
Gráficas de la densidad de la variable exponencial.

Figura 5.16: Gráficas de la densidad de la variable exponencial.

Existen numerosos ejemplos de variables que siguen esta ley. La duración de componentes electrónicos, baterías, células en enfermedades, tienen este tipo de comportamiento: los valores más altos son mucho menos probales que los valores más bajos.

El tiempo de espera, en muchas ocasiones, también sigue una distribución exponencial: tiempo en ser atendidos en una cola en una ventanilla, tiempo entre la llegada de dos taxis a una parada…

La magnitud de los terremotos que se producen en una determinada región sigue, por regla general, una distribución de este tipo. En la terminología de seísmos, se le conoce como ley de Gutenberg-Richter. También es una ley de este tipo la que rige la velocidad de los vientos que atraviesan una determinada región. La idea básica es que terremotos (o huracanes) de magnitudes bajas hay muchos más (por suerte) que terremotos con magnitud alta.

También se verifica que la duración de las relaciones entre parejas sigue una distribucion exponencial: hay muchas parejas que duran poco y pocas que duran mucho (Newman 2005).

El físico (además de matemático y pacifista) británico Lewis Fry Richardson (1881-1953) acumuló datos de las estadísticas de “disputas mortales”, en las que incluyó la guerra entre los tipos de asesinatos. Observó que existía una especie de ley de Gutenberg-Richter de los conflictos en la que todos los acontecimientos, desde el asesinato de una persona (“conflictos de magnitud \(0\)”) a las dos guerras mundiales (“magnitud \(7\)”), obedecían a una distribución de probabilidades también de este tipo.

5.9.2.1 Media y Varianza

Puede comprobarse que \(E(X)=\dfrac{1}{\lambda}\) y \(Var(X)=\dfrac{1}{\lambda ^2}.\)

La duración media de una prótesis de cadera se estima en 20 años. La duración se corresponde con una variable aleatoria de tipo exponencial.

En este caso, al ser la media \(20\), tenemos que \[E(X)=\frac{1}{\lambda} = 20 \longrightarrow \lambda = \frac{1}{20}=0.05\] De acuerdo con esto, podemos calcular probabilidades del tipo probabilidad de que la prótesis dure como mínimo r años como \[P(X>r)=1-P(X\leq r)=1-(1-e^{-\lambda \cdot r})= e^{-\lambda \cdot r}\] Aquí hemos utilizado que la probabilidad acumulada \[P(X\leq r)=\int_0^{r} \lambda \cdot e^{-\lambda \cdot t}dt=1-e^{-\lambda \cdot r}\] mediante integración por partes.

Si, por ejemplo, \(r=25\), la probabilidad de que una prótesis dure más de 25 años será \[P(X>25)= e^{-0.05 \cdot 25}=0.28\] Todo esto último son muchas matemáticas. Obviamente, con R es mucho más simple:

pexp(25, rate=0.05)
## [1] 0.7135

nos da la probabilidad acumulada en el valor \(25\) para una distribución exponencial de parámetro \(\lambda\) (rate) igual a \(0.05.\)

Comparemos la media de una variable exponencial con la media de una variable uniforme. En la variable uniforme, la media es el punto medio. Sin embargo, en el caso que estamos considerando, la vida media de una prótesis de cadera es \(20\) años, pero este valor no deja igual probabilidad a cada lado (si lo hiciera, la media coincidiría con la mediana). Veamos qué area o probabilidad deja a la derecha el valor \(20\). \[P(X>20)= e^{-0.05 \cdot 20}=0.3678,\] lo que significa que deja \(36.78\) por ciento del área a la derecha (\(1-36.78=63.22\) a su izquierda). Por lo tanto, la media es el percentil 63, aproximadamente.

5.9.3 Las leyes de potencias (power law)

Sobre este apartado, gran parte de la información se ha extraído del trabajo de (Clauset, Shalizi, and Newman 2009).

La distribución exponencial es un caso particular de lo que se conoce como leyes de potencias. Matemáticamente, una variable \(X\) sigue una ley de potencias si su función de densidad es de la forma \[f(x)\propto x^{-\alpha },\] donde \(\alpha\) es el parámetro de escala, que habitualmente cae entre 1 y 3, aunque puede haber excepciones. El símbolo \(\propto\) significa proporcional (por ejemplo, la densidad exponencial \(e^{-x}\) es de este tipo, pues \(e^{-x}\propto x^{-2}\)) (de manera aproximada, podemos decir que los dibujos de ambas funciones son prácticamente similares).

En la práctica, pocos fenómenos empíricos obedecen las leyes de potencias para todos los valores de \(x\). En general, la ley de potencias se aplica a partir de un valor mínimo \(x_{min}\). En tal caso, se dice que la cola de la distribución sigue una ley de potencias. Estas distribuciones se llaman heavy-tail distributions (colas pesadas). Significa que su cola (habitualmente a la derecha) es descendente, pero de forma muy pausada, es decir que pueden aparecer valores extremadamente grandes y muy alejados del valor modal o del valor mediana.

La probabilidad de que \(X\) sea mayor que un número \(x\) viene dada por: \[Pr(X>x) = \begin{cases} \left(\frac{x_\mathrm{min}}{x}\right)^\alpha & \text{si }x\ge x_\mathrm{min}, \\ 1 & \text{si } x < x_\mathrm{min}. \end{cases}\]

5.9.3.1 La ley de Pareto y la regla 80-20

Uno de los ejemplos más conocidos es el relativo a la distribución de la riqueza de un país. En este caso, el parámetro \(\alpha\) es conocido como índice de Pareto. Esto se debe a que, en 1897, Vilfredo Pareto (1848-1923) afirmó que las rentas hacia el extremo más rico del espectro social están distribuidas de acuerdo a una ley de potencias. Esto implica que una gran parte de la riqueza de la nación está en manos de unos pocos individuos. En general, los porcentajes son del tipo \(80-20\), es decir el \(20\) por ciento de unos pocos poseen el \(80\) por ciento de la riqueza, mientras que el \(80\) por ciento restante solo tiene el \(20\) por ciento. Este tipo de regla \(80-20\) también se da en otras situaciones, como vamos a ver (buscad en google “regla 80 20” y encontraréis mucha más información y curiosidades).

En la gráfica de los salarios de España en 2015 se ve perfectamente esta forma. El valor modal del salario (el más frecuente) es 16.498 euros. El valor mediana es \(19.466\). Vemos que a partir de algún valor cercano a \(30.000\) o \(40.000\) euros brutos anuales la cola desciende pero lo hace muy pausadamente, puesto que hay personas que pueden ganar mucho más que la mayoría, pero son pocas. El cálculo del valor exacto \(x_{min}\) a partir del cual la cola de la distribución sigue una ley de potencias es un problema matemático con una cierta complejidad (Resnick 2007).

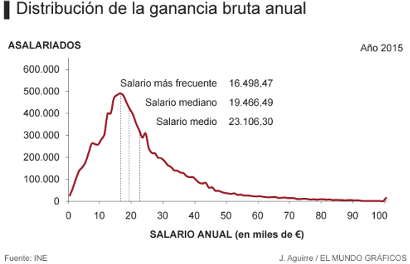
Gráfica del INE de los salarios en 2015 en España. Puede observarse una forma de tipo exponencial o ley de potencias a partir del salario medio, aproximadamente.

Figura 5.17: Gráfica del INE de los salarios en 2015 en España. Puede observarse una forma de tipo exponencial o ley de potencias a partir del salario medio, aproximadamente.

Como estas cosas, al principio, siempre suenan bastante raras, busqué por youtube algún video que lo resumiera, y encontré (entre muchos) los dos siguientes.

En este se centran, fundamentalmente, en la regla \(80-20\), la ley de Pareto y la economía.

Este seguramente nos llame la atención desde el principio:

5.9.3.2 Otras leyes de potencias

Una variable aleatoria que siga una ley de potencias puede ser tanto continua como discreta. Hemos visto cual es su función de densidad si la variable es continua. Si es discreta, su ley de probabilidad es \(P(X=x)=C\cdot x^{-\alpha }\) para \(x> x_{min}\).

Seguramente todos hemos oído hablar de leyes de este tipo en algún momento. El tamaño de los grupos de amigos, por ejemplo. Habitualmente, hay mucha gente que tiene pocos amigos y poca gente que tiene muchos. Muchos novelistas que tienen pocos lectores y pocos novelistas que tienen muchos. Muchos trabajos científicos son poco o escasamente leídos, y unos pocos son leídos o consultados por muchos…

Una representación muy habitual de las leyes de potencias es un diagrama llamado log-log plot. Es un gráfico en el que, en el eje horizontal, se representa la variable \(X\) en escala logarítmica, y en el eje vertical el logaritmo de \(1-F(x),\) que corresponde a la probabilidad \(P(X>x)\). De esta forma, se obtiene una función descendente. En cierto momento, ese descenso se convierte en una línea recta, cuya pendiente (salvo el signo) corresponde al índice \(\alpha\) de la ley de potencias.

Veamos un ejemplo con una variable exponencial (las unidades del gráfico son logarítmicas, pero aparecen las originales para facilitar la interpretación del mismo).

Distribución exponencial, representada mediante su función de densidad, y mediante un grafico log-log.

Figura 5.18: Distribución exponencial, representada mediante su función de densidad, y mediante un grafico log-log.

En (Clauset, Shalizi, and Newman 2009) se detallan los siguientes ejemplos (ver a continuación las Figuras 8 y 9 del artículo) de casos empíricos reales que se ajustan a una ley de potención:

  1. La frecuencia de aparición de palabras únicas en la novela Moby Dick (Herman Melville).
  2. Los grados (es decir, el número de compañeros de interacción distintos) de las proteínas, en la red de interacción proteica de la levadura Saccharomyces cerevisiae.
  3. Los grados de metabolitos en la red metabólica de la bacteria Escherichia coli.
  4. Los grados de nodos en la representación de la red de Internet en mayo de 2006.
  5. El número de llamadas recibidas por los clientes de la compañía telefónica AT&T, en los Estados Unidos, durante un solo día.
  6. La intensidad de las guerras entre 1816 y 1980, medida como el número de muertos en combate por cada 10.000 habitantes de las naciones en guerra.
  7. La gravedad de los atentados terroristas perpetrados en todo el mundo, entre febrero de 1968 y junio de 2006, medida como el número de muertes directamente resultantes.
  8. El número de bytes de datos recibidos -como resultado del comando http- en un gran laboratorio de investigación, durante las 24 horas del día en junio de 1996. En términos generales, esta distribución representa la distribución del tamaño de archivos web transmitidos a través de Internet.
  9. El número de especies por género de mamíferos. Este conjunto está compuesto principalmente de especies vivas hoy en día, pero también incluye algunas especies recientemente extinguidas, donde “reciente” en este contexto significa “en los últimos miles de años”.
  10. El número de avistamientos de aves de diferentes especies en América del Norte en el año 2003.
  11. El número de clientes afectados por cortes de electricidad en los Estados Unidos entre 1984 y 2002.
  12. El número de copias de los libros más vendidos en los Estados Unidos durante el período de 1895 a 1965.
  13. La población de las ciudades en el Censo de los Estados Unidos del año 2000.
  14. El tamaño de las libretas de direcciones de correo electrónico de los usuarios de una universidad.
  15. El tamaño en acres de los incendios forestales que ocurrieron en tierras federales de EE.UU. entre 1986 y 1996.
  16. Intensidad máxima de rayos gamma de las erupciones solares entre 1980 y 1989.
  17. La intensidad de los terremotos que ocurrieron en California entre 1910 y 1992.
  18. El número de seguidores de religiones y sectas, según consta en el sitio web adherents.com.
  19. La frecuencia de ocurrencia de apellidos en los Estados Unidos en el censo de 1990.
  20. El patrimonio neto agregado en dólares de los individuos más ricos de los Estados Unidos en octubre de 2003.
  21. El número de citas recibidas por los artículos científicos del Science Citation Index entre 1981 y 1997.
  22. El número de trabajos académicos escritos o co-escritos por matemáticos en la base de datos MathSciNet de la Sociedad Matemática Americana.
  23. El número de “hits” recibidos por los sitios web de AOL en un sólo dia.
  24. El número de enlaces a sitios web, encontrados en un rastreo de la Web en 1997, de unos 200 millones de páginas web.
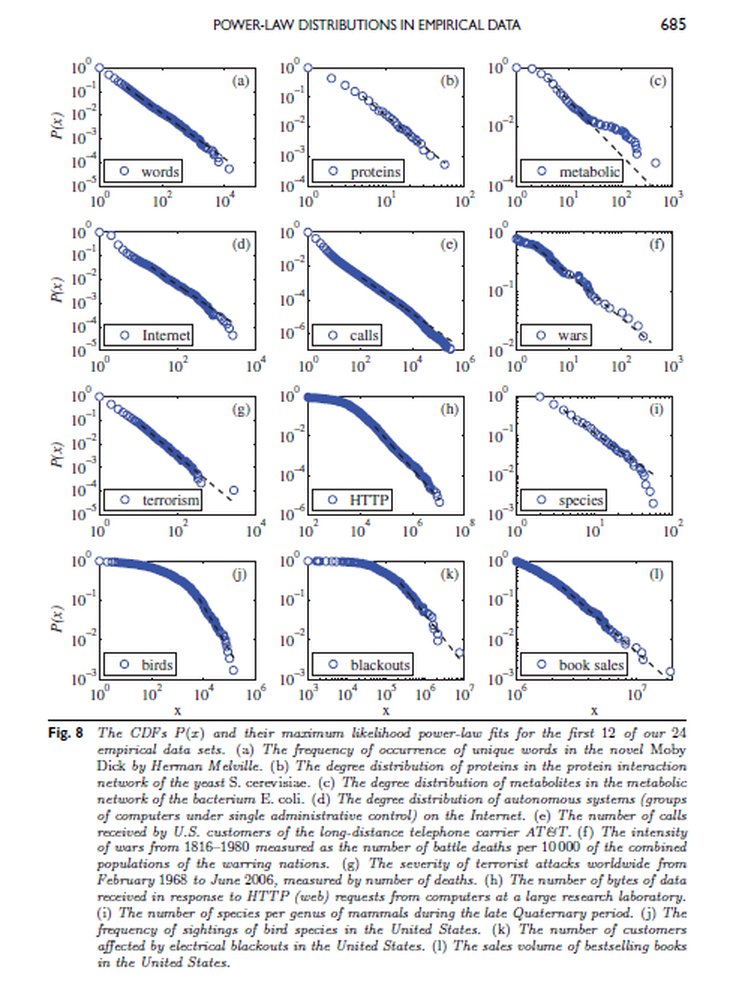
Figura 8 del trabajo de Clauzet, Shalizi y Newman (2009).

Figura 5.19: Figura 8 del trabajo de Clauzet, Shalizi y Newman (2009).

Figura 9 del trabajo de Clauzet, Shalizi y Newman (2009).

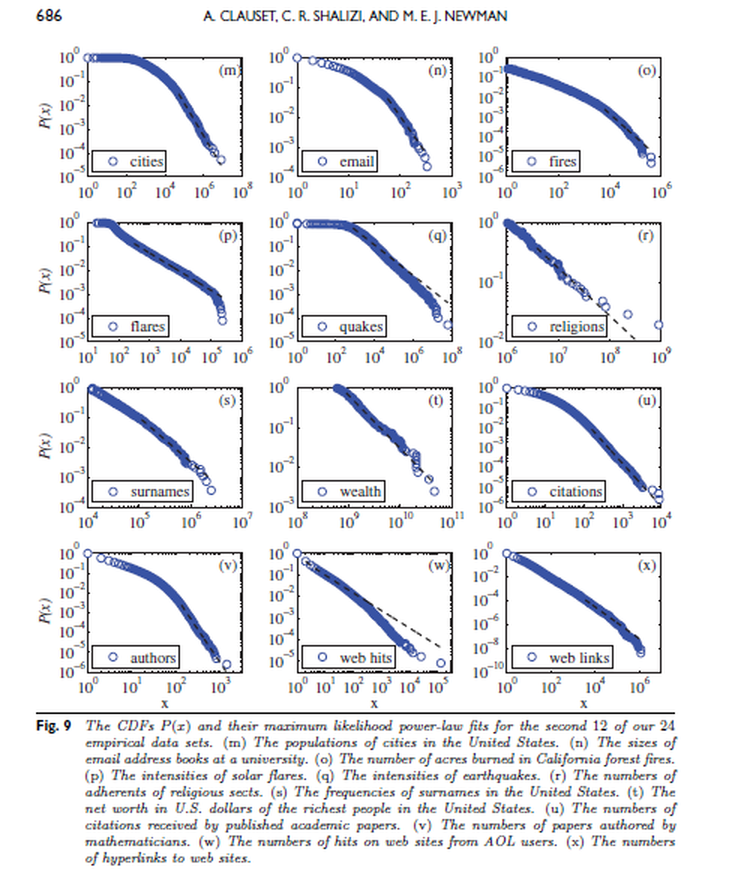
Figura 5.20: Figura 9 del trabajo de Clauzet, Shalizi y Newman (2009).

References

Clauset, Aaron, Cosma Rohilla Shalizi, and Mark EJ Newman. 2009. “Power-Law Distributions in Empirical Data.” SIAM Review 51 (4). SIAM: 661–703.

Newman, Mark EJ. 2005. “Power Laws, Pareto Distributions and Zipf’s Law.” Contemporary Physics 46 (5). Taylor & Francis: 323–51.

Resnick, Sidney I. 2007. Heavy-Tail Phenomena: Probabilistic and Statistical Modeling. Springer Science & Business Media.