Capítulo 6 La Variable Normal o Gaussiana
En este trozo del documental de la 2 al este de la campana de Gauss (puede encontrarse en la web de TVE) nos hablan un poco de la historia del que fue niño prodigio Karl Fiedrich Gauss, apodado el príncipe de las matemáticas.
Gauss no fue el inventor de la campana (función de densidad de la variable normal), pero esta lleva su nombre en su honor. El concepto normal es sinónimo aquí de común, de general, como opuesto a lo atípico o poco probable. Esta concepción tiene a su vez un desarrollo histórico no sin interés. Sin embargo, para la introducción de la variable, el nombre resulta más que adecuado, a partir de la gran cantidad de ejemplos que veremos a continuación. La ley normal, también llamada ley de los errores, fue utilizada por primera vez en 1733, cuando de Moivre la propuso como aproximación de la distribución binomial. En 1783, Laplace la propuso para describir la distribución de los errores accidentales en la medición de una magnitud física. El termino “ley normal” no aparece hasta 1894, de la mano, precisamente, de Karl Pearson (Porter 1986).
“No se me ocurre nada tan propenso a impresionar la imaginación como la maravillosa forma de orden cósmico expresada por la ley del error (la curva de Gauss). Si un salvaje la hubiera comprendido, le habría rendido culto como a una divinidad. Cuanto más grande es la multitud y mayor la anarquía aparente, mas perfecto es su dominio. Es la ley suprema de la sinrazón: siempre que una muestra grande de elementos caóticos juegan un papel similar en magnitud, emerge una forma insospechada y bella de regularidad, presente en estado latente desde el principio”.
— Sir Francis Galton
Unos años después de escribir este párrafo tan rimbombante (¿Quién dijo que la mejor lírica y las matemáticas son incompatibles?), Galton escribió una versión 2.0 de la misma, quizá más politicamente correcta. Sustituyó “Si un salvaje […] divinidad” por “Los griegos, de haberla conocido, la habrían divinizado”.
De manera general, una variable aleatoria continua \(X\) se dice que sigue una distribución normal o gaussiana de parámetros \(\mu\) y \(\sigma\) si su función de densidad es de la forma: \[f(x)=\dfrac{1}{\sigma \sqrt{2\pi }}e^{-\dfrac{(x-\mu )^2}{2\sigma ^{2}}},\ \ -\infty <x<\infty \]
Se verifica que \[ E(X)=\int_{-\infty }^{\infty } xf(x)dx = \mu, \ \ \ Var(X)=\int_{-\infty }^{\infty } (x-\mu )^2f(x)dx = \sigma^2\] esto es,
La función de densidad es simétrica respecto de la media \(\mu,\) es decir, áreas a la derecha y a la izquierda (probabilidades) coinciden. Las áreas entre valores de \(\mu -k\sigma\) y \(\mu +k\sigma \ (k=1,2,3)\) pueden verse en la siguiente gráfica, llamada la campana de Gauss.
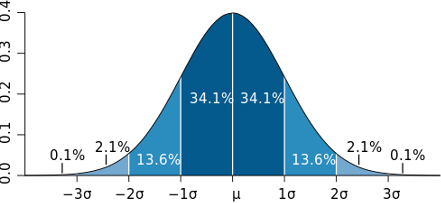
Figura 6.1: La campana de Gauss presenta simetría y la misma distribución de áreas, independientemente de cuáles sean sus párametros media y desviación típica.
Esta variable, cuando se consideran los valores \(\mu=0\) y \(\sigma=1\), se llama Normal estándar o Normal tipificada.
Si tenemos una variable \(X\) con media \(\mu\) y desviación típica \(\sigma\), a partir de ella se puede construir lo que se conoce como variable tipificada o estandarizada \(Z=\dfrac{X-\mu}{\sigma}\), verificándose que esta variable \(Z\) tiene media cero y desviación típica uno.
Esta propiedad resultaba de mucha importancia hasta hace unos años, cuando había que calcular probabilidades de esta variable “a mano”, y se utilizaba siempre la llamada tabla de la distribución normal, que es una tabla con probabilidades (áreas) de la distribución normal estándar, de media cero y desviación típica 1. Gracias a la propiedad de estandarización de cualquier variable normal, se pueden calcular las probabilidades asociadas a dicha variable tipificando la misma.
References
Porter, Theodore M. 1986. The Rise of Statistical Thinking, 1820-1900. Princeton University Press.