2.8 Medidas características de una variable
Una vez organizados los datos en su correspondiente distribución de frecuencias, procedemos a dar una serie de medidas que resuman, de la mejor forma posible, la información existente en los mismos y que, de alguna manera, representen a la distribución en su conjunto. El interés se centra en proporcionar un número reducido de valores que caracterizen bien, o lo mejor posible, el conjunto de datos, por grande que este sea. Hay tres tipos fundamentales: medidas de posición (centro), medidas de dispersión (variabilidad) y medidas de forma.
El objetivo, a partir de un conjunto de datos, que puede ser muy grande, es obtener un conjunto pequeño de números que resuman bien el conjunto de datos. No deja de resultar curioso que, para describir la información, reduzcamos la misma. Pero veremos que, en efecto, con un conjunto pequeño de valores podemos resumir bastante bien a un conjunto muy grande.
2.8.1 Medidas de posición o de tendencia central
De alguna manera, estas medidas centralizan la información, y por ello se llaman de tendencia central o promedios. Con ellas, se pretende también facilitar la comparación entre distintas variables.
2.8.1.1 La media (media aritmética)
La media es una medida de representación o de tendencia central que se define de la siguiente manera:
\[ x=\frac{x_{1}+x_{2}+...+x_{n}}{n}.\]
La nota media de los exámenes de una asignatura, el tiempo medio de realización de los mismos, la estatura media, la ganancia media en comisiones ilegales, etc.
En R, para calcular la media de una variable se utiliza mean(variable).
X=c(2,3,4,4.5,4.5,5.6,5.7,5.8,6,6.1,6.5)
mean(X)## [1] 4.8822.8.1.1.1 Características esenciales de la media aritmética
- Si a partir de una variable \(X\) creamos otra \(Y=aX+b,\) entonces la media de la nueva variable es \(\overline{y}=a\overline{x}+b\)
Supongamos que han salido las notas de una asignatura, y la nota media es \(2.5\). Para no tener que rellenar cien mil papeles explicando por qué los alumnos son tan desastrosos, el profesor decide subir la nota a todo el mundo en 3 puntos.
Obviamente, si la nota más alta era, por ejemplo, un \(5\), ahora será \(8\). Si la nota más baja era un cero, ahora será \(3\), y parece lógico que la nueva media sea \(5.5\).
Si el profesor hubiera considerado, en vez de sumar \(3\) puntos, multiplicar cada nota por \(3\), ahora la nota más alta sería \(15\), y la nota media \(7.5\).- La media aritmética se ve muy alterada por valores extremos de la variable. Supongamos, por ejemplo, que una variable toma los valores \(X=1,4,12.\) Su media es \(\overline{X}=5.66.\) Si añadimos un nuevo valor, por ejemplo \(100,\) ahora la media es \(\overline{X}=29.25.\) Es decir, valores grandes de \(X\) desplazan la media hacia la derecha. Lo mismo ocurre con valores pequeños de \(X,\) que desplazan la media hacia la izquierda (Figura 2.23).
Figura 2.23: Esta propiedad la conocen perfectamente los chavales.
Esta afectación de la media aritmética por valores extremos se explica por el significado que tiene la misma desde el punto de vista de la física: la media aritmética representa el centro de gravedad de la distribución de los datos. Si los datos son pesos, la media aritmética deja igual peso a un lado que al otro, por eso se desplazaría hacia los lados con valores extremos (Figura 2.24),
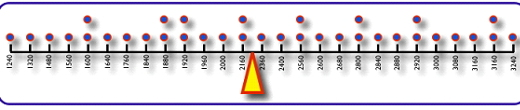
Figura 2.24: Datos=Pesos. La media aritmética es el centro de gravedad.
2.8.1.2 Media recortada
La Media recortada (media \(\alpha\)-trimmed) a un nivel \(\alpha\) es la media aritmética, calculada quitando el \(\alpha\) por ciento de los datos inferiores y superiores.
# Para calcular la media recortada de una variable
# se utiliza mean(Variable, trim= 0 a 0.5)
X <- c(0:10, 50)
mean(X, trim = 0.10)## [1] 5.5#frente a
mean(X)## [1] 8.752.8.1.3 La media ponderada
Consiste en asignar a cada valor \(x_{i}\) un peso \(w_{i}\), que dependerá de la importancia relativa de dicho valor, bajo algún criterio. Su expresión responde a:
\[ x_{p}=\frac{x_{1}⋅w_{1}+x_{2}⋅w_{2}+...+x_{n}⋅w_{n}}{w_{1}+w_{2}+...+w_{n}}.\]
wt <- c(5, 5, 4, 1)/15
x <- c(3.7,3.3,3.5,2.8)
xm <- weighted.mean(x, wt)
xm## [1] 3.4532.8.1.4 Otras medias
Son, por ejemplo, la media geométrica o la media armónica, esta última interesante puesto que es la media entre velocidades (en general, es la media resultante cuando las unidades son proporciones, como la velocidad que se mide en km/hora o metros/segundo). Ver, por ejemplo como consumir menos
2.8.1.5 El concepto histórico de media
2.8.1.5.1 Nominalismo, realismo, y la intervención de Occam para apoyar a los franciscanos contra el papa (siglo XIV)
La media aritmética, desde un punto de vista matemático, existe desde la época de la escuela pitagórica. Sin embargo, no tuvo ningún significado de tipo estadístico hasta el siglo XVII, cuando los astrónomos empezaron a utilizarla para dar una medida única de datos de observaciones que presentaban discrepancias. Al realizar mediciones, por ejemplo de distancias de la tierra a estrellas o entre estas, siempre solían aparecer diferencias (los aparatos de medición no eran, obviamente, los mismos que hoy en día), y se decidió, realmente sin saberse muy bien por qué, elegir como medida representativa de estas observaciones a la media aritmética.
Desde el punto de vista histórico, sin embargo, la consideración de la media aritmética como valor representativo de un conjunto tardó mucho en aparecer. Sobre este hecho, conviene destacar la posición nominalista de Guillermo de Occam (fraile franciscano, filósofo y lógico escolástico inglés; 1285-1347), relativo al voto de pobreza pronunciado en el siglo XIII por San Francisco de Asís y asignado como regla a la orden de los franciscanos.
En poco tiempo, los franciscanos prosperarían tanto que pronto comenzaron a dirigir numerosos monasterios y propiedades agrícolas. Sin embargo, para permitirle respetar, al menos nominalmente, su voto de pobreza, el Papa aceptó tomar a su cargo la propiedad de estos bienes, aunque cediéndoles el usufructo. Sin embargo, en el siglo XIV, el Papa, fatigado por la carga administrativa decide entregárselos a la orden, lo que obviamente enriquecería a esta última, pero avivaría las críticas formuladas, por una corriente opositora que reclamaba el retorno a la posición inicial del voto de pobreza de San Francisco.
En esta situación, Occam interviene para defender la posición de los franciscanos frente al papa. Argumenta que no es posible entregar los bienes a la orden considerada como un todo, ya que esto no es más que un nombre que designa a individuos franciscanos. Niega así la posibilidad de que existan personas colectivas distintas de las personas singulares, cuestión que traerá muchas consecuencias en el futuro. Así, al individualismo lógico del nominalismo se le asocia un individualismo moral, a su vez ligado a una concepción de la libertad del individuo, solo frente al Creador. (Desrosières 2004).
Esta (mas que) anécdota histórica puede servir de argumento a la imposibilidad de contemplar un único valor como representativo de un conjunto, puesto que sólo podían contemplarse características individuales, nunca en grupo. Tendremos que esperar hasta varios siglos después, cuando la ley de los grandes números de Poisson (siglo XIX) permite dar un paso importante a Quetelet (Perrot 1992). Este último, por encargo del gobierno de Francia, se ocupa de los cálculos necesarios para justificar un nuevo impuesto nacional: el diezmo real. Quetelet, para ello, necesita estimaciones variadas: la superficie, los rendimientos agricolas, las cargas fiscales… En ciertos casos, dispone de varias estimaciones de una magnitud desconocida (la superficie total del país), de la que extrae una media proporcional. En otros, en cambio, utiliza informaciones -por ejemplo, sobre los rendimientos agrícolas-, referidas a parroquias o a distintos años. Efectúa entonces un cálculo análogo al precedente, pero no le da el nombre de media, sino de valor común. La operación de adición suprime las singularidades locales y permite que surja un objeto nuevo de orden más general, eliminando las contingencias no esenciales.
2.8.1.6 La mediana
La mediana es un valor que, previa ordenación, deja la mitad de las observaciones a su izquierda y la otra mitad a su derecha. Es decir, el \(50\%\) de los datos son menores o iguales que la mediana, y el otro \(50\%\) mayores o iguales a ésta.
Para su cálculo, y suponiendo que los valores están ordenados, se procede de la siguiente manera:
Si hay un número impar de datos, la mediana es el elemento que se encuentra en el centro, es decir, el valor que ocupa el lugar \(\left( \frac{n+1}{2} \right)\).
Si el número de datos fuera par habría dos elementos centrales, y la mediana se obtendría como la media de ambos.
Sea \(X\) la variable que toma los valores \(1,2,3,4,5\) (hay \(n=5\) datos). La mediana es \(Me=3\) (deja 2 valores a la izquierda y 2 a la derecha).
Si \(X\), en cambio, toma los valores \(1,2,2,3,4,5,\) ahora hay un número par de valores. En el medio tenemos los valores \(2\) y \(3.\) La mediana es \(Me=\left( 2+3 \right) /2=2.5.\)Veamos ahora un ejemplo de película. Hablamos de Blancanieves y la leyenda del cazador (2012), en la cual no respetan demasiado el cuento, y, como vemos en la Ilustración 2.25 , salen 8 enanos en vez de 7 (parece ser que el octavo es el padre de los otros).

Figura 2.25: Blancanieves, la reina, el cazador y los enanitos.
Consideremos que todos los enanitos miden 1 metro. La mediana de los 8 datos sería 1 m. Si añadimos a Blancanieves al grupo (1.65 m), la mediana sigue siendo 1. Si añadimos a la madrastra, sigue siendo 1. Y aún añadiendo al cazador, que es un dato bastante separado de los otros (1.92), tenemos en el conjunto total 11 datos. Por lo tanto, la mediana ocupará el lugar sexto (deja 5 datos a cada lado), y sigue siendo 1. Esta propiedad que verifica la mediana, de no dejarse afectar por datos extremos, se llama robustez.
A la hora de hablar, por ejemplo, del sueldo promedio o renta media de un país, resulta evidente que debería indicarse la medida que se utiliza. Así, un sueldo medio dado por la mediana sería aquel tal que el 50 por ciento de la población tendría sueldo más bajo que la mediana, y el otro 50 por ciento un sueldo más alto que la mediana. En cambio, el sueldo media aritmética es el valor correspondiente a sumar todos los sueldos y dividir por el número de personas. Si existe poca gente con sueldos muy altos, el sueldo media aritmética puede ser alto, pero no será representativo del conjunto total de la población. Es otro ejemplo de la robustez de la mediana frente a la no robustez de la media aritmética: si hay un porcentaje de personas no muy grande con sueldo muy elevado, provoca que la media aritmética sea también elevada.
x=c(2,3,1,1,0,5,5,6,12,3,4,5,5,4,7)
Me <-median(x)
Me## [1] 4Nota histórica:
La idea de un medio o mediano (lo cual es una descripción) que sea excelente (lo cual es una evaluación) es una de las enseñanzas más familiares de Aristóteles. “La virtud es un medio entre dos vicios, uno de exceso y otro de deficiencia”. Aristóteles explícitamente restringió la aplicación del concepto de medio porque se trata de una excelencia que contrasta con el exceso o la deficiencia. “No todos los puntos medios son medios. El rencor y el adulterio, son en sí mismo bajos, y no son bajos a causa de exceso y deficiencia” (Hacking and Bixio 1995).
El concepto de mediana apareció con posterioridad al de media aritmética. Quien primero lo utilizó fue Galton, y la generalización al concepto de percentil fue hecha por Pearson.
2.8.1.7 La moda
La moda (absoluta) de una distribución es el valor que más veces se repite (el valor con mayor frecuencia o más frecuente). Además de la moda absoluta, aquellos valores que tengan frecuencia mayor a la de los valores adyacentes serán modas relativas. Por ejemplo, si tenemos la variable \(X\) que toma los valores \(2,3,3,4,6,7,7,7,10\), la moda absoluta es \(7\), puesto que es el valor que se repite más veces. Además, el valor \(3\) es una moda relativa, puesto que su frecuencia es \(2\), superior a la de los valores \(2\) y \(4\), ambas iguales a \(1.\)

Figura 2.26: Población de g.. (gente bien vestida): valores más frecuentes de abrigos, solapas y sombreros.
En el caso de una variable continua se habla de intervalo modal, que a su vez puede ser absoluto o relativo.
La moda es un valor que se ve directamente al observar el diagrama de barras si la variable es discreta, o el histograma si es continua.
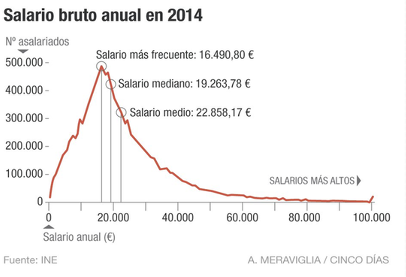
Figura 2.27: Mostramos de nuevo el gráfico de los salarios Piénsese en la diferencia entre el sueldo moda, mediana y media aritmética.
Pensemos ahora en la siguiente frase, dicha en su momento por un presidente del gobierno:
“En cuestión de financiación autonómica, todas las comunidades autónomas quedarán por encima de la media”.
— José Luis Rodríguez Zapatero
(Sí, en efecto, sé lo que estás pensando: sea cual sea la media, es imposible que todos los datos estén por encima de ella. Siempre, se trate de la medida que se trate, la media estará entre los datos, más al medio o menos al medio, pero nunca dejará todos los datos detrás o después, sino vaya porquería de media sería. Así que, por favor, no cometa usted errores como los de ciertos señores, que convierten en veraces frases como “cuanto más inútil se es, más alto se llega”).
Otra frase famosa:
“El mayor argumento en contra de la democracia son cinco minutos de conversación con el votante medio.”
— Winston Churchill, uno de los mejores políticos del siglo XX

Figura 2.28: Sir Winston Churchill, presidente inglés durante la II guerra mundial.
y fiel ejemplo de que el hombre no procede del mono, sino del perro, en este caso del bull-dog (inglés, of course).
Y el que no lo crea que vea aquí cómo hay perros más listos que muchos hombres (¿o acaso sabe usted hacer eso?)
Ahora una encuesta para saber qué opina una persona media sobre esto del salario medio:
2.8.1.8 Cuantiles o percentiles
Se llama cuantil o percentil \(p\) (o de orden \(p\)) \((0<p<100)\) a aquel valor que divide a la variable en dos partes, dejando a su izquierda (o inferiores a él) el \(p\) por ciento de los datos (a su derecha el \(100-p\) por ciento). Por ejemplo, si \(p=50\), el percentil de orden 50 corresponde a la mediana.
Generalmente, mientras los percentiles van de 1 a 100, los cuantiles se toman de 0 a 1, y es entonces lo mismo el percentil \(12\), por ejemplo, que el cuantil \(0.12\).
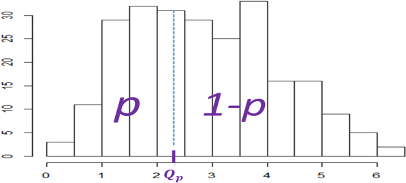
Figura 2.29: Percentil \(p\) en una variable continua.
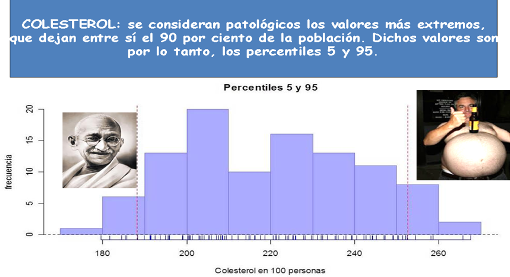
Figura 2.30: Posible uso de interes de los percentiles.
Figura 2.31: Tabla de percentiles de 2 a 20 años, por sexo, peso y estatura.
2.8.1.8.1 Cuartiles
Si consideramos los percentiles \(25, 50\) y \(75\), estos 3 valores dividen a las observaciones en cuatro partes iguales, y por eso se llaman cuartil primero, cuartil segundo y cuartil tercero. Suelen representarse por \(Q_1,Q_2\) y \(Q_3\) (Figura 2.32).
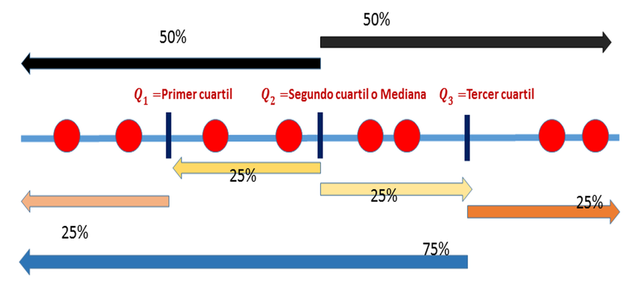
Figura 2.32: Cuartiles: Percentil 25, Mediana y Percentil 75.
2.8.1.8.2 Deciles
Igual que el caso anterior, si consideramos los percentiles \(10,20,30...\) hasta \(90\) tenemos 9 valores que dividen a las observaciones en 10 partes iguales, y esos valores se llaman deciles. Se representan como \(D_1,D_2,\dots ,D_9\).
De forma similar puede considerarse cualquier reparto de los porcentajes, pudiendo así hablarse de terciles, quintiles, etc.
Primero seleccionamos la variable peso, de los hombres blancos (entre 17 y 50 años). Vemos un sumario básico de los datos, y representamos en el histograma los cuantiles 5 y 95 (el primero deja el 5 por ciento de datos a su izquierda, y el segundo a su derecha).
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 40.4 | 74.6 | 85.6 | 88.88 | 99.4 | 187.8 |
Figura 2.33: Percentiles 5 y 95 de la variables Peso.
Este grafíco, como vemos, difiere en su aspecto con los tradicionales. Lo hemos realizado usando la libreria ggplot2, que puede crear gráficos muy bonitos, pero su creación requiere un poco de cuidado. Se puede ver una guía en el libro online (gratuito) de Kieran Healy Data visualization, en la página del grupo RNA-Seq, en la página de STHDA y, lógicamente, en el libro del autor del paquete ggplot2, Hadley Wickham (Wickham 2016).
Ahora, consideramos la variable que mide el colesterol (LDL), seleccionada en el mismo grupo de personas. Representamos sobre el histograma los cuartiles (dividen la distribución en cuatro partes iguales).
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 39 | 81.75 | 103 | 106.7 | 130 | 240 |
## 25%
## 81.75## 50%
## 103## 75%
## 130Figura 2.34: Cuartiles variable Colesterol LDL
[La gran revancha(2013)]
[Syriana (2006)]
[Como la vida misma (2010)]
2.8.2 Medidas de dispersión
[Carolina Bescansa (Podemos) refiriéndose a la baja puntuación de Pablo Iglesias en una encuesta sobre valoración de líderes políticos]
Las medidas de tendencia central reducen la información de una muestra a un único valor, pero, en algunos casos, este valor estará más próximo a la realidad de las observaciones que en otros.
Por ejemplo, consideremos la variable \(X=0,5,10\) y la variable \(Y=3,7\). Enseguida podemos ver que las medias aritméticas de ambas variables son iguales (\(\bar{X}= \bar{Y}=5\)), pero también que la variable X está más dispersa (o menos concentrada) que la variable Y, de manera que la representatividad de \(\bar{Y}\) es mayor que la de \(\bar{X}\) (Gráfica 2.35).
Figura 2.35: Dos variables con la misma media aritmética y diferente dispersión.
A continuación se estudian una serie de medidas que, por una parte, indicarán el nivel de concentración de los datos que se están analizando y, por otra, informarán sobre la bondad de los promedios calculados como representativos del conjunto de datos. Recordemos que el objetivo de la estadística descriptiva es describir lo más sucintamente posible un conjunto de datos. A través de sus valores medios, podemos tener una gran cantidad de información simplemente con unos pocos números. Lo procedente es saber qué fiabilidad nos ofrecen esas pocas cantidades o números, es decir, cuánta variabilidad existe en el conjunto de datos. Si hay poca variabilidad, la información de los valores medios será muy precisa. Si, en cambio, existe mucha variabilidad, la información será menos precisa. Esta fue, concretamente, una de las muchas aportaciones a la estadística que proporcionó Francis Galton. Ya era conocido, en su época, la aportación numérica de un valor medio (en concreto la media aritmética) a la información de un grupo de datos. Galton dijo que el paso siguiente era completar esa información cuantificado la variabilidad.
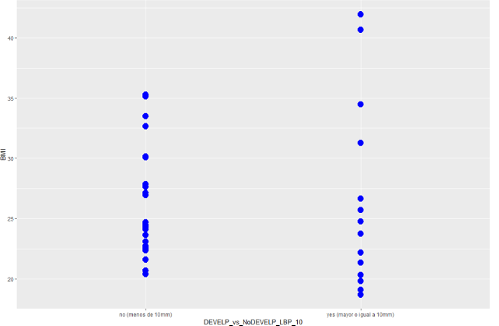
Figura 2.36: Indice de masa corporal según dolor de espalda. Variabilidad diferente según cada grupo.
2.8.3 La Varianza y la desviación típica
La varianza y su raíz cuadrada positiva, la desviación típica, son las medidas de dispersión más importantes, estando íntimamente ligadas a la media como medida de representación de ésta. La varianza viene dada por la expresión: \[ S^{2}= \sigma ^{2}=\frac{ \left( x_{1}-\overline{x} \right) ^{2}+ \left( x_{2}-\overline{x} \right) ^{2}+...+ \left( x_{n}-\overline{x} \right) ^{2}}{n}=\frac{1}{n} \sum _{i=1}^{n} \left( x_{i}-\overline{x} \right) ^{2}. \] Se utiliza esta fórmula por ser la media aritmética de la variable cuyos valores son \(\left( x_{i}-\overline{x} \right) ^{2}.\)
Es decir, estamos considerando las distancias entre los datos y la media aritmética, y las promediamos.
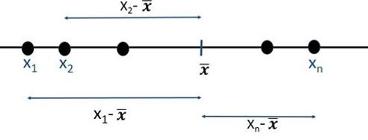
Figura 2.37: Distancias de los puntos a la media aritmética.
Supongamos que tenemos los siguientes datos: \(X= -4,-2,5,9,10,11,14.\) Calculamos su media
X=c(-4,-2,5,9,10,11,14)
media=mean(X)
# vamos a calcular las distancias
# de cada dato a la media
D=(X-media)^2
D## [1] 102.878 66.306 1.306 8.163 14.878 23.592
## [7] 61.735# La varianza es la media de esta nueva variable
mean(D)## [1] 39.84# y la desviación típica es la raiz cuadrada
sqrt(mean(D))## [1] 6.312Si las distancias entre los datos y la media, en general, son grandes, la media de estas distancias también lo será.
Si las distancias entre los datos y la media, en general, son pequeñas, la media de las distancias también lo será.
Ahora bien, las distancias \(x_{i}-\overline{x}\) las elevamos al cuadrado para evitar que se compensen las distancias positivas y negativas (según que los datos \(x_{i}\) estén a la izquierda de la media o a la derecha).
Realmente, puede demostrarse que, si no lo hacemos, y considerásemos el promedio \(\frac{1}{n} \sum _{i=1}^{n} \left( x_{i}-x \right)\) como la varianza, esto no serviría para nada, ya que ese promedio es siempre cero.
# Consideremos los mismos datos de antes
X=c(-4,-2,5,9,10,11,14)
media=mean(X)
# vamos a calcular las distancias
# sin elevar al cuadrado
D=X-media
# Si ahora calculamos la media de
# esta variable nos dará cero
mean(D)## [1] -1.27e-16La desviación típica es la raiz cuadrada, con signo positivo, de la varianza. \[\sigma =+\sqrt{\sigma^2}\] que mide la dispersión en las mismas unidades de la variable \(X\), puesto que la varianza mide la dispersión en las unidades de la variable, pero elevadas al cuadrado (si \(X\) son, por ejemplo, metros, la varianza está en metros al cuadrado, y la desviación típica de nuevo en metros).
La forma de calcular la varianza y la desviación tipica en R es con
X=c(-4,-2,5,9,10,11,14)
var(X)## [1] 46.48sd(X)## [1] 6.817Como vemos, no da exactamente lo mismo que antes. Esto es porque R considera lo que se llama cuasi-varianza \[ S^{2}_{n-1}= \frac{ \left( x_{1}-\overline{x} \right) ^{2}+ \left( x_{2}-\overline{x} \right) ^{2}+...+ \left( x_{n}-\overline{x} \right) ^{2}}{n-1}=\frac{1}{n-1} \sum _{i=1}^{n} \left( x_{i}-\overline{x} \right) ^{2}. \] El valor que se calcula con sd es la raiz cuadrada de \(S^2_{n-1}\). El motivo es de tipo teórico, puesto que si los datos son observaciones de una variable aleatoria (a definir en capítulos posteriores), este último valor representa mejor a la varianza teórica de la variable (no os preocupéis por entender este detalle en este preciso momento). En cualquier caso, si \(n\) es un número relativamente grande, los valores que se obtienen diviendo entre \(n\) o \(n-1\) son prácticamente iguales.
En las calculadoras que realizan cálculos estadísticos suele existir un botón con el símbolo \(x\sigma n\) (o algo parecido), y otro botón con el símbolo \(x \sigma\left( n-1 \right)\), indicando que el primero calcula la varianza (o desviación típica) dividiendo por \(n,\) y el segundo dividiendo por \(n-1.\)
Tanto la varianza como la desviación típica son siempre positivas, y valen cero sólo en el caso de que todos los valores coincidan con la media (representatividad absoluta de la media).
Desde el punto de vista físico, así como la media aritmética representa el centro de gravedad de una distribución, la varianza mide el momento de inercia alrededor de un eje que sería la media aritmética. Cuanto mayor es la varianza, mayor el momento de inercia. El ejemplo clásico de los patinadores que extienden los brazos para frenarse, aumentando el momento de inercia, sería un ejemplo de poca dispersión alrededor del eje. Los patinadores que encogen los brazos, en cambio, pueden girar mucho más rápido al ser la dispersión mucho menor (el que no sepa esto, o no lo entienda, que pruebe a patinar sobre el hielo y hacer giros, que es muy divertido).
2.8.4 Recorrido
Se define como la diferencia entre el mayor y el menor de los valores. Obviamente, es una medida de dispersión, y bien sencilla, además. Tiene la ventaja de que la calcula cualquiera, aunque cuando hay valores aislados en las puntas o extremos de la distribución, da una visión distorsionada de la dispersión de ésta.
\[ Recorrido=Max \left( X \right) -Min \left( X \right).\]
2.8.5 Recorrido intercuartílico.
Viene dado por:
\[ R_{I}=Q_{3}-Q_{1}.\] donde \(Q_{3}\) y \(Q_{1}\) son el tercer y primer cuartil, respectivamente.
Es una medida adecuada para el caso en que se desee que determinadas observaciones extremas no intervengan. Es, como vemos, el recorrido, pero teniendo solo en cuenta los valores “centrales” de la distribución.
Las expresiones que se acaban de ver miden la dispersión de la distribución en términos absolutos (vienen expresadas en las unidades de la variable, sean kilos, euros, metros cúbicos…). Por eso, se llaman medidas de dispersión absolutas. Se precisa definir, a partir de ellas, otras que hagan posible la comparación entre diferentes variables, y que tengan en cuenta el tamaño de las observaciones. Estas últimas se llamarán medidas de dispersión relativas.
Por ejemplo, si deseamos comparar los sueldos entre dos paises, no solo compararemos el salario medio (incluso refiriéndonos al salario mediana o moda). También es interesante comparar la dispersión, si existe mucha variabilidad entre los salarios, o si hay mucho recorrido (diferencias máximo salario y mínimo salario). Podríamos comparar euros con dolares realizando una conversión, obviamente, para tener las dos variables en la misma unidad de medida. Pero tampoco va a ser necesario, como veremos a continuación.
2.8.6 Coeficiente de variación
Si una variable \(X\) viene dada en metros, su desviación típica viene también dada en metros. Si quisieramos comparar su dispersión con la de una variable \(Y\) expresada en centímetros, podriamos convertir la variabble \(X\) a centímetros. Pero, si no existe manera de realizar esa conversión (supongamos una variable en metros y otra en kilogramos), no podríamos, a priori, comparar las dispersiones.
El coeficiente de variación, también llamado coeficiente de variación de Pearson (debido a su creador Karl Pearson) se define como el cociente entre la desviación típica y el valor absoluto de la media: \[ CV=\frac{S}{ \vert \bar{X} \vert }.\] Se trata de una medida adimensional (no tiene unidades), y permite comparar la dispersión de varias distribuciones. A mayor valor de \(CV,\) menor representatividad de la media aritmética, y viceversa. En general, se suele convenir en que valores de \(CV\) menores a 0.1 indican una alta concentración, entre 0.1 y 0.5 una concentración media, y valores superiores a 0.5 (o 1 según algunos libros) una alta dispersión y una media poco o nada representativa.
X=c(0.1,0.2,0.3,0.4,0.5)
Y=c(1000.1,1000.2,1000.3,1000.4,1000.5)
# ambas variables tienen la misma
# desviación típica,
sd(X);sd(Y)## [1] 0.1581## [1] 0.1581# sin embargo, los coeficientes
# de variación son muy diferentes
sd(X)/mean(X); sd(Y)/mean(Y)## [1] 0.527## [1] 0.0001581# la media de la segunda variable
# es mucho más representativa.El coeficiente de variación de Pearson es el que debe usarse para comparar la dispersión entre diferentes variables. Aquella variable con mayor coeficiente tiene mayor dispersión.
2.8.7 Simetría
Diremos que una distribución es simétrica respecto a un parámetro cuando los valores de la variable equidistantes de dicho parámetro tienen la misma frecuencia. La simetría suele referirse a la simetría respecto de la media aritmética, o respecto de la mediana.
Una distribución o variable es simétrica si, gráficamente, levantamos un eje o línea vertical sobre la media (o mediana, según el caso) y el dibujo a ambos lados de dicho eje es idéntico. Tengamos en cuenta que, si una distribución es simétrica, la media aritmética y la mediana van a coincidir.

Figura 2.38: Distribución asimétrica a la derecha.
Estudiar la simetría de una distribución es una manera de estudiar la forma de una distribución. Hemos dicho que la estadística se ocupa del estudio de poblaciones, que a su vez están compuestas de variables. La manera de estudiar las mismas es conocer sus valores medios (medidas de posición), su variabilidad (dispersión) y su forma. Dos variables (por ejemplo las estaturas de los hombres de dos naciones), cuanto más se parezcan en estos 3 conceptos, más similares serán. Como veremos en capítulos posteriores, la simetría es una propiedad que aparece en más ocasiones de lo que quizá pudiera suponerse, a priori, en muchas variables o distribuciones.
Si una distribución no es simétrica, entonces es asimétrica, y la asimetría puede presentarse:
- a la derecha (
asimetría positiva: cola de la distribución más larga a la derecha) - a la izquierda (
asimetría negativa: cola de la distribución más larga a la izquierda).
Los coeficientes de simetría son valores numéricos que indican si la distribución es simétrica y, caso de no serlo, la tendencia o signo de su asimetría. Uno de los coeficientes de simetría más utilizados es el llamado primer coeficiente de Fisher: \[g_{1}=\frac{m_{3}}{S^{3}}\]
siendo \(m_{3}\) el momento respecto a la media de orden 3, es decir
\[m_{3}=\frac{1}{n} \sum _{i=1}^{n}
\left( x_{i}-\overline{x}\right) ^{3}\] y \(S\) la desviación típica. Como vemos, es una medida adimensional (tanto en el numerador como en el denominador las unidades de la variable aparecen elevadas al cubo, por lo que al efectuar la división no hay unidades), y esto nos permite comparar simetrías de distintas variables.
Si una distribución es simétrica, \(g_{1}=0.\)
Si \(g_{1}<0\) entonces la distribución es asimétrica negativa.
Si \(g_{1}>0\) entonces es asimétrica positiva.
Cuando la distribución es simétrica, coinciden la media y la mediana.
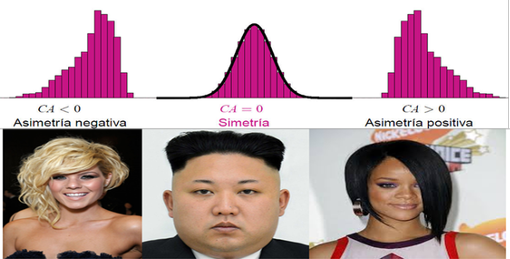
Figura 2.39: Pelo y Simetria.
Al igual que ocurría con la varianza, la fórmula del coeficiente de asimetría puede variar, por mótivos técnicos, dependiendo del programa estadístico que se utilice. Conviene siempre mirar el manual para tener clara la fórmula. En todo caso, los valores deben ser parecidos, y lo importante es el signo (positivo para asimetría a la derecha y negativo al contrario), que no debe depender del programa utilizado. Esto debe servir como regla para cualquier otro coeficiente de simetría que encontremos (en un libro, en google o en una papelera de algún matemático loco): el coeficiente de simetría positivo denotará asimetría a la derecha. Coeficiente negativo, asimetría a la izquierda. Un coeficiente cero (en realidad, próximo a cero puesto que la realidad muchas veces es más tozuda que la teoría) implicará simetría.
# estatura en centimetros
x=Datos$estatura * 0.254
x=na.omit(x)
plot(density(x), "Estatura hombres raza blanca")Figura 2.40: Estimación de la densidad de la variable estatura.
# peso en kg
x=Datos$peso * 0.0453
x=na.omit(x)
plot(density(x), "Peso hombres raza blanca")Figura 2.41: Estimación de la densidad de la variable peso.
Distinguimos claramente la asimetría del Peso frente a la simetría de la Estatura. La distribución del Peso es asimétrica a la derecha. Tengamos en cuenta que la altura es una variable antropométrica que no es susceptible de ser modificada como el peso (porque los bollitos de pan con chocolate están muy buenos, pero no aumentan la estatura).
2.8.8 Curtosis
Otra manera de estudiar la forma de una distribución es mediante la concentración existente en su “zona central” (alrededor de la media o mediana, esto es, considerando distribuciones simétricas o próximas a la simetría). La mayor o menor concentración de frecuencias alrededor de la media, en este caso, dará lugar a una distribución más o menos apuntada. El grado de apuntamiento de una distribución se calcula a través del coeficiente de apuntamiento o de curtosis, para lo cual se compara con la llamada distribución Normal o Gaussiana.
Supongamos una variable \(X\) cuya media es \(\overline{x}\) y su desviación típica es \(\sigma_x\). La siguiente función matemática (Figura 2.42) recibe el nombre de función gaussiana (en honor a Karl Gauss): que, obviamente, es una función harto rara, pero que su dibujo es el de una campana, con eje de simetría en el valor medio \(\overline{x}\)
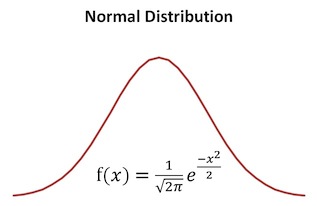
Figura 2.42: Curva Normal o Campana de Gauss.
Para estudiar el apuntamiento de una variable se puede dibujar el histograma de la misma, junto con la función 2.42. Por ejemplo, consideremos los datos de peso considerados hace un momento
# pasamos a kg
x=Datos$peso * 0.0453
x=na.omit(x)
# calculamos la media y desviación típica
media=mean(x)
des = sd(x)
#dibujamos el histograma
hist(x, probability = TRUE)
# ordenamos los datos x
x0=sort(x)
# calculamos la función f en los puntos x0
y0=dnorm(x0, mean=media, sd=des)
# dibujamos la función f
lines(x0,y0, col="red") Ante todo, observamos que la comparación del apuntamiento, de manera visual, no va a ser perfecta. El apuntamiento se fija en la concentración alrededor de la zona central. Como ya habíamos visto, la variable peso no es simétrica. Cuando dibujamos la función de densidad 2.42 utilizando la media y la desviación típica calculada a partir de los datos, vemos que la correspondiente campana de Gauss está “desplazada” con respecto al histograma de la distribución.
Quizá esta comparación sea más clara si realizamos una estimación de la función de densidad de los datos de la misma variable peso.
# pasamos a kg
x=Datos$peso * 0.0453
x=na.omit(x)
media=mean(x); des=sd(x)
# dibujamos la estimación de la
# función de densidad del peso
plot(density(x))
# ordenamos los datos x
x0=sort(x)
# calculamos la función f en los puntos x0
y0=dnorm(x0, mean=media, sd=des)
# dibujamos la función f
lines(x0,y0, col="red") De cualquier modo, a simple vista, diríamos que esta variable tiene mayor apuntamiento o curtosis que la distribución normal, que es la que se establece de referencia. Así, se dice que la distribución es:
mesocúrtica (o que la variable tiene el mismo apuntamiento que la normal),
platicúrtica (la variable es menos apuntada que la normal)
leptocúrtica (la variable es más apuntada que la normal).
En el caso anterior, la variable peso sería leptocúrtica.
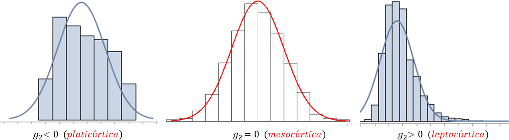
Figura 2.43: Distribuciones según la curtosis.
De todas formas, al igual que en el caso de la simetría, es posible definir coeficientese numéricos para medir la curtosis. El llamado coeficiente de curtosis (o también segundo coeficiente de Fisher) toma la expresión \[ g_2=\dfrac{m_4}{s^4} -3,\] siendo \(s\) la desviación típica y \[m_4=\dfrac{1}{n}\sum_{i=1}^n \left(x_i-\overline{x}\right)^4.\]
Como vemos, este coeficiente \(g_2\) es adimensional, con lo cual sirve para comparar la curtosis de diferentes variables. Cuando dicho coeficiente vale \(0\), coincide con el de la campana de Gauss,
Básicamente, el cálculo de la curtosis de una variable se utiliza para establecer una comparación con la variable normal que tenga la misma media y desviación típica. El objetivo es analizar si podemos considerar que la variable en estudio es “aproximadamente normal” Repetimos que la curtosis sólo tiene interés medirla en distribuciones simétricas o ligeramente asimétricas, que “puedan parecerse” a la curva Normal o campana de Gauss.
Nota histórica: la palabra KURTOSIS fue utilizada por primera vez por Karl Pearson en (Pearson 1905). Este término está basado en el griego kyrtos o kurtos (curvado o arqueado).
Pearson introdujo los términos leptocúrtico, platicúrtico y mesocúrtico, escribiendo en
(Pearl 1905): “Given two frequency distributions which have the same variability as measured by the standard deviation, they may be relatively more or less flat-topped than the normal curve. If more flat-topped I term them platykurtic, if less flat-topped leptokurtic, and if equally flat-topped mesokurtic”.
Desde un punto de vista físico, hemos visto que:
la media aritmética representa el centro de gravedad.
la varianza representa el momento de inercia.
La curtosis podría entenderse como una especie de “varianza de la varianza”. La curtosis viene a ser una medida de la dispersión de la variable, pero alrededor de los valores media - desviación típica y media + desviación típica.
Los Valores altos para la curtosis se dan en 2 circunstancias: cuando la masa de probabilidad se concentra alrededor de la media, o cuando la masa de probabilidad se concentra en las colas.
La definición de Pearson se utiliza en física, como un indicador de intermitencias en turbulencias.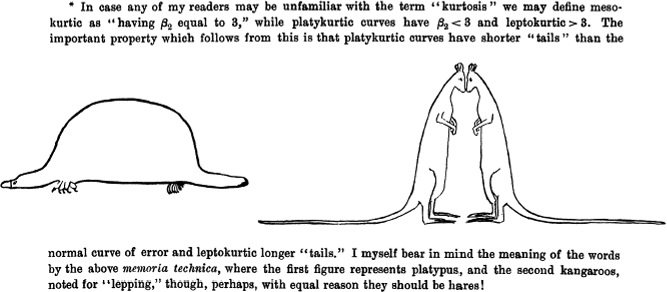
Figura 2.44: Dibujo original hecho por Student (Gosset) para acordarse de los valores de la curtosis.
2.8.9 Tipificación de una variable
Dada una variable \(X\) con media \(\overline{X}\) y desviación típica \(S_X\), la tipificación consiste en realizar la siguiente transformación:
\[ Z=\frac{X-\overline{X}}{S_X}\]
A la nueva variable \(Z\) se le llama variable estandarizada o tipificada, y tiene media 0 y desviación típica 1.
Aunque un ejemplo no demuestra nada, es más fácil de entender:
# consideramos un conjunto cualquiera de datos
X= c(3,8,1,1.1, -3.5, -6, 15)
#calculamos su media y desviación típica
media=mean(X)
des = sd(X)
# creamos una nueva variable donde a cada dato
# le restamos la media y dividimos
# por la desviación típica
Z= (X-media)/des
# calculamos la media y desviación típica de Z
mean(Z) ## [1] 5.85e-17sd(Z) ## [1] 1Restar la media a cada dato \(x_i\) es trasladar los datos, centrarlos, puesto que ahora el centro de los datos es cero.
Dividir por la desviación típica es hacer un cambio de escala. Ahora la escala va a ser una unidad.
Los valores tipificados se convierten en datos adimensionales, centrados en el cero y escala uno. Por todo lo anterior, la tipificación tiene la propiedad de hacer comparables valores individuales que pertenecen a distintas distribuciones, aún en el caso de que éstas vinieran expresadas en diferentes unidades.
Izán se ha ido de Erasmus a Andorra, donde ha obtenido una nota de 25 en estadística, mientras que Yonathan ha estudiado en Corea del Norte, obteniendo una nota de 740. Para poder comparar las notas de Izán y de Yonathan, hay que saber que las notas de la clase de Izán tienen media de 20 y desviación típica de 4, mientras que en Corea del Norte la nota media es de 666 con desviación típica de 66.
Así, las puntuaciones tipificadas fueron \(\frac{25-20}{4}=1.25\) y \(\frac{740-666}{66}=1.12\)
Una vez estandarizadas, observamos que la nota de Izan es superior a la de Yonathan.
Esta operación es la única forma que se tiene de comparar valores individuales de dos medidas diferentes. Estandarizar es una palabra muy utilizada, que significa “ajustar a un estándar” o patrón de uso común. Si hablamos de que un determinado sitio “queda muy lejos”, obviamente no sería lo mismo si nos referimos a llegar a dicho sitio en coche que andando. Para poder realizar una comparación habrá siempre que tener algún valor de referencia que nos permita realizar esa comparación. Es algo equivalente a cuando realizamos un porcentaje. Si decimos que el precio de un producto ha subido el 20 por ciento, frente al precio de otro que ha subido sólo un 3 por ciento, entendemos la diferencia, aún cuando estemos hablando de productos muy distintos entre sí.
2.8.10 Tamaño del efecto
El llamado tamaño del efecto (effect size) en una prueba estadística corresponde a una magnitud estandarizada. Si, por ejemplo, se afirma que un tratamiento disminuye el peso en 10, no sería lo mismo decir 10 kilos que 10 libras, y lo lógico sería indicar un 10 por ciento. Si se desean comparar dos tratamientos, la forma más clara de hacerlo sería a traves de puntuaciones estandarizadas (como en el ejemplo que hemos puesto arriba: si comparamos dos técnicas de estudio, una podría mejorar el rendimiento más que otra, y lo lógico es indicar cual tiene un “tamaño” mayor).
2.8.11 Diagrama de caja (Box-Plot)
Se trata de una representaciones gráfica sencilla que no necesita un número elevado de valores para su construcción. Sirve para visualizar tanto la dispersión como la forma de una variable. Asimismo, es especialmente útil para comparar diferentes distribuciones de manera simultanea.
Como dice su nombre, consta de una caja, donde la misma representa el cincuenta por ciento central de la distribución (va de \(Q_{1}\) o primer cuartil a \(Q_{3}\) o tercer cuartil), y la línea situada en el interior de la caja es la mediana.
En este gráfico, \(Q_{1}\) recibe el nombre de bisagra inferior y \(Q_{3}\) bisagra superior. Los extremos inferiores y superiores de los segmentos (también llamados bigotes) delimitan lo que se denomina como valores normales y coinciden, respectivamente, con el mínimo y el máximo de los valores una vez excluidos los candidatos a valores anómalos. Los candidatos a valores anómalos se etiquetan como atípicos y coinciden con aquellas observaciones que se encuentran fuera del intervalo \(\left( LI,LS \right)\), donde:
\[ LI=Q_{1}-1.5R_{I}, \ \ \ LS=Q_{3}+1.5R_{I},\]
es decir, a una distancia de \(Q_{1}\), por la izquierda, o de \(Q_{3}\), por la derecha, superior a una vez y media el recorrido intercuartílico (\(R_{I}=Q_{3}-Q_{1})\). En este caso se llaman atípicos de primer nivel. Cuando la distancia, por uno de los dos lados, es superior a tres recorridos intercuartílicos, el valor atípico se denomina de segundo nivel, o dato extremo.
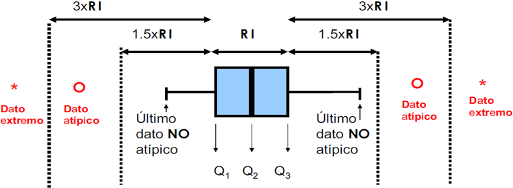
Figura 2.45: Características de un Boxplot.
Los valores atípicos de primer y segundo nivel quedan normalmente identificados en el diagrama de cajas por símbolos diferenciados, debiendo considerarse la revisión de los mismos (pueden corresponder a mediciones mal efectuadas), puesto que podrían corresponder a mediciones mal efectuadas, o a datos no pertenecientes a la variable que se está observando.
El diagrama de cajas revela rápidamente la simetría o asimetría de la distribución, pues será asimétrica a la derecha si desde la mediana la caja y los bigotes son más largos a la derecha que a la izquierda (será asimétrica a la izquierda si ocurre lo contrario).
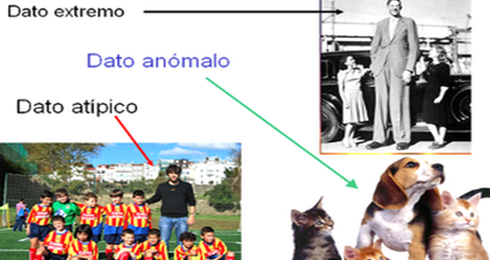
Figura 2.46: Datos atípicos, extremos y anómalos.
el diagrama de tallo y hojas, Tukey adquirió pronto fama de genio. El gráfico de caja y bigotes fue bautizado así, por lo visto, porque las lineas que sobresalen de la caja hacia los lados le recordaron los bigotes de un gato (recordemos que “whisker” significa bigotes de gato). A dia de hoy, el boxplot, que es un gráfico muy sencillo de realizar y muy práctico para la comparación rápida de múltiples variables, es uno de los diagramas más utilizados en estadística. Curiosamente, el término que se generalizó fue el de boxplot; el de whisker ni siquiere aparece en muchos textos.
John Tukey fue también famoso por su cordialidad y frases ocurrentes. En la siguiente imagen aparece una de las más conocidas:

Figura 2.47: El inefable John Tukey.
Edad que tenía un actor/actriz al recibir el Oscar al mejor actor/actriz (datos actualizados hasta 2017).
Tenemos 4 variables con edades (oscar a mejor actor/actriz principal/secundario). Para los oscars a mejor actriz y mejor actor principal tenemos 89 datos (un dato por año desde 1929 hasta 2017). Los oscar a mejor actor o actriz de reparto comenzaron a darse varios años más tarde.
Primero hacemos un sumario de las medidas estadísticas básicas:
premios_oscar <- read_excel("Data/premios-oscar.xlsx")
#cargamos los datos y los preparamos
X<- (premios_oscar$actor_principal)
Y<- (premios_oscar$actriz_principal)
Z<- (premios_oscar$actor_secundario)
W<- (premios_oscar$actriz_secundaria)
pander(summary(X))| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 29 | 38 | 42 | 44.07 | 49 | 76 |
pander(summary(Y))| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 21 | 28 | 33 | 36.03 | 41 | 80 |
pander(summary(Z))| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. | NA’s |
|---|---|---|---|---|---|---|
| 21 | 41 | 47 | 50.68 | 60 | 83 | 8 |
pander(summary(W))| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. | NA’s |
|---|---|---|---|---|---|---|
| 11 | 31 | 39 | 40.69 | 47 | 78 | 8 |
y, a continuación, un boxplot de las 4 variables (Figura 2.48).
boxplot(X,Y,Z,W) Figura 2.48: Boxplot básico
Si queremos hacer un boxplot bastante “profesional”, podemos usar la libreria plotly, que, básicamente, nos permite crear un gráfico interactivo y que permite hacer zoom, mediante la instrucción plotly(g) donde g es un gráfico que podemos crear mediante la librería ggplot2. De todas formas, está claro que la interactividad solo se puede ver en el formato de página web de este libro. Además, tengase en cuenta que utiliza bastante memoria.
fac<-c(rep("actor_principal",length(X)),
rep("actriz_principal",length(Y)),
rep("actor_secundario",length(Z)),
rep("actriz_secundaria",length(W)))
# vector con todas las edades
edad<-c(X,Y,Z,W)
# creamos una estructura
# de dos vectores, edad y
# tipo (actor principal, actriz principal...)
dt<-data.frame(edad,fac)
tipo_act<-c(rep("actor_principal",length(X)),
rep("actriz_principal",length(Y)),
rep("actor_secundario",length(Z)),
rep("actriz_secundaria",length(W)))
edad<-c(X,Y,Z,W)
dt<-data.frame(edad,tipo_act)
library(plotly)
library(ggplot2)
p <- ggplot()+
geom_boxplot(data=dt,
aes(x=tipo_act, y=edad, color=tipo_act))+
ggtitle("Edad de ganadores de oscar")+
labs(y="Edad")
ggplotly(p) Vemos que, para la variable Edad que tenía el actor que ganó el oscar al mejor actor principal la caja se mueve entre los 38 y los 50 años. La mediana es 42 años. La edad media está alrededor de los 44 años (aunque este valor no aparece en el diagrama).
Las edades varían desde un mínimo de 29 años (Adrien Brody en “El pianista” en el 2002) y un máximo de 76 años (Henry Fonda en 1982). Con respecto a las mujeres que ganaron el Oscar a la mejor actriz principal, la caja del gráfico correspondiente (el tercero, de color azul) nos indica que el 50 por ciento central de las edades es bastante menor. Esto quiere decir que las mujeres ganadoras del oscar, por lo general, lo ganan siendo más jovenes (comparadas con los hombres). La mediana de las edades es 33 y la media aritmética ronda los 36 años. Si bien los extremos son 21 años (Marlee Matlin en 1987) y 80 (Jessica Tandy en 1990), vemos que en esta segunda variable hay unos cuantos valores atípicos (esos puntos aislados que se separan de la linea del gráfico), que significa que están alejados de la tónica general de los datos.
Así, de un solo vistazo, podemos comparar estas dos variables y también las correspondientes a las edades de ganadores de oscar a mejor actor y actriz secundario/a, donde comprobamos que la tendencia de mayor edad (en general) en los hombres frente a las mujeres se mantiene.
El diagrama de cajas es muy útil también para estudiar la asimetría de una variable y poder comparar entre varias. En este ejemplo, vemos que la distribución que parece más simétrica es la correspondiente a las edades de los actores secundarios (la longitud desde la mediana hacia abajo y hacia arriba son similares). Mientras tanto, las otras tres variables presentan asimetría positiva (son más largas desde la mediana hacia la derecha).
Presentamos ahora en dos gráficos la estimación de la densidad de las variables edad actor/actriz principal y edad actor/actriz secundario. Estas gráficas nos permiten comparar la distribución de las edades con mucha claridad.
Cuanto más alta es la densidad en un cierto rango de edad, significa que hay más datos en el mismo. Observamos que, en ambos casos, las edades de las mujeres van “retrasadas” con respecto a los hombres, es decir, que los hombres tienden a ganar el Oscar con mayor edad que las mujeres. Estos resultados pueden servir para corroborar que los papeles más interesantes para las mujeres (y que les permiten ser nominadas y por tanto ganar un Oscar) se le ofrecen a las mujeres más jovenes, mientras que en los hombres parece que existen papeles atractivos en todas las edades.
Curiosidad cinéfila: Oscar en 1992 a Jack Palance, que en aquel momento tenía 72 años. Atención al minuto 1:20.
Estudiemos ahora la situación en España
Aquí no tenemos Oscar, tenemos los Goya, pero desde hace menos tiempo. En concreto, desde 1986. Vamos a realizar exactamente el mismo análisis de antes. El gráfico de box-plot es
# Leemos los datos directamente de excel
# con la libreria readxl
library(readxl)
premios_goya <- read_excel("Data/premios-goya.xlsx")
#cargamos los datos y los preparamos
X<-na.omit(premios_goya$edad_actor_principal)
Y<-na.omit(premios_goya$edad_actriz_principal)
Z<-na.omit(premios_goya$edad_actor_reparto)
W<-na.omit(premios_goya$edad_actriz_reparto)
tipo_act<-c(rep("actor_principal",length(X)),
rep("actriz_principal",length(Y)),
rep("actor_secundario",length(Z)),
rep("actriz_secundaria",length(W)))
edad<-c(X,Y,Z,W)
dt<-data.frame(edad,tipo_act)
library(plotly)
library(ggplot2)
p <- ggplot()+geom_boxplot(data=dt,
aes(x=tipo_act, y=edad, color=tipo_act))+
ggtitle("Edad de ganadores de Goya")+
labs(y="Edad")
ggplotly(p) Fijémonos que la diferencia de gráficos es acusada entre actores y actrices cuando nos fijamos en el premio a actriz/actor principal, pero no en cambio al comparar edades en premios a actor/actriz de reparto. En el caso de las edades de las actrices que ganaron el Goya a la mejor actriz principal, ya aparecen como puntos atípicos (aislados del resto) una actriz de 61 años (Amparo Rivelles, que ganó en la primera ceremonia de los Goya), y Rafaela Aparicio que tenía 83 años cuando lo ganó.
Las gráficas corroboran la impresión del diagrama de cajas. Las distribuciones son muy parecidas en el caso de las edades de los premios secundarios, pero muy diferente en el caso de los premios a papeles principales (resaltemos como hay mucha concentración de datos en el rango de 20 a 40 años).
La diferencia de nuestro cine con el de Hollywood se centra, como vemos, en lo que respecto a los papeles no principales. Sin embargo, con respecto a los papeles principales, las actrices españoles se quejan de igual forma de que no existen tantos buenos papeles principales para actrices “maduras”, como sí existen para sus compañeros masculinos.
Y como no podíamos terminar este análisis sin alguna fotografía de cine, pues recordar que estos dos actores tienen cada uno un Oscar y un Goya (en realidad más de uno), y además son pareja. ¿Cuál es la probabilidad de darse semejante coincidencia?
References
Balanda, Kevin P, and HL MacGillivray. 1988. “Kurtosis: A Critical Review.” The American Statistician 42 (2). Taylor & Francis Group: 111–19.
Desrosières, Alain. 2004. “La Política de Los Grandes Números.” Historia de La Razón Estadística. Barcelona: Melusina.
Hacking, Ian, and Alberto L Bixio. 1995. La Domesticación Del Azar: La Erosión Del Determinismo Y El Nacimiento de Las Ciencias Del Caos. Gedisa Editorial.
Pearl, Raymond. 1905. “Biometrical Studies on Man: I. Variation and Correlation in Brain-Weight.” Biometrika 4 (1/2). JSTOR: 13–104.
Pearson, Karl. 1905. “DAS Fehlergesetz Und Seine Verallgemeiner-Ungen Durch Fechner Und Pearson. a Rejoinder.” Biometrika 4 (1-2). Oxford University Press: 169–212.
Perrot, Jean-Claude. 1992. “Une Histoire Intellectuelle de L’économie Politique(XVIIe-Xviiie Siècle).” Civilisations et Sociétés. Ehess.
Tukey, John W. 1977. Exploratory Data Analysis. Vol. 2. Reading, Mass.
Wickham, Hadley. 2016. Ggplot2: Elegant Graphics for Data Analysis. Springer.