2.7 Variables continuas

Analicemos ahora el caso de variables continuas. En general, el análisis para variables continuas coincide con el análisis para variables discretas cuando existen muchas observaciones, la mayoría de ellas distintas. Por ejemplo, la variable edad (en años) se consideraría, en principio, una variable discreta, puesto que no se utilizan valores decimales (tipo \(1.5\) para año y medio, etc.). Si disponemos, supongamos, de datos de edad correspondientes a muchas personas, lo más probable será que tengamos muchos valores diferentes. Realizar un diagrama de barras o uno de sectores puede no ser una buena idea, ya que ofrecerían poca información.

En este supuesto (variables continuas, o, en general, variables con muchos valores diferentes), los datos pueden disponerse agrupándolos o clasificándolos en intervalos, e indicando el número de observaciones que caen dentro de cada intervalo.

Para ello se elige un número \(a_0 \leq min(X)\), y otro \(a_k \geq max(X)\), y se divide el intervalo \([a_0,a_k]\) en \(k\) intervalos.

Figura 2.10: Clasificación de datos en intervalos.

Supongamos que tenemos los siguientes datos de una variable \(X\): \[2,3,4,4.5,4.5,5.6,5.7,5.8,6,6.1,6.5,7,7,7,\] \[7.5,7.5,7.5,8.3,9,10.2,10.4,11,11.1,11.5,12,13\]

Una posible representación o clasificación en intervalos es la siguiente:

X=c(2,3,4,4.5,4.5,5.6,5.7,5.8,6,6.1,6.5,7,7,
    7,7.5,7.5,7.5,8.3,9,10.2,10.4,11,11.1,11.5,12,13)
div<-table(cut(X,breaks=7))
library(pander)
mat <- data.frame(div)
names(mat) <- c("Intervalos", "Frecuencias ($n_i$)" )
x<- xtable(mat)
pander(x)

Intervalos	Frecuencias (\(n_i\))
(1.99,3.57]	2
(3.57,5.14]	3
(5.14,6.71]	6
(6.71,8.29]	6
(8.29,9.86]	2
(9.86,11.4]	4
(11.4,13]	3

Esta clasificación nos dice el número de datos que hay en cada intervalo. El indicar los intervalos de la forma \((a,b]\) indica que el dato \(a\) no se cuenta en este intervalo, y sí se cuenta el dato \(b\).

Datos de la variable Edad de los pasajeros del Titanic. Supongamos, inicialmente, dado que es una variable discreta, que realizamos un diagrama de barras o un diagrama de sectores.

x=Datos_Titanic$edad
# clasificamos los datos
y=table(x)  
# 2 gráficos en  1 fila, 2 columnas 
op <- par(mfrow = c(1,2))  
barplot(y)
pie(y)

# dejamos los gráficos en formato 1 x 1
par(op)  

Como vemos, el gráfico de barras no es util porque se “agolpa” la información, y el gráfico de sectores menos. Por este tipo de cosas, es más conveniente clasificar los datos, considerándolos como datos procedentes de una variable continua.

Para clasificar los datos en, por ejemplo, seis intervalos, hacemos:

X=Datos_Titanic$edad
table(cut(x, breaks=6))

(0.0869,13.5]	(13.5,26.8]	(26.8,40.1]	(40.1,53.4]	(53.4,66.7]	(66.7,80.1]
99	375	345	150	68	9

La forma general de una tabla de frecuencias es la siguiente:

Intervalo (o dato)	Frecuencia absoluta	Frecuencia relativa
\(x_{i} \ o \ [a_0,a_1)\)	\(n_{i}\)	\(f_{i}\)
\(x_{1}\)	\(n_{1}\)	\(f_{1}= n_{1}/{n}\)
\(x_{2}\)	\(n_{2}\)	\(f_{2}= n_{2}/{n}\)
\(\vdots\)	\(\vdots\)	\(\vdots\)
\(x_{r}\)	\(n_{r}\)	\(f_{r}= n_{r}/{n}\)

2.7.1 Histograma de Frecuencias.

Es uno de los gráficos más antiguos (y de los más utilizados) para representar una variable continua. Una vez que se tienen los intervalos, sobre cada uno de ellos se levanta un rectángulo de área o altura la frecuencia (absoluta o relativa), de manera totalmente equivalente al diagrama de barras: cada intervalo es como un valor de una variable discreta. Cuantos más datos haya en un intervalo, este será más alto, y cuantos menos datos, más bajo.

Su inventor fue Karl Pearson, y el nombre viene de su primera utilización para representar datos históricos.

Histograma de la variable Edad de los datos del Titanic, realizada por medio de los gráficos básicos de R.

x=Datos_Titanic$edad
hist(x, main="Histograma de la edad de los pasajeros del Titanic", xlab="Años")

Figura 2.11: Histograma de la variable Edad

Como comprobamos, con el comando histno es necesario decirle nada sobre la clasificación de datos de la variable; lo hace automáticamente.

Histograma de la variable Magnitud correspondiente a los terremotos registrados en Galicia por el Instituto Geográfico Nacional (IGN) hasta mayo de 2008, y Salarios en España en 2012. Figura 2.12:

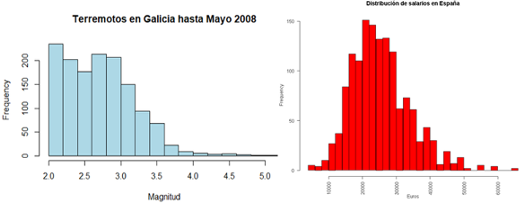
Figura 2.12: Izquierda: magnitudes de terremotos en Galicia. Fuente: IGN. Derecha: salarios brutos anuales de asalariados en 2012. Fuente: Ministerio.

2.7.1.1 El número de intervalos.

El histograma nos sirve para ver el comportamiento de los datos, desde el mínimo al máximo, advirtiendo donde se concentran más datos y donde menos. El aspecto de un histograma (y por tanto el de la distribución de los datos) puede cambiar mucho dependiendo del número de intervalos que se utilice. Los programas estadísticos suelen utilizar alguna fórmula que depende del número \(n\) de datos. Por ejemplo, por defecto, el software R o el SPSS utilizan la llamada fórmula de Sturges, que considera el número de intervalos como \(log_2 (n).\) Otros paquetes utilizan \(\sqrt{n}\). La selección de un número u otro es un problema matemático con relativa complejidad.

El comando básico hist de R puede calcular el número de intervalos mediante otros métodos alternativos al de Sturges, como es del de Scott o el de Friedman-Diaconis (FD) (ver (Wand 1997) para un estudio sobre la selección del número óptimo de intervalos).

Observemos como cambia la forma o aspecto de un histograma según el número de intervalos. En el comando básico de R hist esto se controla escribiendo breaks=, en donde breaks es el número de intervalos.

Vamos a considerar un ejemplo con el fichero de datos que corresponde a algunas variables de la encuesta nacional de salud en Estados Unidos durantes los años 1959 a 1962 (NHES1) (Se puede acceder a estos datos y otros del libro mediante el enlace que está en la página principal). En este fichero se dispone del peso y estatura de 6673 hombres y mujeres (raza blanca y negra). Con los datos del peso de los hombres de raza blanca realizamos 4 histogramas con distintos intervalos cada uno (Figura 2.13), para ver como se producen diferencias en el dibujo y, por lo tanto, en la forma de la distribución.

 NHANES1 <- read.csv("Data/du1003.csv", header=TRUE, sep=";")
 library(dplyr)
 # filtramos para quedarnos con hombres de raza blanca (código 1)
 Datos=NHANES1 %>%
 filter(v==1) 
 
# VARIABLE ESTATURA
#  
x=Datos$peso   
 
# ponemos gráficos en formato 2 x 2
op <- par(mfrow = c(2, 2)) 
# número de intervalos según la fórmula de Sturges
hist(x, breaks="Sturges")  
# número de intervalos igual a 5
hist(x, breaks=5)          
 hist(x, breaks=2) 
 hist(x, breaks=60)

Figura 2.13: Histogramas variando el número de intervalos.

# vuelve a poner gráficos de 1 en 1
par(op)                 

Si se quiere probar, de forma interactiva, como cambia un gráfico de histograma según se cambia el número de intervalos (o el ancho de los mismos) se puede probar, dentro de Rstudio, el siguiente trozo de código:

library(manipulate)
x=Datos_Titanic$edad
manipulate( hist(x, breaks=c, density = 25), c=slider(1,11) )  

Mostramos una gráfica generada por el método anterior (Figura 2.14):

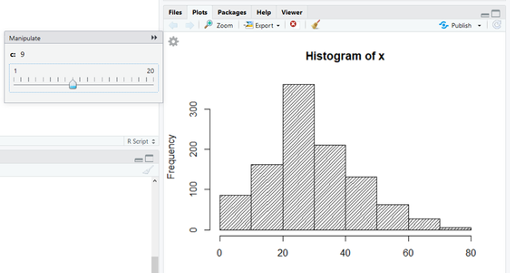
Figura 2.14: Captura de pantalla de histograma.

Para probar que, usando otras librerias (o paquetes) se pueden conseguir gráficos con mayor número de prestaciones, ponemos otro ejemplo de gráfico interactivo; en este caso utilizando la libreria ggvis. Copiando el trozo de código que viene a continuacion (hay que instalar primero la libreria) obtendremos otra forma de generar histogramas donde podemos variar a mano el número de intervalos.

# generamos datos simulados
x1=rnorm(1000,0,3)  
# llamamos a la librería ggvis
library(ggvis)      
datox=data.frame(x1)  
datox %>%   
 ggvis(~x1,   
      fill :="salmon"  
        )%>%  
layer_histograms(width =  input_slider(0.1, 2))%>%  
add_axis("x",title="Histograma de la variable ")%>% 
add_axis("y",title="")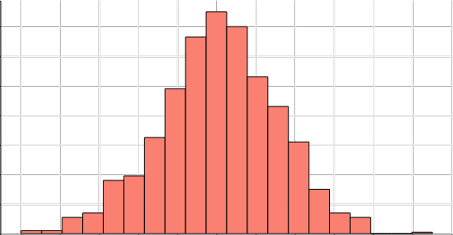  

Figura 2.15: Un gráfico generado mediante ggvis.

2.7.1.2 Polígono de frecuencias

Consiste en unir los puntos medios de los rectángulos superiores en un histograma. El polígono (Figura 2.16) parte del eje X y regresa al eje X, simplemente marcando como origen y final una distancia de los extremos igual a la longitud de un intervalo dividida entre 2

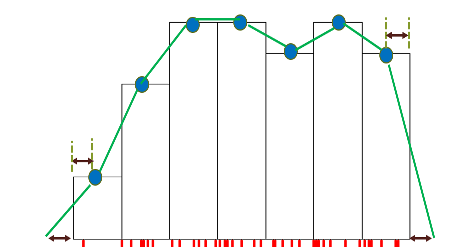
Figura 2.16: Construcción de un polígono de frecuencias.

El área encerrada entre el histograma y el eje horizontal sera \(n\), número total de datos (simplemente sumamos el área de todos los rectángulos). Si en vez de utilizar la frecuencia absoluta usamos la relativa, el área de cada rectángulo será el porcentaje de datos que hay en el mismo. El área encerrada entonces por todo el histograma y el eje horizontal será igual a 1 (es el cien por cien de los datos). Análogamente, puede comprobarse que el área encerrada entre el polígono de frecuencias y el eje horizontal también vale 1 (sólo hay que pensar que, en el polígono de frecuencias, a cada rectángulo le restamos y sumamos el área de dos triángulos, que se van compensando a lo largo de la figura).

Cargando la libreria UsingR se dibuja un polígono de frecuencias sobre un histograma con la orden simple.freqpoly() (Figura 2.17).

# library(UsingR)
x=Datos_Titanic$edad
simple.freqpoly(x)

Figura 2.17: Polígono e Histograma de la variable Edad.

2.7.2 Estimación tipo núcleo de la función de densidad

El histograma y el polígono de frecuencias no dejan de ser más que estimaciones de la función de densidad de una variable aleatoria continua. Los conceptos de variable aleatoria y de función de densidad (capítulo 5) se definen a partir de la noción de probabilidad. Como una mera aproximación, diremos que la función de densidad sería el polígono de frecuencias que se construiría si dispusiésemos de un conjunto infinito de datos. En este caso, el polígono tendría la forma de una función matemática continua y derivable (no estaría formada por uniones de segmentos).

Matemáticamente, a partir de un conjunto de datos \(x_{1},...,x_{n},\) un estimador no paramétrico tipo núcleo de la función de densidad \(f,\) evaluado en un punto cualquiera (no tiene por qué ser un dato) \(x_0\) es el definido como (Parzen 1962), \[\begin{equation} \hat{f}_{h}(x_0)=\dfrac{1}{nh}\sum_{i=1}^{n}K\left( \dfrac{x_0-x_{i}}{h}% \right) . \end{equation}\]

\(K\) es una función (llamada núcleo o kernel) continua y derivable, y \(h\) es un parámetro llamado ventana (bandwidth), que ejerce un papel equivalente al del ancho de los intervalos en el histograma (o, equivalentemente, el número de intervalos).

Veamos con un gráfico cómo funciona el estimador núcleo de la densidad. Para ello supongamos que tenemos un conjunto de 6 datos, los que aparecen representados en la gráfica 2.18:

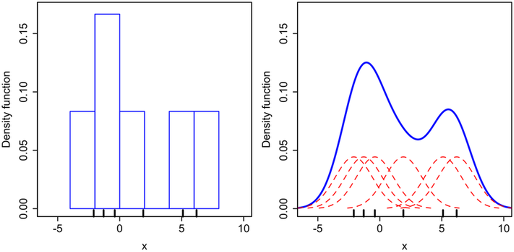
Figura 2.18: Comparativa de un histograma y un estimador núcleo de la densidad.

Hemos visto que el histograma consiste en, una vez que los datos están clasificados en intervalos, se levanta un rectángulo proporcional al número de datos. Rectángulos más altos significa que hay más datos en ese intervalo (más bajos menos datos).

Dibujar el estimador núcleo de la densidad de unos datos \(x_{1},...,x_{n}\) es como dibujar una función. Si queremos, por ejemplo, dibujar la función \(f(x)=x^2\) entre los valores \(-5\) y \(5\), seleccionamos una serie de puntos (les llamamos \(x_0\)) entre \(-5\) y \(5\), y marcamos en el plano los puntos de coordenadas \((x_0, f(x_0))\). Luego únimos todos esos puntos y tenemos la gráfica. Cuántos más puntos \(x_0\) elijamos, mayor precisión tendra el dibujo.

La forma de dibujar el estimador núcleo de la densidad es, una vez que seleccionamos esos puntos \(x_0\), marcar los puntos de la forma \((x_0, \hat{f}_{h}(x_0))\), donde la función depende de la cantidad de datos \(x_{1},...,x_{n}\) que haya alrededor del valor \(x_0\). Cuántos más datos haya “cerca” de \(x_0\), \(\hat{f}_{h}(x_0)\) toma un valor más alto. Cuántos menos datos haya cerca de \(x_0\), \(\hat{f}_{h}(x_0)\) toma un valor más pequeño.

Fijémonos en la gráfica 2.18, donde aparece, sobre cada dato, un dibujo de una curva con forma de campana. Esa es la \(K\) que aparece en la fórmula del estimador \(\hat{f}_{h}\), y es la forma en que se tiene en cuenta cada punto que hay “cerca” de \(x_0\). Cada dato \(x_i\) cerca de \(x_0\) se pondera mediante \(K((x_0-x_i)/h\).

Ese parámetro \(h\) o “ventana” juega un papel similar al del ancho o longitud de los intervalos del histograma. Lo que ocurre es que, ahora, es como si esos intervalos se movieran: para cada valor \(x_0\) donde queremos calcular \(\hat{f}_{h}(x_0)\) “abrimos” un intervalo de longitud \(h\) centrado en \(x_0\). Cuántos más datos hay en ese intervalo, \(\hat{f}_{h}(x_0)\) es más alto, pero no es un valor directamente proporcional al número de datos de ese intervalo, sino que se ponderan en función de la distancia, mediante esa función \(K((x_0-x_i)/h)\). El formato matemático de la construcción de \(\hat{f}_{h}(x_0)\) garantiza que la curva final que se dibuja va a ser una curva continua digamos “suave”, como la que aparece en la imagen de arriba a la derecha (color azul).

La interpretación gráfica representa la “densidad” o “distribución” del conjunto de datos. Donde hay más datos la curva crece, donde hay menos datos, la curva decrece. Es muy similar al polígono de frecuencias, pero no está formado por segmentos, sino por una línea continua.

Como función \(K\) puede elegirse una función continua cumpliendo condiciones sencillas de regularidad, por ejemplo la curva “normal” o curva de Gauss, o una función polinómica (Silverman 1986).

En la Figura 2.19 vemos el estimador de la función de densidad de la variable edad de los pasajeros del Titanic, junto con el histograma, realizado mediante los comandos básicos de R.

# na.omit es para no considerar valores en blanco:
X= na.omit(Datos_Titanic$edad)  
hist(X, prob=TRUE)
lines(density(X), lty="dotted", lwd=2, col="red")

Figura 2.19: Histograma y estimador de la densidad

Igual que sucede en el histograma, la forma del estimador de la densidad varía en función del parámetro ventana \(h\) que se utilice. El efecto es el mismo que en el caso del histograma. Cuanto más pequeño es el valor de \(h\), la forma del estimador de la densidad es más variable. Cuando \(h\) toma un valor muy grande, el estimador resultante adopta una forma muy suave y homogénea, pero que tampoco reflejará la realidad de los datos.

Volvemos ahora a utilizar el fichero de datos de la encuesta nacional de salud en Estados Unidos durantes los años 1959 a 1962 (NHES1). Con los datos del peso y la estatura de los hombres de raza blanca realizamos estimaciones de la densidad, cambiando los valores del parámetro h, para ver como se producen diferencias en el dibujo (Figuras 2.20 y 2.21).

 NHANES1 <- read.csv("Data/du1003.csv", header=TRUE, sep=";")
 datatable(NHANES1, options = list(pageLength = 5))  

Figura 2.20: Estimaciones de la densidad de la variable Estatura

 # filtramos para quedarnos con hombres de raza blanca (código 1)
 Datos=NHANES1 %>%
 filter(v==1) 
# VARIABLE ESTATURA
x=Datos$estatura * 0.254  # pasamos a centimetros  
plot(density(x), "Estatura hombres raza blanca")
rug(x)  # dibujo de puntos de la variable
lines(density(x, bw = 4), col = 2)
lines(density(x, bw = 10), col = 3)
lines(density(x, bw = 20), col = 4)
lines(density(x, bw = 40), col = 5)
legend(136, 0.04,
       legend = c("h=13.3", "h=6", "h=10", "h=15", "h=20"),
       col = 1:5, lty = 1) 

Figura 2.20: Estimaciones de la densidad de la variable Estatura

# VARIABLE PESO
# pasamos a kg
x=Datos$peso * 0.0453  
x=na.omit(x)
plot(density(x), "Peso hombres raza blanca")
rug(x)
lines(density(x, bw = 10), col = 2)
lines(density(x, bw = 20), col = 3)
lines(density(x, bw = 40), col = 4)
lines(density(x, bw = 50), col = 5)
legend(120, 0.025,
       legend = c("h=23.2", "h=10", "h=20", "h=40", "h=50"),
       col = 1:5, lty = 1)

Figura 2.21: Estimaciones de la densidad de la variable Peso

Como podemos comprobar en las dos gráficas de 2.20, el valor de \(h\) influye sustancialmente en la forma que ofrece la curva sobre los datos. De manera general, el valor que el comando density de R toma automáticamente suele ser el más adecuado a los datos concretos. En el primer gráfico (estatura), los datos tienen una forma de “campana”, simétrica alrededor de la estatura media, y presentando mucha menor concentración a medida que vamos hacia valores muy bajos o muy altos (hay poca gente con estatura muy alta o estatura muy baja). En cambio, para los datos del peso, esa simetría se pierde, puesto que hay una mayor concentración de datos a la derecha (más gente con peso alto que con peso bajo). Si queremos saber el valor “óptimo” del parámetro \(h\) que nos proporciona el programa escribimos density(x)$bw, que, en este último caso, es 2.3299. Este valor óptimo se calcula mediante una fórmula matemática que suele proprocionar buenos resultados prácticos; es decir, habitualmente, con este valor y un tamaño aceptable de datos (50-100 o más datos), no hay que preocuparse en tomar otro, o en hacer gráficos alternativos con otros valores.

Igual que con el histograma, mediante la libreria ggvis puede uno divertirse haciendo gráficos, cambiando automáticamente el valor del parámetro ventana (Figura 2.22), a través del siguiente código:

library(ggvis)
library(dplyr)   
NHANES1 <- read.csv("Data/du1003.csv", header=TRUE, sep=";")
#  Datos
 datatable(NHANES1, options = list(pageLength = 5))  
 # filtramos para quedarnos con hombres de raza blanca (código 1) 
 Datos=NHANES1 %>%
   filter(v==1)  
x=Datos$peso * 0.0453  # peso en kg
x=na.omit(x) 
datox=data.frame(x)  
datox %>%   
  ggvis(~x,   
        fill :="red"  
  )%>%  
  layer_densities(adjust = input_slider(0.1, 2))%>%  
  add_axis("x",title="Densidad de la variable Peso ")%>% 
  add_axis("y",title="")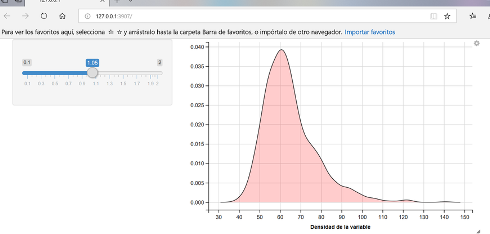  

Figura 2.22: Captura de pantalla de uno de los gráficos generados mediante la libreria ggvis.

References

Parzen, Emanuel. 1962. “On Estimation of a Probability Density Function and Mode.” The Annals of Mathematical Statistics 33 (3). JSTOR: 1065–76.

Silverman, Bernard W. 1986. Density Estimation for Statistics and Data Analysis. Vol. 26. CRC press.

Wand, MP. 1997. “Data-Based Choice of Histogram Bin Width.” The American Statistician 51 (1). Taylor & Francis: 59–64.