8.6 Contrastes de hipótesis paramétricas

8.6.1 Tipos de contrastes: bilaterales y unilaterales

Un contraste es bilateral cuando tiene la forma

$H_0: \theta=\theta_0$ (Por $\theta$ nos referimos a un parámetro teórico y por $\theta_0$ a un valor constante, un número) frente a

$H_1: \theta\neq \theta_0$

Un contraste unilateral es de la forma: $H_0: \theta=\theta_0$ frente a

$H_1: \theta=\theta_0$ o bien $H_1: \theta=\theta_0$

Con el mayor consumo de chucherías y comida basura, parece que el peso medio de los niños de 12 años ha aumentado.

Contraste unilateral:

$H_0: \mu=26 kg$ frente a $H_1:\mu > 26$

El nuevo virus zombi ha provocado una alteración en el peso de los adultos.

Contraste bilateral:

$H_0: \mu=60 kg$ frente a $H_1:\mu \neq 60$

8.6.2 Pasos a seguir al realizar un contraste de hipótesis

1.- Especificar las hipótesis nula y alternativa.

2.- Elegir un estadístico $T$ para el contraste (para medir la discrepancia entre lo observado y lo teórico). Este estadístico tendrá una función de densidad determinada que nos servirá para calcular el $p$-valor.

3.- Tomar una muestra $(x_1.x_2,...,x_n)$ y evaluar el estadístico del contraste $T(x_1.x_2,...,x_n)$.

4.- Calcular el $p-$valor

\[P(T\geq (x_1,x_2,...,x_n)/H_0),\] que viene a ser la probabilidad de obtener esos datos, si $H_0$ es cierta. Si ese valor es muy pequeño, significa que esos datos son muy improbables bajo la hipótesis nula, con lo cual tenderemos a pensar que no es cierta.

Una especie de nivel crítico es el valor 0.1, de forma que

Si el $p-$valor es más pequeño que 0.1, tenderemos a no creer en $H_0$, y, en cambio, si es más grande, tenderemos a creer en $H_0$.

En muchas ocasiones (muchos libros, artículos de investigación), se trabaja fijando un nivel de significación $\alpha$ (error de tipo I) y realizando la siguiente comparación:

Si $p< \alpha$ se rechaza $H_0$
si $p\geq \alpha$ se acepta $H_0$.

Los valores con los que se suele trabajar son $\alpha= 0.1,0.05$ o $0.01$. El más habitual es $\alpha=0.05$

Para rechazar la hipótesis nula se requiere que la probabilidad del fenómeno que se produce por casualidad sea inferior al cinco por ciento (este es el origen de la anécdota del estadístico que presenció la decapitación de 25 vacas, advirtió que una sobrevivía y desechó el fenómeno por no significativo).

Ver Problemas del nivel de significación

No rechazar una hipótesis no prueba que sea totalmente cierta. Podemos cometer un error de tipo II.

A continuación, indicamos los estadísticos que se utilizan para los principales contrastes de tipo paramétrico, y la distribución que siguen cuando la hipótesis nula es cierta.

8.6.3 Para la media de una variable normal

Supongamos que estamos trabajando con datos de una variable aleatoria $X$ que sigue una distribución normal. Supongamos que establecemos la hipótesis de que la media (teórica, que es desconocida) es igual a un cierto valor numérico:

$H_{0}:\mu =\mu _{0}.$

$\mu _{0}$ es un número concreto. Por ejemplo, se ha realizado un tratamiento a un conjunto de pacientes con dolor lumbar. A cada uno de ellos se le ha pedido que diga, en una escala de $0$ a $10$, cuánto dolor le ha reducido el tratamiento ($0$ si nada, $10$ si se ha quedado sin dolor alguno).

Suponemos que la variable $X$=reducción del dolor con el tratamiento sigue una distribución normal. Para saber si el tratamiento es efectivo, la hipótesis nula que plantearíamos es:

$H_{0}:\mu =0.$

De lo que se trata es de falsar esta hipótesis, es decir, encontrar una diferencia estadísticamente significativa entre lo que se obtenga en la muestra y lo que dice la hipótesis nula. Esta última, al considerar que la media es cero, implica que el tratamiento no tiene efectividad, puesto que, en media, no reduce el dolor.

Para realizar el contraste de hipótesis, inicialmente consideramos dos posibilidades: que conozcamos la desviación típica de la variable, o que no la conozcamos. Esta última opción es la más habitual, y la más lógica, puesto que, si no tenemos información sobre la media, es raro tenerla de la desviación típica. En el ejemplo que hemos puesto, si no se conoce la reducción media de dolor con un tratamiento (hablamos habitualmente de un tratamiento en fase experimental) pues será raro conocer su variabilidad.

En todo caso, en la mayoría de los textos realizan la distinción entre los casos de desviación típica conocida o no. Consideraremos aquí también los dos casos, igual que se hizo en el capítulo anterior de intervalos de confianza.

8.6.4 Si se conoce la desviación típica

Si tenemos una muestra $(x_1,...,x_n)$ de $n$ datos de una variable aleatoria normal, de parámetros $\mu$ y $\sigma$, la media muestral verifica \[ \bar{x} \in N\left(\mu, \dfrac{\sigma }{ \sqrt{n}}\right). \] Por lo tanto, si tipificamos la variable (restamos la media y dividimos por la desviación típica), obtenemos la variable $T$, lo que quiere decir que esta variable sigue una distribución normal estándar ($N(0,1)$).

\[ T=\frac{\bar{x}-\mu _{o}}{\sigma /\sqrt{n}}\ \ \in \ \ N(0,1) \]

Este estadistico o variable aleatoria $T$ se llama estadístico “pivote” o estadístico del contraste. Es con el que se realiza el contraste y se toma una decisión, según el valor que tome con los datos de la muestra.

El $p-$valor se calcula en función de la distribución que sigue el estadístico “pivote” del contraste, y de que el contraste sea bilateral o unilateral.

Los catedráticos de la universidad se quejan al rector de que los precios del menú del día de las cafeterías universitarias han subido expectacularmente. Para verificarlo, se envía a un vicerrector a comer a las cafeterías de las distintas facultades y se anota el precio del menú:

6, 6.6, 6.5, 5.8, 7, 6.3, 6.2, 7.2, 5.7, 6.4, 6.5, 6.2, 6, 6.5, 7.2, 7.3, 7.6, 6.8, 6

El curso anterior, el precio medio del menú era de 6.8 euros, y la desviación típica de 0.7. ¿Podrá el rector decirle a sus profesores que los precios no han subido?

Solución:

El test de hipótesis que debemos plantear es $H_0:\mu =6.8$ frente a $H_1:\mu < 6.8.$

A partir de la muestra, calculamos la media muestral, que es $\bar{x}=6.51$. El valor del estadístico es, entonces: \[ T=\frac{\bar{x}-\mu _{o}}{\sigma /\sqrt{n}} = \frac{6.51-6.8}{0.7/\sqrt{19}}=-1.8 \] Al ser un test unilateral, donde la hipótesis alternativa $H_1$ es de la forma $H_1:\ <$, el $p-$valor se calcula como el área a la izquierda de $-1.8$ (en este caso, de una variable $N(0,1)$ que es la distribución del estadístico $T$).

library(mosaic)
plotDist("norm",  groups = x >-1.8  , type="h")

pnorm(-1.8)

## [1] 0.03593

El $p-$ valor es 0.46. Si lo comparamos con el valor más utilizado para $\alpha=0.05,$ se rechazaría que la media es 6.8 y aceptaríamos que el precio medio ha bajado.

8.6.5 La prueba $t$

En la práctica, es bastante extraño conocer la desviación típica (puesto que precisamente estamos en una situación de incertidumbre de la variable. Lo habitual es no conocer ni la media ni la desviación típica). En este caso, lo que se hace es estimar la desviación típica a partir de la muestra, utilizando para ello la cuasi-desviación típica muestral $\hat{S}_{n-1}$. En este caso, el estadístico que se utiliza cambia, y también la distribución del mismo. Tenemos que usar el estimador \[ T=\frac{\bar{x}-\mu _{o}}{\hat{S}_{n-1}/\sqrt{n}}\ \ \in \ \ t_{n-1}. \] Este estimador sigue una distribución $t$ de Student, con $n-1$ grados de libertad. A este contraste de hipótesis se le llama prueba t.

Vamos a realizar el ejercicio anterior, pero suponiendo que desconocemos la desviación típica teórica de la población. En este caso, calculamos $\hat{S}_{n-1}$ con los datos de la muestra.

Recordemos que la desviación típica se calcula con sd

x=c(6,6.6,6.5,5.8,7,6.3,6.2,7.2,5.7,6.4,6.5,
    6.2,6,6.5,7.2,7.3,7.6,6.8,6)
mean(x)

## [1] 6.516

sd(x)

## [1] 0.5419

El valor del estadístico es, por lo tanto: \[ T=\frac{\bar{x}-\mu _{o}}{\hat{S}_{n-1}/\sqrt{n}}=\frac{6.51-6.8}{0.54/\sqrt{19}}= -2.3. \] Y ahora el $p-$valor lo buscamos a partir de la distribución $t$, en este caso con $19-1$ grados de libertad.

pt(-2.3, df=18)  #df son grados de libertad

## [1] 0.01681

El $p-$valor en este caso es $0.016$.

Este test puede realizarse de manera directa en R, de la forma:

x=c(6, 6.6, 6.5, 5.8, 7, 6.3, 6.2, 7.2, 5.7, 6.4, 
    6.5, 6.2, 6, 6.5, 7.2, 7.3, 7.6, 6.8, 6)
t.test(x, mu=6.8, alternative="less")

## 
##  One Sample t-test
## 
## data:  x
## t = -2.3, df = 18, p-value = 0.02
## alternative hypothesis: true mean is less than 6.8
## 95 percent confidence interval:
##   -Inf 6.731
## sample estimates:
## mean of x 
##     6.516

Supongamos, por ejemplo, que la hipótesis alternativa $H_{1}$ es de la forma $H_{1}:\mu \neq \mu _{0},$ entonces el nivel crítico o $p$-valor es $2$ veces el área a la derecha del valor absoluto del estadístico del contraste $\hat{w}$, que se calcula como qt(0.975,df=20) (recordemos que el $p$-valores es la probabilidad $P(T\geq (x_1,x_2,...,x_n)/H_0)$).

plotDist("t", df = 20, groups = x > -2.085 & x < 2.085, 
  type = "h")

Si $H_{1}$ es de la forma $H_{1}:\mu >\mu _{0},$ el $p$-valor es el área a la derecha del estadístico del contraste.

plotDist("t", df=20, groups = x > 2.085  , type="h")

Si $H_{1}$ es de la forma $H_{1}:\mu <\mu _{0},$ el $p$-valor es el área a la izquierda del estadístico del contraste.

plotDist("t", df=20, groups = x >-2.085  , type="h")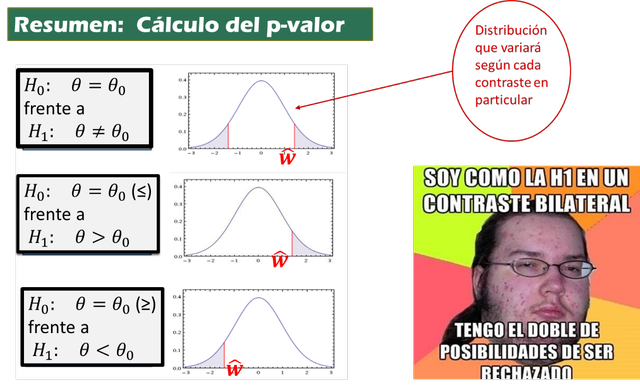

Figura 8.7: Resumen de tipos de contrastes y cálculo del $p$-valor.