6.2 El papel de Quetelet en la relevancia de la distribución normal

Figura 6.15: Adolphe Quetelet.
Adolphe Quetelet nació el 2 de febrero de 1796 en la ciudad belga de Gante. Su padre murió cuando él tenía siete años. Obligado a buscarse el sustento, Quetelet empezó a enseñar matemáticas a los diecisiete años. También compuso poesía, escribió el libreto de una ópera, fue coautor de dos obras de teatro y tradujo diversas obras literarias. Sin embargo, su tema favorito siempre fueron las matemáticas, y fue la primera persona que obtuvo el grado de Doctor en Ciencias por la Universidad de Gante. En 1820, fue elegido miembro de la Real Academia de Ciencias de Bruselas.
Los años posteriores los dedicó especialmente a la enseñanza y a la publicación de diversos tratados de matemáticas, física y astronomía.
Quetelet solía empezar su curso de historia de la ciencia con la siguiente observación:
“Cuanto más avanzan las ciencias, más invaden el dominio de la matemática, que actúa como una especie de punto de convergencia. Podemos juzgar el grado de perfección al que ha llegado una ciencia por la mayor o menor facilidad con la que se le pueden aplicar cálculos”.
En diciembre de 1823, Quetelet viajo a París, enviado por el gobierno belga, con el fin de estudiar técnicas de observación en astronomía. Sin embargo, esta visita de tres meses sirvió para que Quetelet conociera a Laplace, y fijase su atención en la teoría de las probabilidades . Más adelante, Quetelet hablaría de este modo de su experiencia con la estadística y la probabilidad:
“El azar, ese misterioso vocablo del que tanto se ha abusado, se debe considerar nada más que como un velo para nuestra ignorancia; es un espectro que domina de forma absoluta la mente común, acostumbrada a considerar los acontecimientos de un modo aislado, pero que queda reducido a nada ante el filósofo, cuyo ojo abarca largas series de eventos y cuya lucidez no se extravía en variaciones, que desaparecen cuando adquiere una perspectiva suficiente para aprehender las leyes de la naturaleza.”
En esencia, Quetelet negaba el papel del azar y lo sustituía por la idea de que incluso los fenómenos sociales poseen causas, y que las regularidades que presentan los resultados estadísticos se pueden emplear para desentrañar las reglas que subyacen al orden social.
Con la intención de probar la validez de su punto de vista estadístico, Quetelet puso en marcha un ambicioso proyecto de recopilación de miles de medidas relacionadas con el cuerpo humano. Estudió, por ejemplo, la distribución de medidas del pecho de 5.738 soldados escoceses, y de la altura de 100.000 reclutas franceses, y representó gráficamente la frecuencia de aparición de cada rasgo humano.
Luego construyó curvas similares incluso para aquellos rasgos «morales» (según él los denominaba) de los que poseía suficientes datos. Entre estas cualidades se hallaba la propensión al comportamiento criminal, los suicidios y los matrimonios. Para su sorpresa, Quetelet descubrió que todas las características humanas siguen lo que ahora se denomina una distribución normal.
Ya se tratase de alturas, pesos, longitudes de extremidades o incluso cualidades intelectuales determinadas a través de los primeros tipos de tests psicológicos, una y otra vez aparecía el mismo tipo de curva. Hasta el momento, solía ser nombrada como curva de error, porque solía aparecer en cualquier tipo de errores de medida.
Quetelet consideró que el hecho de que las características humanas siguiesen la curva de los errores era indicativo de que el hombre medio (l’homme moyen) era lo que la naturaleza estaba tratando de generar. Según Quetelet, de igual modo que los errores de fabricación crearían una distribución de longitudes alrededor de la longitud promedio (correcta) de un clavo, los errores de la naturaleza estaban distribuidos alrededor de un tipo biológico preferible. Así, afirmó que las personas de una nación estaban agrupadas alrededor de su promedio, “de igual modo que los resultados de mediciones efectuadas sobre una misma persona, pero con instrumentos imprecisos que justifican el tamaño de la variación”.
Puesto que, evidentemente, es deseable que la sociedad “exista y se conserve”, de ello se deduce que el comportamiento promedio es el comportamiento correcto. De este modo, la física social de Quetelet se fundó en el concepto de hombre medio:
“un individuo que, en un momento dado, es el epítome de todas las cualidades del hombre promedio, representaría toda la grandeza, belleza y bondad del ser”.
Esta inquietante veneración de la uniformidad tiene su corolario en el aborrecimiento de todas las singularidades:
“Las desviaciones más o menos pronunciadas del promedio han constituido […] la fealdad en el cuerpo como el vicio en la moral, y un estado enfermizo de la constitución general.”
La idea de que la perfección moral y física de la humanidad queda reflejada en la conformidad a unos datos matemáticos se remonta al Renacimiento, cuando, además, llegaron a definirse los instrumentos para cimentar la perfección.
Desde nuestra limitada perspectiva actual, el hecho sorprendente consiste en que prácticamente todos los detalles medibles de los seres humanos (de una raza determinada) están distribuidos según un solo tipo de función matemática.
Figura 6.16: Tabla de estaturas de 26.000 soldados americanos del ejercito del Norte durante la guerra civil (Phys. Soc, i., p. 131; Anthropom., p. 259).
Figura 6.17: Tabla de medidas alrededor del pecho, de los soldados del ejercito del Potomac (Phys. Soc, ii., 59; Anthropom., p. 289).
Figura 6.18: Tabla de las medidas de fuerza en hombres, estimadas mediante un dinamómetro (Anthropom., p. 365).
En un ejemplo descrito en un documento (Letters) en 1846, Quetelet comprobó que las alturas registradas de cien mil reclutas del ejército francés no se ajustaban con precisión a la distribución normal. Según los documentos oficiales, había \(28.620\) hombres sobre cien mil que se encontraban por debajo de \(1.57\) metros. Concretamente, existían excesivos individuos en las clases (intervalos) correspondientes a las alturas entre \(1.5\) y \(1.57\), y demasiados entre \(1.57\) y \(1.597\) metros. Precisamente, \(1.57\) era la talla que servía para excluir del servició militar. Con los cálculos correspondientes, se comprobó que \(2275\) individuos habían sido excluídos ilegalmente (habrían pagado a quien midiera para que les anotara una estatura más baja).
Pero la regularidad en la distribución de los datos no sólo se adaptaba a las características humanas. De los amplios estudios que Quetelet realizó sobre las estadísticas disponibles, observó que existian leyes que se adaptaban muy bien a otro tipo de situaciones, como el número de crímenes, de personas con enfermedad mental… En (Caponi 2013) podemos leer:
“Quetelet concluye, a partir de estudios cuantitativos y de la observación de datos empíricos, que cada año se repite, de manera exacta, el mismo número de crímenes, de suicidios, de matrimonios y de nacimientos en una población determinada. Analizando las estadísticas del ejército concluirá que los soldados presentaban, año tras año, las mismas medidas de peso, altura, tamaño de tórax. Observa que el número de alienados, internados en los asilos, se mantiene asombrosamente constante y que el tipo de crímenes y las penas aplicadas permanecen regulares según los datos suministrados por los registros civiles y los psiquiátricos. El único modo de poder explicar esas constantes que tanto seducían a Quetelet era analizar cada uno de estos hechos desde una perspectiva, ya no individual, sino poblacional. No se trataba de entender por qué razón ocurría cierto tipo de crimen y no otro, o por qué motivo un individuo presentaba una altura o peso determinados. Se trataba de explicar la repetición de fenómenos que, por su constancia, parecían indicar alguna fuerza común a todos ellos, una causa común capaz de mantener ese equilibrio, la acción de leyes tan regulares como las que rigen los astros o la caída de los cuerpos.”
Crimenes-francia-Quetelet.xlsx y `duelos-quetelet.xlsx).
## # A tibble: 12 x 7
## `Muerte Por` `1826` `1827` `1828` `1829` `1830`
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 Crimenes en~ 241 234 227 231 205
## 2 pistola 56 64 60 61 57
## 3 espada, sab~ 15 7 8 7 12
## 4 cuchillo 33 40 34 46 44
## 5 bastones 23 28 31 24 12
## 6 piedras 20 20 21 21 11
## 7 instrumento~ 35 40 42 45 46
## 8 estrangulam~ 2 5 2 2 2
## 9 precipitaci~ 6 16 6 1 4
## 10 patadas y g~ 28 12 21 23 17
## 11 fuego 0 1 0 1 0
## 12 desconocidas 17 1 2 0 2
## # ... with 1 more variable: `1831` <dbl>## # A tibble: 5 x 5
## año `muertes accide~ suicidios `duelos con mue~
## <dbl> <dbl> <dbl> <dbl>
## 1 1827 4744 1542 19
## 2 1828 4855 1754 29
## 3 1829 5048 1904 13
## 4 830 4478 1756 20
## 5 1831 5045 2084 23
## # ... with 1 more variable: `duelos sin muerte` <dbl>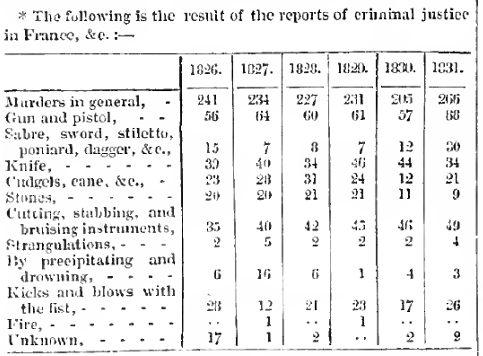
Figura 6.19: Tabla original del trabajo de Quetelet.

Figura 6.20: Tabla original del trabajo de Quetelet.
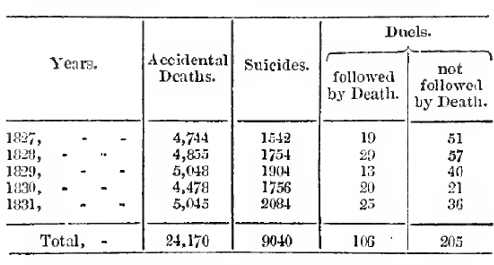
Figura 6.21: Tabla original del trabajo de Quetelet.
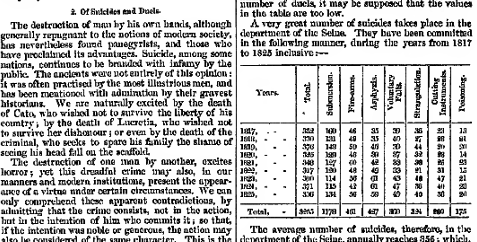
Figura 6.22: Tabla original del trabajo de Quetelet. Observemos que los números, año a año, son casi similares, lo cual provocó el asombro de Quetelet (y de cualquiera).
“Hoy en día, la idea de los promedios se da por sentada. Forman parte del zumbido de los medios de comunicación diarios. Mientras escribo esto, el New York Times del día reporta la cantidad promedio de deuda estudiantil, el número promedio de televidentes de la televisión en horario de máxima audiencia y el salario promedio de los médicos. Pero cada vez que Quetelet revelaba un nuevo promedio, el público se asombraba. Por ejemplo, Quetelet mostró que la tasa promedio de suicidio era relativamente estable de año en año. Aunque esto no sería una noticia sorprendente en estos días, en la década de 1830 el suicidio fue visto como una decisión privada altamente irracional que no podía ajustarse a un patrón más profundo. En cambio, Quetelet mostró que los suicidios ocurrían con regularidad confiable y consistente. Y no sólo eso: Afirmó que la estabilidad de los hechos indicaba que todo el mundo tiene una propensión promedio al suicidio.”
— Todd Rose, 2016. The Atlantic
Académicos y pensadores en todos los campos aclamaron a Quetelet como un genio para descubrir las leyes ocultas que gobiernan la sociedad. Florence Nightingale adoptó sus ideas en enfermería, declarando que el hombre promedio encarnaba la “Voluntad de Dios”. Karl Marx se basó también en las ideas de Quetelet, afirmando que “el hombre común” demostraba la existencia del determinismo histórico. El físico James Maxwell se inspiró en las matemáticas de Quetelet para formular la teoría clásica de la mecánica del gas. El médico John Snow utilizó las ideas de Quetelet para luchar contra el cólera en Londres, marcando el inicio del campo de la salud pública. Wilhelm Wundt, padre de la psicología experimental, leyó a Quetelet y proclamó: “Se puede afirmar sin exagerar que de los promedios estadísticos se puede aprender más psicología que de todos los filósofos, excepto de Aristóteles”.
Según Quetelet, el hombre medio está impuesto de tal forma que no es posible realizar modificaciones. No solo las características fisiológicas como la cantidad de respiraciones o de pulsaciones por minuto, la altura o la fuerza que podemos alcanzar se definen en relación a la constancia representada por el hombre medio, sino que también hechos sociales tan variados como la cantidad de crímenes, matrimonios, casos de alienación mental, suicidios, ya están preestablecidos, de modo tal que escapa de nuestras manos cualquier modificación.
“Podemos enumerar anticipadamente cuántos individuos mancharán sus manos con la sangre de sus semejantes, cuántos serán falsificadores, cuántos envenenadores, con tanta precisión como podemos enumerar la cantidad de nacimientos y muertes que ocurrirán en una sociedad. La sociedad contiene en ella los gérmenes de todos los crímenes que se cometerán, al mismo tiempo que las condiciones para que ellos ocurran. Es ella quien prepara sus crímenes, y el culpable no es más que el instrumento que los ejecuta.
— Quetelet, 1848, p.315.
De esta forma, el ‘libre albedrío’ no es más que un obstáculo para la comprensión de las leyes que rigen las constantes biológicas y sociales. Quetelet no creía que nuestros actos estuviesen predeterminados, sino que, a pesar de la libertad del individuo, las acciones de unos y otros se mezclarían y se verían compensadas, encadenándose una permanencia de los hechos sociales año tras año. De nada serviría que nos neguemos a provocar un crimen; este acto de libertad será compensado con la acción contraria, posibilitando que se realice la natural tendencia a la constancia y a la repetición.
References
Caponi, Sandra. 2013. “Quetelet, El Hombre Medio Y El Saber Médico.” História, Ciências, Saúde-Manguinhos 20 (3). Fundação Oswaldo Cruz.