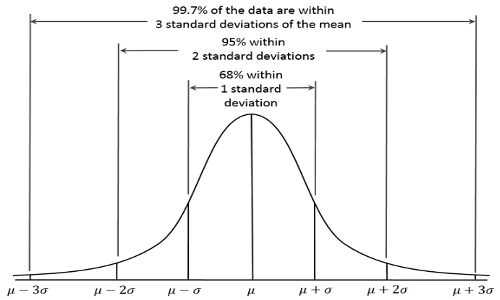
6.1 Ejemplos de la distribución normal
“muchos sucesos que, por su naturaleza, parecen caprichosos e inciertos, y para los cuales en ningún caso individual existe grado obtenible de conocimientos que nos permita preverlos, ocurren con un grado de regularidad que raya lo matemático, si se tienen en cuenta cifras considerables”
— John Stuart Mill (Un sistema de la lógica, 1862)
Así como hemos visto que hay otros casos de variables muy representativas de un conjunto de situaciones, como las leyes de potencias, la distribución normal o Gaussiana aparece en muchas más ocasiones en la práctica, debido, entre otros motivos, al teorema central del límite (al final de este tema). Veamos ahora unos cuantos ejemplos de variables que siguen esta ley.
6.1.1 La mecánica de los gases de Maxwell
Fue la obra del astrónomo Quetelet (más abajo) quien puso a James Clerk Maxwell (1831-1879) en el camino de la mecánica estadística: las moleculas de un gas son como los individuos de una población, ya que el desorden a escala individual se transforma en orden a escala poblacional.
Lo que importa de los movimientos de las partículas de gas, afirmó Maxwell, son dos cosas: la velocidad media a la que se mueve cada partícula —la cual determina su energía cinética media— y cuánto se aparta de esa media por arriba o por abajo. Maxwell intuyó que la distribución de velocidades semeja el tipo de curva en forma de campana. La curva de Maxwell indica cuántas partículas de gas se mueven a una velocidad determinada y se eleva suavemente desde velocidades bajas, alcanza el pico en la media, y vuelve a descender suavemente hacia las velocidades altas. Esta distribución muestra que muy pocas partículas alcanzan velocidades mucho más altas que el promedio. Maxwell dijo que lo importante no es la trayectoria precisa de todas las partículas del gas, sino su comportamiento medio. Maxwell imaginó un enjambre de abejas: las abejas zumban furiosamente en todas direcciones, pero el propio enjambre se mantiene estacionario, porque, teniendo en cuenta el promedio de sus vuelos, no es más probable que las abejas vuelen en una dirección que en otra. (Ball 2004)
La curva de Maxwell indica cuántas partículas de gas se mueven a una velocidad determinada y se eleva suavemente desde velocidades bajas, alcanza el pico en la media, y vuelve a descender suavemente hacia las velocidades altas. Esta distribución muestra que la mayoría de las partículas se mueven a una velocidad alrededor del promedio.
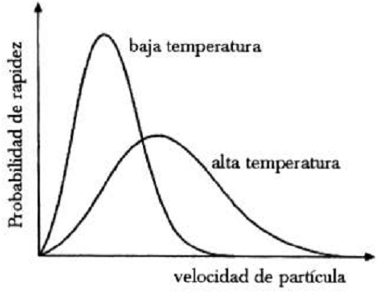
Figura 6.2: Distribución del movimiento de las moleculas de los gases.
6.1.2 Los datos antropométricos en los seres humanos
Escuchemos (y veamos) con detenimiento esta escena de El protegido (Unbreakable, 2000):
En esta escena, Samuel L. Jackson es un hombre con osteogénesis imperfecta, al cual le apodaron de pequeño “Don cristal”. Es una persona que ha tenido múltiples fracturas, muy débil. Piensa que él se encuentra a un extremo (de un ‘espectro’, le llama. Sería una forma particular de llamar a una distribución), y, al otro lado de un punto medio (un eje de referencia) podría existir otra persona que nunca se lesione, que no enferme… Bruce Willis permanece callado, porque al principio de la película hemos visto como iba en un tren que ha descarrilado y matado a todos sus ocupantes, excepto a él, que no tenía un solo rasguño.
¿Podemos suponer que, si existe una persona con unas determinadas características -llamemos ‘extremas’-, existirá otro con las mismas características ‘opuestas’? Por ejemplo, si existe un ‘genio del mal’, ¿existe un ‘genio del bien’? ¿Si existen personas muy altas en una población, necesariamente tienen que existir personas muy bajas? E incluso más: ¿el número de personas muy altas coincide con el número de personas muy bajas? ¿El número de personas extremadamente inteligentes coincide con el número de personas extremadamente poco inteligentes?…
El primero que respondió a este tipo de preguntas fue Adolphe Quetelet. Fue el primero en advertir que los datos antropométricos de los individuos de una misma población, raza, sexo y edad, constituyen una variable normal.
Para verlo con un ejemplo, elegimos el fichero de datos “body_dat.csv”, cogido de http://ww2.amstat.org/publications/jse/v11n2/datasets.heinz.html
El fichero consta de la medición de 25 Variables en 507 individuos (247 hombres y 260 mujeres, principalmente de entre 20 y 30 años de edad, todos haciendo ejercicio varias horas a la semana). Las mediciones fueron tomadas inicialmente for Grete Heinz y Louis J. Peterson en la Universidad Estatal de San José (USA) y en la Escuela de Postgrado Nval de Monterrey, California. Más tarde, se tomaron mediciones en centros de salud y acondicionamiento físico de California. La siguiente es la descripción del fichero por columnas:
# Columnas Variable
#
# Medidas esqueléticas:
#
# 1 - 4 Diámetro biacromial
# 6 - 9 Diámetro biológico, o "anchura pélvica"
# 11 - 14 Diámetro bitrocantéreo
# 16 - 19 Profundidad del pecho entre la
# columna vertebral
# y esternón a la altura de los pezones
# 21 - 24 Diámetro del pecho a nivel del pezón
# 26 - 29 Diámetro del codo,
# suma de dos codos
# 31 - 34 Diámetro de muñeca,
# suma de dos muñecas
# 36 - 39 Diámetro de rodilla,
# suma de dos rodillas
# 41 - 44 Diámetro del tobillo,
# suma de dos tobillos
#
# Medidas de circunferencia:
#
# 46 - 50 Circunferencia del hombro
# sobre los músculos deltoides
# 52 - 56 Perímetro torácico, línea de los
# pezones en los hombres y
# justo por encima del pecho
# 58 - 62 Cincha de la cintura, parte
# más estrecha del torso por
# debajo de la caja torácica
# 64 - 68 Circunferencia del ombligo
# (o "abdominal")
# en el ombligo y la
# cresta ilíaca
# 70 - 74 Cincha de la cadera al nivel
# del diámetro bitrocantéreo
# 76 - 79 Circunferencia del muslo
# por debajo del pliegue glúteo,
# promedio de dcha. e izda.
# 81 - 84 Cincha del bíceps, flexionada,
# promedio de cinchas
# derecha e izquierda
# 86 - 89 Cincha del antebrazo, extendida,
# palma hacia arriba, promedio
# de circunferencia derecha
# e izquierda
# 91 - 94 Cincha de la rodilla sobre
# la rótula, posición
# ligeramente flexionada, promedio
# 96 - 99 circunferencia máxima de la
# pantorrilla, promedio de
# circunferencias derecha e izquierda
# 101 -104 Circunferencia mínima del tobillo,
# media de cir. derecha e izda.
# 106 -109 circunferencia mínima de muñeca,
# promedio de cir. derecha e izda.
#
# Otras medidas:
#
# 111-114 Edad (años)
# 116-120 Peso (kg)
# 122-126 Altura (cm)
# 128 Género (1 - hombre, 0 - mujer)
#
# Las primeras 21 variables
# se miden en centímetros (cm).
#
# Los valores están separados por
# espacios en blanco. No faltan valores. A continuación, seleccionamos 8 variables y dibujamos la estimación de la densidad, diferenciándolas por sexos. Compruébese que siempre sale la campana de Gauss.
Ejercicio: En España, la estatura media de los hombres mayores de 18 años es de 177.7 cm y desviación típica de 5.9, mientras que en las mujeres la media es 164.7 y desviación típica 5.4. Calcular:
Probabilidad de que tu vecino tenga un hijo que sea igual o más alto que Pau Gasol (213cm)
Probabilidad de que su hermana sea igual o más alta que Nicole Kidman (180cm).
Si una mujer está en el percentil 85 de estatura, ¿cuánto mide?
Un hombre mide 190 cm y una mujer 178. ¿Cuál de los dos ocuparía la mayor posición dentro de su grupo, si clasificamos las alturas de menor a mayor?1 y 2. Dibujamos y hacemos las cuentas con R:
library(mosaic)
plotDist("norm", mean = 176.6, sd = 5.9, groups = x > 213,
type = "h")
p1 = (1 - pnorm(200, mean = 176.6, sd = 5.9))La probabilidad de ser más alto (o igual) que Pau Gasol es el área a la derecha del valor 213cm. Gráficamente, no se ve destacada área ninguna, aunque la hay. Su valor es lo que llamamos \(p1\) y que calculamos directamente con R mediante 1-pnorm(200,mean=176.6,sd=5.9).
library(mosaic)
plotDist("norm", mean = 164.7, sd = 5.4, groups = x > 180,
type = "h")
p2 = 1 - pnorm(180, mean = 164.7, sd = 5.4)La probabilidad de ser más alta que Nicole Kidman es el área (en rosa) a la derecha de 180cm, cuyo valor le llamamos \(p2\).
- y 2. Calculando con R, los valores son \(0.00003652\) y \(0.0023033\).
Apróximadamente, en España hay 46 millones de habitantes, de los cuales un 85 por ciento son mayores de 18 años. Supongamos que la mitad son hombres y la mitad son mujeres. Se obtiene una cantidad aproximada de 19.550.000 hombres o mujeres. Multiplicando por las probabilidades obtenidas, estimamos que el número de hombres con estatura mayor o igual a Pau Gasol es \(714.13\), y el número de mujeres con estatura mayor o igual que la de Nicole Kidman es \(45028.8\), más o menos.
- Se calcula como
p85 = qnorm(0.85, mean = 164.7, sd = 5.4)El valor es 170.2967.
- Para realizar una comparación entre dos valores que pertenecen a distribuciones normales diferentes, debemos tipificar ambos valores.
Si un hombre mide \(190\) cm, su puntuación tipificada es \(\dfrac{190-177.7}{5.9}=2.084\), y si una mujer mide \(178\), su puntuación tipificada es \(\dfrac{178-164.7}{5.4}=2.4629\).
Directamente, observamos que la mujer ocupa una mejor posición dentro del grupo “conjunto”, esto es una distribución normal con media cero y desviación típica 1.
6.1.3 La morfología del cerebro
En la página web cultura colectiva podemos leer lo siguiente:
“Una de las preguntas más comunes con respecto a las particularidades del cerebro radica en la diferencia que existe entre sexos. Tradicionalmente, distintos estudios científicos consideran que existen desigualdades insalvables entre los cerebros de hombres y mujeres. Tales diferencias se han utilizado a través de la historia para justificar el comportamiento de uno y otro sexo, estableciendo estereotipos entre la mentalidad masculina y femenina.
A pesar de que la ciencia médica consideraba en el pasado que no existían diferencias significativas entre ambos cerebros, el estudio más ambicioso jamás realizado para descubrir distinciones en la anatomía cerebral entre hombre y mujer arrojó resultados que podrían cambiar la forma en que comprendemos a cada sexo a partir de su pensamiento. El doctor Stuart Ritchie, especialista en Psicología de la Universidad de Edimburgo, se valió de más de 500 mil datos disponibles en el UK Biobank (una iniciativa científica del Reino Unido para la recopilación de información relativa a los órganos del cuerpo humano) para escanear cerebros y descifrar si la información arrojada a través de resonancias magnéticas era suficiente para descubrir si se trataba de un hombre o una mujer.
La amígdala, el hipocampo, el cuerpo estriado y el tálamo de los hombres son visiblemente más grandes que las mismas regiones en las mujeres. No obstante, la anatomía del sistema nervioso central femenino posee una corteza cerebral más gruesa que la masculina, un elemento que parece decisivo en la obtención de un resultado más alto en las pruebas de habilidades cognitivas e inteligencia.
El resultado fue estadísticamente notorio: en cerca del \(77\%\) de los casos fue posible identificar correctamente el sexo del cerebro en cuestión. Según el estudio (Ritchie et al. 2017), la diferencia más significativa entre el sistema nervioso central de los sexos de nuestra especie está en el tamaño: los cerebros masculinos poseen un volumen mayor que los de su contraparte femenina, no sólo en el total de materia gris, también en áreas específicas del mismo."
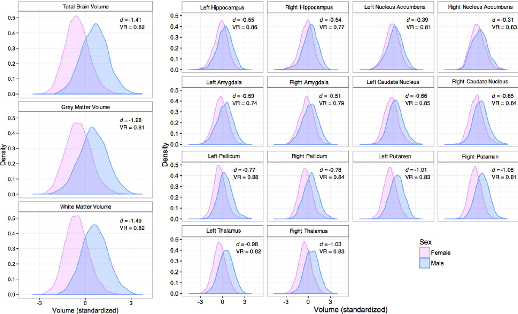
Figura 6.3: Gráfica del trabajo de Ritchie et al. (2017)., donde se observa que las características antropométricas del cerebro humano también siguen la distribución normal (algo que, evidentemente, Quetelet no llegó a comprobar)
6.1.4 Las características psico-sociales
Adolphe Quetelet fue también el primero en descubrir que, además de los caracteres antropométricos, los caracteres psicológicos y sociales de los seres humanos tienden a distribuirse como campanas de Gauss. La propensión a la violencia, a la aflicción, la empatía hacia los demás, el sentido del humor… Existe una mayoría de personas con características de este tipo en la media, disminuyendo la proporcion a medida que vamos hacia los extremos.
Veamos algunos ejemplos con datos concretos procedentes de estudios científicos.
En R, en el paquete Car, tenemos el archivo de datos Cowles que consta de 1421 filas y 4 columnas, con datos de interés psicológico para el voluntariado social.´Las gráficas por sexo aparecen en la Figura 6.4.
require(car)
data(Cowles)
Cowles$sexo=Cowles$sex
N=nrow(Cowles)
y=rep(0,N)
y1<-data.frame(y)
names(y1)<-"ceros"
Cowles2 <-bind_cols(Cowles, y1)
p1<-ggplot(Cowles2)+
geom_density(aes(x= neuroticism), adjust=2) +
aes(colour = sexo) +
labs(title="Inestabilidad Emocional", y=" ", x=" " ) +
theme(legend.position = "top") +
geom_point(aes(x=neuroticism, y=ceros), size=1)
p2<-ggplot(Cowles2)+
geom_density(aes(x= extraversion), adjust=2) +
aes(colour = sexo) +
labs(title="Extraversion", y=" ", x=" " ) +
theme(legend.position = "top") +
geom_point(aes(x=extraversion, y=ceros), size=1)
grid.arrange(p1,p2,ncol=2)
Figura 6.4: Densidad de los datos de Inestabilidad emocional y Extraversión, por sexos.
Los siguientes datos corresponden a un estudio descrito en (Kalichman and Rompa 1995): Sexual Compulsivity Scale. En los siguientes enlaces puede leerse la descripción de las preguntas y ver los datos. Descripcion y Datos. Las gráficas por sexo aparecen en la figura 6.5.
Figura 6.5: Densidad de los datos de la compulsividad sexual, por sexos.
De nuevo, campanas de Gauss para describir la distribución de los datos.
Otro ejemplo: el trabajo de (Hansenne et al. 2001), donde se detalla un cuestionario de 226 items del Inventario de Temperamento y Carácter (TCI, por sus siglas en inglés) para evaluar las siete dimensiones de la personalidad descritas por Cloninger (Cloninger et al. 1994). El cuestionario fue respondido por 322 ciudadanos Belgas. En este enlace: Datos_y_trabajo pueden descargarse el trabajo y los datos.
Análizamos 4 variables del estudio: Novelty Seeking (búsqueda de novedad) (NS), Harm Avoidance (evitación de daños) (HA), Reward dependence (búsqueda de recompensas) (RD) y Sentimentality (sentimentalismo) (RD1): gráficas 6.6 y 6.7.
Figura 6.6: Densidad de los datos de dos variables del estudio de Hansenne (2001), por sexos.
Figura 6.7: Densidad de los datos de otras dos variables del estudio de Hansenne (2001), por sexos.
De estos (y de otros muchos estudios publicados) parece concluirse también que las características psico-sociales de los seres humanos, correspondientes a una misma raza, cultura, población y sexo parecen venir descritas mediante leyes Gaussianas.
Retomemos ahora la pregunta que nos planteábamos tras ver la escena de “El protegido”: ¿es posible la existencia de personas opuestas, en cuanto a las características de "fragilidad", como expone el personaje interpretado por Samuel L. Jackson? Él es el hombre que ‘se rompe constantemente’. ¿Existe uno que ‘practicamente nunca se rompa’, que sería Bruce Willis?
Tenemos que darnos cuenta de que falla una hipótesis. Es la de encontrarnos en lo que, precisamente, se llama población normal, como sinónimo de común. El personaje de ‘Don Cristal’ no pertenece a la población más común, puesto que es una persona con una enfermedad genética, de la que tendríamos que estudiar sus características (por ejemplo, si esa población sigue o no una distribución normal). Pero, sin embargo, esta escena puede hacernos pensar en personas que a menudo conocemos. Por un lado, gente muy propensa a enfermedades, o a lesionarse, y a la vez gente que rara vez enferma, que se lesiona poco. El azar asociado a la campana de Gauss provoca que los extremos (a ambos lados) sean los más raros (los de menos probabilidad), frente al término medio, que es lo más común.
Por último, recordemos que, en el documental de la 2 que veíamos al principio de este capítulo, nos contaban que Gauss era un genio, y que pertenecía al dos por ciento de personas con cociente intelectual, digamos, “altísimo”. Los genios son aquellas personas con cociente intelectual extremo (al este, o sea a la derecha). En una distribución normal, los datos extremos, o las colas de la distribución, son los datos que están alejados \(2\sigma\) (dos desviaciones típicas) de la media. Tengamos en cuenta que, en una distribución normal cualquiera \(X\in N(\mu, \sigma)\), la probabilidad en los extremos o colas de la distribución es \((1-p)/2\), siendo \(p\) \[ p= P(\mu-2\sigma<X<\mu +2\sigma) \]
Recordemos las áreas en una distribución normal:
Figura 6.8: Áreas en la campana de Gauss.
Al “este” de la campana de Gauss están, como vemos, el dos por ciento: los superdotados intelectualmente, los más altos, los más destacados por alguna característica física o psico-social humana… Incluso, los humanos con instinto asesino:
6.1.5 El consumo de petroleo, gas, electricidad, de una ciudad, un pais, en un determinado periodo de tiempo
El consumo de petroleo (o gas, o electricidad, propano…) de una ciudad (ayuntamiento, urbanización, etc.) es la suma de los consumos individuales de las familias o particulares. Por ello, y debido al teorema central del límite (del que hablamos más adelante), la distribución de esta variable (consumo) va a seguir una distribución normal.
6.1.6 Los errores de medición
“Imaginemos, por ejemplo, que debe medir con mucha precisión la temperatura de un líquido en un recipiente. Puede utilizar un termómetro de alta precisión y tomar mil medidas a lo largo de un período de una hora. Debido a errores aleatorios y posiblemente a fluctuaciones en la temperatura, hallará que no todas las mediciones dan exactamente el mismo valor, sino que tienden a agruparse alrededor de un valor central; algunas mediciones dan un valor superior y otras, uno inferior. Si representa el número de veces que aparece cada medida en función de la temperatura, obtendrá el mismo tipo de curva en forma de campana que Quetelet halló para las características humanas. De hecho, cuanto mayor sea el número de mediciones efectuadas de cualquier magnitud física, más se aproximará la distribución de frecuencias a la curva normal. La influencia inmediata de este hecho en la cuestión de por qué las matemáticas son tan extraordinariamente eficaces es bastante espectacular: ¡incluso los errores humanos obedecen leyes matemáticas estrictas!” (Ball 2004)
El problema de los errores de medición era algo que preocupaba a los astrónomos desde siempre: al realizarse mediciones de, por ejemplo, distancias de la tierra a otros puntos del mapa celeste, estas no coincidan (las mediciones se realizaban desde diferentes puntos de la tierra en diferentes momentos pero, obviamente, al realizar las transformaciones matemáticas pertinentes, las mediciones deberían ser iguales, cosa que no ocurria). La teoría de los errores de medida fue iniciada por Galileo (1564-1642), que advirtió que estos errores eran simétricos, y que los errores pequeños se producen con más frecuencia que los grandes. Esta idea fue apoyada por otros muchos científicos, en su mayoría astrónomos; como, por ejemplo, Ticho Brahe (1546–1601), quien encontró que cada medida tiene un posible error. Brahe fue quien intuyó que, debido a estos errores, la medida se podía precisar realizando varias observaciones y calculando la media aritmética.
R. Cotes (1682–1716), T. Simpson (1710–1761) y Daniel Bernoulli fueron los primeros en tratar matemáticamente la teoría de la medida de errores Cotes opinaba que los errores se distribuían uniformemente, es decir, que se cometían tantos errores pequeños como grandes. Más adelante, Laplace afirmó que los errores de medida observados eran la suma de una gran cantidad de pequeños errores; si estos errores tenían una distribución normal, su suma también debería tenerla. Como estimación del valor desconocido del error, Laplace sugirió tomar el valor que minimiza la cantidad que es igual a la mediana de las observaciones realizadas. Sin embargo, su trabajo no alcanzó mucha difusión, debido a las aportaciones de Gauss y Legendre (1752–1833), que propusieron y desarrollaron el método de mínimos cuadrados. Gauss demostró que, bajo ciertas condiciones generales, la función de densidad de los errores de medida tiene la forma de la distribución normal. (Salinero 2006)
6.1.7 Duración de un embarazo
Se sabe que es una variable aproximadamente normal, con una media de 266 días y una desviación típica de 16 (Moore and Kirkland 2007).
6.1.8 Velocidad de las Galaxias
En el trabajo de (Roeder 1990) se puede ver la distribución que sigue el conjunto de velocidades de 82 galaxias de la Corona Boreal.
En el paquete MASS de R se encuentra este conjunto de datos. Se trata de la velocidad en km/seg de 82 galaxias de seis secciones cónicas bien separadas, de un estudio de la región de Corona Borealis. Como se ve, no hay una única distribución normal, sino lo que se conoce como una mixtura de distribuciones, donde cada una de las distribuciones que se “mezclan” aparece representada por la moda (máximo). Según explican en el trabajo de (Roeder 1990), esa multimodalidad es evidencia de vacíos y superclusters en el universo lejano (obvio para cualquiera).
library(MASS)
gal <- galaxies/1000
# c(width.SJ(gal, method = "dpi"), width.SJ(gal))
plot(x = c(5, 40), y = c(0, 0.2), type = "n", bty = "l",
xlab = "velocidad (1000km/s)", ylab = "densidad")
rug(gal)
lines(density(gal, width = 3.25, n = 200), lty = 1)
lines(density(gal, width = 2.56, n = 200), lty = 3)
Figura 6.9: Densidad del conjunto de datos correspondiente a la velocidad de 82 galaxias.
6.1.9 La ley de Farr de las epidemias
(Brownlee 1915)
William Farr, el famoso epidemiólogo inglés (1807–1883), postuló que las epidemias tienden a crecer y caer con un patron aproximadamente simétrico, del tipo Campana de Gauss. La idea fue resucitada por Brownlee a principios del siglo XX. Un artículo famoso sobre la epidemia del sida (Bregman, Langmuir, and others 1990) analizó 200.000 casos desde 1982 hasta 1988, estimando que la enfermedad tendería a desaparecer hacia 1994. Sin embargo, artículos posteriores adviertieron de la no consideración del periodo de incubación de la enfermedad, lo que debería hacer construir una curva desde diez años más atrás y hasta después del año 2000.
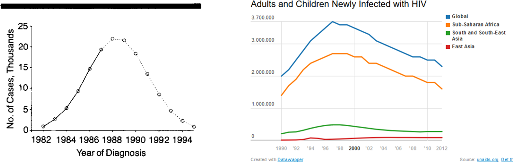
Figura 6.10: Izquierda: Figura original del artículo de Bregman. Proyección de casos hasta el 94. Derecha: datos recientes.
6.1.10 Crecimiento de las plantas
Las reglas matemáticas que rigen el crecimiento de las plantas son similares a cómo brotan conexiones en las células cerebrales, según descubrieron científicos del Salk Institute, según puede leerse en el trabajo de (Conn et al. 2017).
6.1.11 Votos en las elecciones: Putin contra Gauss
Gracias a la campana de Gauss (entre otros detalles), se sabe desde hace tiempo que Putin gana las elecciones haciendo trampas: la curva de distribución de la variable mesas electorales según su participación no sigue una curva gaussiana. Existe una amplia cantidad de artículos científicos donde se demuestran las constantes irregularidades en los procesos electorales en Rusia. Ver, por ejemplo, (Klimek et al. 2012)
6.1.12 Los seis grados de separación
Esta teoría la propuso el escritor Frigyes Karinthy en 1930, y viene a decir que se puede acceder a cualquier persona del planeta en sólo seis (o menos) pasos o conexiones, o dicho de otra manera:
Cualquier persona del mundo estaría unida a nosotros a través de una cadena de conocidos de no más de cinco intermediarios o intermediarias, conectándonos con sólo seis enlaces, pasos o saltos.
Existe una película sobre este tema, llamada precisamente Seis grados de Separación
Esta teoría hizo famoso en los años 90 el llamado “juego de Kevin Bacon”, que se convirtió en un fenómeno popular entre los amantes del cine, y predijo la web social de conexiones en línea que hoy encontramos en Facebook o Twitter.
El juego requiere que quienes participan en él vinculen a celebridades con Bacon, en la menor cantidad de pasos posible, a través de las películas que tienen en común. Mientras más extraña o aleatoria sea la celebridad, mejor. Por ejemplo, O.J. Simpson estuvo en The Naked Gun 33 1/3 con Olympia Dukakis, quien estuvo en Picture Perfect con Kevin Bacon.
Figura 6.11: Número de Bacon de Carmen de Mairena.
Búsquese usted mismo: en esta página
En 1967, el psicólogo norteamericano Stanley Milgram realizó el denominado experimento del ‘mundo pequeño’ para intentar demostrar la teoría.
El experimento consistió en seleccionar al azar a varias personas del Medio Oeste para que enviaran un paquete a un extraño situado en Massachussetts, a varios miles de kilómetros de distancia. Las personas remitentes sabían el nombre y la dirección aproximada, y tenían que enviar el paquete a una persona que ellos conocieran directamente y que pensasen que fuese la que más probabilidades tenía, de entre todo su círculo de amistades, de conocer directamente al destinatario. Esta persona tendría que hacer lo mismo, y así sucesivamente, hasta que el paquete fuera entregado personalmente a su destinatario final en la Costa Este.
Para sorpresa de todos, Milgram comprobó que hacía falta, en promedio, entre cinco y siete intermediarios o intermediarias para hacer llegar el paquete a esa persona desconocida. De nuevo aparece la curva normal. La media o mediana es tres, y hay tanta probabilidad de que haya un grado o dos más como un grado o dos menos.
En la reciente película Experimenter: la historia de Stanley Milgram se habla de este experimento, y muchos otros que hizo famosos el doctor Milgram, de los cuales tal vez el más conocido sea el de la capacidad de obediencia del ser humano (aunque sea para ejercer dolor contra otro ser humano).
En 2003, el sociólogo Duncan J. Watts recogió la teoría actualizada en su libro Seis grados: la ciencia de las redes en la era conectada del acceso. Watts intentó probar la teoría de nuevo, esta vez a través del correo electrónico con personas de todo el mundo. El resultado promedió de nuevo los famosos seis grados.
El estudio más extenso hasta la fecha sobre la teoría de los seis grados de separación lo realizó Facebook en 2011 (“Anatomy of Facebook”): el estudio se realizó con todas las personas usuarias activas de su página en esa fecha (que rondaban los 720 millones, alrededor de un \(10\%\) de la población mundial. Consistió en analizar el conjunto de amigos o amigas en común de las personas usuarias de la página, para promediar cuántos eslabones hay entre dos usuarios cualesquiera de la página. El estudio mostró que un \(99'6\%\) de pares de personas usuarias estuvieron conectados por cinco grados de separación (\(4.75\) eslabones de promedio).
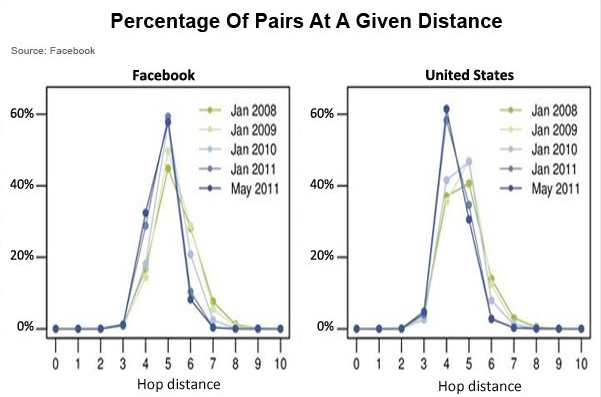
Figura 6.12: Estudio de los usuarios de Facebook.
6.1.13 La psicofísica
La psicofísica fue introducida en 1850 por Gustav Fechner (Polonia, 1801 - Alemania, 1887), quien se preguntaba hasta qué punto una persona puede distinguir objetos de pesos ligeramente diferentes.
Figura 6.13: Gustav Fechner, a quien se le atribuye la introducción del concepto de mediana.
Posteriormente, Charles S. Peirce (filósofo, matemático y padre de la semiótica; 1839-1914) y un alumno suyo, Joseph Jastrow (1863-1944), hicieron experimentos “ciegos” (el sujeto no sabía si se le daba una caja más pesada o liviana). Es importante destacar que este fue el primer experimento en que la serie de pruebas fue determinada por un casualizador artificial. (Peirce and Jastrow 1884)
Figura 6.14: Charles Sander Pierce.
Peirce y Jastrow se preguntaban: ¿existe, en una persona, una ley general para discriminar?.
Sí, la curva de gauss. La variación mide la sensibilidad de un individuo. Desde el punto de vista histórico, esta comprobación significó una mayor autonomía a las leyes estadísticas. Estas son también capaces de medir una realidad psicológica de la cual ni siquiera tenemos conciencia. La sensibilidad alrededor del peso real sigue la curva de Gauss. Tanta gente se equivoca “por abajo” como “por arriba”, y menos cuanto más se aleja del peso real.
Peirce pensó que su descubrimiento de que no existe un umbral mínimo podía explicar la intuición femenina y la telepatía (tenues sensaciones de las que no tenemos plena conciencia). Posteriormente, se fundó en Londres, en 1882, la sociedad de investigación psíquica. Sus miembros deseaban reemplazar por un estudio científico el entusiasmo vulgar por la figura del medium: en lugar de suponer que había comunicación con los muertes, se suponía que podía existir transferencia de pensamiento entre personas vivas.
References
Ball, Philip. 2004. Masa Crítica. Cambio, Caos y Complejidad. Turner Publicaciones.
Bregman, Dennis J, Alexander D Langmuir, and others. 1990. “Farr’s Law Applied to Aids Projections.” Jama 263 (11). American Medical Association: 1522–5.
Brownlee, John. 1915. “Historical Note on Farr’s Theory of the Epidemic.” British Medical Journal 2 (2850). BMJ Publishing Group: 250.
Cloninger, C Robert, Thomas R Przybeck, Dragan M Svrakic, and Richard D Wetzel. 1994. “The Temperament and Character Inventory (Tci): A Guide to Its Development and Use.” Center for Psychobiology of Personality, Washington University St. Louis, MO.
Conn, Adam, Ullas V Pedmale, Joanne Chory, Charles F Stevens, and Saket Navlakha. 2017. “A Statistical Description of Plant Shoot Architecture.” Current Biology 27 (14). Elsevier: 2078–88.
Hansenne, Michel, Olivier Le Bon, Anne Gauthier, and Marc Ansseau. 2001. “Belgian Normative Data of the Temperament and Character Inventory.” European Journal of Psychological Assessment 17 (1). Hogrefe & Huber Publishers: 56.
Kalichman, Seth C, and David Rompa. 1995. “Sexual Sensation Seeking and Sexual Compulsivity Scales: Validity, and Predicting Hiv Risk Behavior.” Journal of Personality Assessment 65 (3). Taylor & Francis: 586–601.
Klimek, Peter, Yuri Yegorov, Rudolf Hanel, and Stefan Thurner. 2012. “Statistical Detection of Systematic Election Irregularities.” Proceedings of the National Academy of Sciences 109 (41). National Acad Sciences: 16469–73.
Moore, David S, and Stephane Kirkland. 2007. The Basic Practice of Statistics. Vol. 2. WH Freeman New York.
Peirce, Charles Sanders, and Joseph Jastrow. 1884. “On Small Differences in Sensation.”
Ritchie, Stuart J, Simon R Cox, Xueyi Shen, Michael V Lombardo, Lianne Maria Reus, Clara Alloza, Matthew A Harris, et al. 2017. “Sex Differences in the Adult Human Brain: Evidence from 5,216 Uk Biobank Participants.” bioRxiv. Cold Spring Harbor Labs Journals, 123729.
Roeder, Kathryn. 1990. “Density Estimation with Confidence Sets Exemplified by Superclusters and Voids in the Galaxies.” Journal of the American Statistical Association 85 (411). Taylor & Francis: 617–24.
Salinero, Pablo. 2006. “Historia de La Teoría de La Probabilidad.” Ver Www. Uam. Es/Personal_pdi/Ciencias/Ezuazua/Informweb/Trabajosdehistoria/S Alinero_probabilidad. Pdf. Consultado El 20: 1–21.