3.5 Dependencia estadística entre variables
Cuando consideramos dos variables \(X\) e \(Y\) midiendo dos características diferentes en una misma población, nos interesa estudiar si existe relación entre las mismas. Una primera forma de verlo es mediante el diagrama de dispersión o nube de puntos.
3.5.1 Diagrama de dispersión.
Consiste en representar, en un plano, las coordenadas \((x_i,y_j)\) correspondiente a los valores de \(X\) e \(Y\), respectivamente.
HistData tenemos el conjunto de datos Galton. Este conjunto de datos (tomados en 1886 por Francis Galton) corresponde a las estaturas de 928 adultos varones (variable \(Y\)) y la estatura media del padre y la madre (variable \(X\)).
data(Galton)
Gl<-data.frame(Galton)
ggplot()+
geom_point(data=Gl,
aes(x=parent, y=child),
size=3, color="blue")Figura 3.5: Datos originales estudiados por Galton.
Mediante el gráfico 3.5, podemos ver que, a medida que el padre y la madre tienen estatura mayor (eje \(X\): media de las alturas) los hijos tienen, de manera general, también mayor estatura. Se observa, por lo tanto, un tipo de relación lineal creciente. Este gráfico se ha realizado mediante la librería ggplot2 que, obviamente, hay que llamarlo primero, mediante library(ggplot2). La resolución gráfica es mucho mejor que con los comandos básicos de R, que serían, simplemente:
data(Galton)
plot(Galton$parent, Galton$child, col="blue")Figura 3.6: Diagrama de dispersión mediante plot.
Como vemos, el gráfico 3.6 es igual que el anterior, pero más cutrillo.
HSAUR podemos encontrar el conjunto de datos water, correspondiente a la mortalidad y dureza del agua en 61 ciudades de Inglaterra y Gales durante los años 1958 a 1964. Se trata de 61 observaciones de 4 variables: \(location\) (un factor con niveles North y South), \(town\) con el nombre de la ciudad, \(X\) correspondiente a la mortalidad (mortalidad anual media por cada 100.000 varones) e \(Y\) correspondiente a la dureza del agua (concentración de calcio en partes por millón) (Hand et al. 1993).
library(HSAUR)
data("water", package = "HSAUR")
mort<-data.frame(water)
ggplot()+
geom_point( data=mort,
aes(x=hardness, y=mortality, colour=location))Figura 3.7: Datos relacionando dureza del agua y mortalidad.
La estructura de la nube de puntos deja entrever que, a mayor dureza del agua (mayor concentración de calcio), la mortalidad disminuye. Es, al contrario que antes, una relación lineal decreciente.
3.5.2 Covarianza. Correlación lineal.
Sir Francis Galton fue geógrafo, meteorólogo, antropólogo y estadístico, e introdujo por primera vez el término correlación, de la siguiente forma:
“La longitud del cúbito [el antebrazo] está correlacionada con la estatura, ya que un cúbito largo implica en general un hombre alto. Si la correlación entre ellas es muy próxima, un cubito muy largo implicaría una gran estatura; en cambio, si no lo es tanto, un cúbito muy largo estaría asociado en promedio con una estatura simplemente alta, pero no muy alta; mientras que, si la correlación fuese nula, un cubito muy largo no estaría asociado con ninguna estatura en particular y, por consiguiente, en promedio, con la mediocridad.”
Este discurso original se enmarcó dentro de su trabajo como científico, interesado en estimar la estatura de las poblaciones, a partir de los huesos encontrados en excavaciones. Antes de definir el concepto matemático de correlación, necesitamos estudiar la llamada covarianza, o medida de variabilidad conjunta entre dos variables.
La covarianza de una variable bidimensional \((X,Y)\) que toma valores \(\{(x_i,y_i)\}_{i=1}^n\) viene dada por la expresión
\[ S_{XY}=\frac{1}{n}\cdot \sum_{i=1}^n (x_i-\bar{x})\cdot (y_i-\bar{y}). \] \(S_{XY}\) es una medida simétrica (porque es igual a \(S_{YX}\)) y se puede leer como la suma de los productos de las desviaciones de \(X\) por las desviaciones de \(Y\) con respecto a sus respectivas medias. Fijémonos en la gráfica siguiente, donde se considera como centro el punto de coordenadas las medias aritméticas, \((\bar{x},\bar{y})\), que se llama centro de gravedad de la nube de puntos. Alrededor de él consideramos cuatro cuadrantes:
por primer cuadrante entendemos los puntos \((x_i,y_i)\) donde \(x_i > \bar{x}\) e \(y_i > \bar{y}\).
Por tercer cuadrante los puntos \((x_i,y_i)\) donde \(x_i < \bar{x}\) e \(y_i < \bar{y}\).
Por segundo cuadrante los puntos \((x_i,y_i)\) donde \(x_i > \bar{x}\) e \(y_i < \bar{y}\).
por cuarto cuadrante los puntos \((x_i,y_i)\) donde \(x_i < \bar{x}\) e \(y_i > \bar{y}\).
Si el signo de la desviación de \(X\) coincide con la de \(Y\), como ocurre en el primer y tercer cuadrante, se genera un sumando positivo en la fórmula de la covarianza; y cuando el signo es distinto -segundo y cuarto cuadrante- la aportación a la covarianza es negativa.
Entonces, en el primer y tercer cuadrante \((x_i-\bar{x})\cdot (y_i-\bar{y})\) siempre es un número mayor o igual a cero. En cambio, en el segundo y cuarto cuadrante, el producto \((x_i-\bar{x})\cdot (y_i-\bar{y})\) siempre es un número menor o igual a cero.
El punto de coordenadas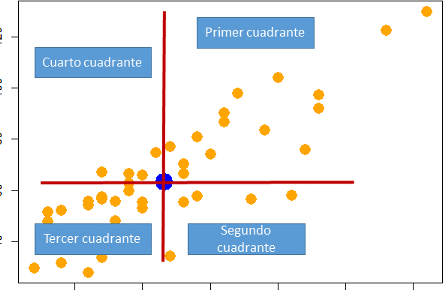
Figura 3.8: Cuadrantes relativos al centro de gravedad de la nube de puntos.
Por lo tanto, la concentración de valores en los distintos cuadrantes determina el signo y el valor de \(S_{XY}\). La covarianza mide, pues, la cantidad de relación lineal entre las variables y el sentido de esta, de la forma:
\(S_{XY}>0\), relación lineal positiva (si crece una variable,la otra también)
\(S_{XY}<0\), relación lineal negativa (si crece una variable,la otra decrece).
\(S_{XY}=0\), no hay relación lineal entre las variables.
De la simple observación de la nube de puntos podemos deducir que existe una relación lineal positiva entre las dos variables.
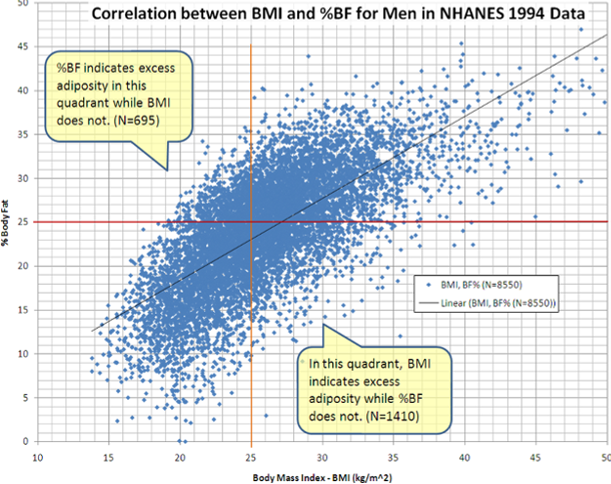
Figura 3.9: Ejemplo de diagrama de dispersión relacionando el índice de masa corporal y la grasa corporal.
Calculamos ahora la covarianza entre los dos conjuntos de datos anteriores.
data(Galton)
Gl<-data.frame(Galton)
cov(Gl$parent,Gl$child)## [1] 2.065data("water", package = "HSAUR")
mort<-data.frame(water)
cov(mort$hardness, mort$mortality)## [1] -4682Observamos que la covarianza en el primer conjunto de datos (Galton) es positiva (relación lineal creciente, puesto que ambas variables crecen en el mismo sentido), y en el segundo grupo de datos es decreciente (una variable crece, la otra decrece).
De todas formas, el número que resulte es de dificil interpretación, puesto que depende de las unidades en que vengan expresadas las variables. Es por ello que, en vez de trabajar con la covarianza, se trabaja con el llamado coeficiente de correlación lineal (o coeficiente de correlación lineal de Pearson).
3.5.3 Coeficiente de Correlación lineal (Pearson)
El coeficiente de correlación lineal o coeficiente de correlación de Pearson viene dado por \[\rho =r=\frac{S_{XY}}{S_X\cdot S_Y},\] y verifica
es una medida adimensional,
siempre toma valores en el intervalo \([-1,1]\) y
tiene el signo de \(S_{XY}\).
Veamos cuánto vale la correlación para cada uno de los conjuntos de datos anteriores:
data(Galton)
Gl<-data.frame(Galton)
cor(Gl$parent,Gl$child)## [1] 0.4588data("water", package = "HSAUR")
mort<-data.frame(water)
cor(mort$hardness, mort$mortality)## [1] -0.6548De manera general, tenemos:
cuando la relación lineal entre \(X\) e \(Y\) es exacta y directa, es decir, todos los puntos se encuentran sobre una recta con pendiente positiva, \(r\) vale 1.
cuando la relación lineal es exacta e inversa, es decir, todos los puntos se encuentran sobre una recta con pendiente negativa, r vale -1.
los valores intermedios (\(0<r<1\) o \(-1<r<0\)) darán lugar a que los puntos se aproximen más o menos a una recta que pasa por el medio de los mismos.
cuando no hay relación lineal, \(r\) vale 0.Este último caso se llama incorrelación, y se dice que las variables están incorreladas.
En la gráfica que sigue aparecen representados diferentes casos:
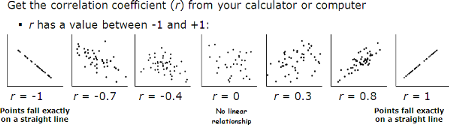
Figura 3.10: Posibles valores para el coeficiente de correlación.
El coeficiente de correlación lineal r también verifica que es invariante (salvo el signo) ante cambios de escala y origen, es decir, si construimos 2 nuevas variables \(Z=a+bX\), \(W=c+dY\), entonces: \(r_{(Z,W)}=r_{(X,Y)}\).
Tengamos en cuenta que la correlación mide la variación conjunta de las variables \(X\) e \(Y\). Si a una o a las dos variables les sumamos una constante, la variación conjunta entre las nuevas variables es la misma de antes. Si multiplicamos alguna (o las dos) por una constante, la variabilidad (varianza o desviación típica) se verá multiplicada por esa constante (salvo el signo).
Al cuadrado de \(r\) se le llama coeficiente de determinación, y se le denota por \(R^2\). Lógicamente, se verifica
\[0\leq R^2\leq 1,\]
y, cuánto más próximo esté \(R^2\) a 1, mayor es la relación lineal existente entre las variables, y menor cuanto más próximo esté \(R^2\) a cero. Muchas veces se multiplica esta medida por cien, y se habla entonces de un valor de \(R^2\) de, por ejemplo, el \(80\) por ciento, indicando la cantidad de relación lineal entre las variables. La relación lineal perfecta será, por lo tanto, del cien por cien. La relación será menor cuanto más se aproxime al cero por cien.
Calculemos la correlación en los dos conjuntos de datos usados anteriormente (Galton y water), y la elevamos al cuadrado para obtener el coeficiente de determinación:
data(Galton)
Gl<-data.frame(Galton)
cor(Gl$parent,Gl$child)^2## [1] 0.2105data("water", package = "HSAUR")
mort<-data.frame(water)
cor(mort$hardness, mort$mortality)^2## [1] 0.4288Así, podemos decir que la relación entre la altura de los hijos y la altura media de sus padres es lineal (positiva o creciente) en un \(21.04\) por ciento, y que la relación entre la mortalidad y la dureza del agua es lineal (negativa o decreciente) en un \(42.88\) por ciento.
Se concluye este apartado indicando que la independencia implica incorrelación, pero el recíproco no siempre es cierto (recordemos que la incorrelación se refiere a ausencia de relación lineal. Dos variables pueden estar relacionadas muy fuertemente mediante una función diferente a una lineal, y la incorrelación puede ser cero). Un ejemplo lo tenemos en la gráfica 3.11, donde las variables X e Y están relacionadas totalmente por una función matemática, pero si se calcula el valor de la correlación lineal da cero.
# 100 puntos desde -1 a 1
X=seq(-1,1,length=100)
# ecuación de una semi-circunferencia
Y=sqrt(1-X^2)
xy=data.frame(X,Y)
ggplot(data=xy, aes(x=X,y=Y))+
geom_point(color="darkorange", size=3) Figura 3.11: Correlación cero y relación matemática perfecta.
cor(X,Y)## [1] -3.162e-16Y en la gráfica 3.12 dibujamos otros dos ejemplos de sendos conjuntos de datos, en los que observamos que la correlación puede tomar valores muy próximos a cero y las nubes de puntos indican, en cambio, una fuerte relación entre las variables (y demostrar además que hay gente que no parece tener mucho qué hacer, pero, al menos, no se divierte haciendo maldades) (Matejka and Fitzmaurice 2017)
## [1] -0.06859## [1] -0.06447Figura 3.12: Correlación lineal cero para un donuts y un dinosaurio.
3.5.4 Ajuste y regresión bidimensional
Considerada una serie estadística \((x_1,y_1),…,(x_n,y_n)\), procedente de una distribución \((X,Y)\), el problema que se denomina ajuste de una nube de puntos o regresión bidimensional consiste en encontrar alguna relación que exprese los valores de una variable en función de los de la otra. La cuestión será elegir la mejor función, y determinar los parámetros (fórmula) de la misma. Esta relación podrá ser utilizada, posteriormente, para hacer predicciones aproximadas; por ejemplo, para hacer previsiones de ventas a corto o medio plazo, estimar el volumen de cosecha en función de la lluvia caída, la estatura de los hijos en función de la de los padres, etc…
La elección de esa función particular que mejor se adapte a las variables es el primer problema que habrá que solventar. En un principio, la observación de la nube de puntos puede dar una idea de la evolución de los valores de la variable dependiente (a partir de ahora \(Y\)) en función de los de la independiente (\(X\)).
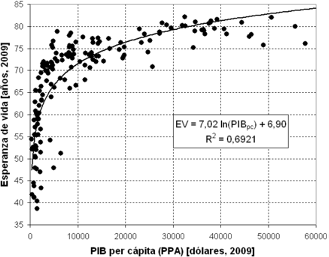
Figura 3.13: Ejemplo de una relación de tipo logarítmico entre variables.
Figura 3.14: Ejemplo de una relación de tipo exponencial.
A través del dibujo de la nube de puntos podemos, en muchas ocasiones, intuir que existirán mejores funciones que la línea recta (que es la más sencilla de todas) para explicar la variable Y en función de la variable X. El proceso de elegir la mejor función no tiene por qué ser sencillo ni simple. Debemos tener también en cuenta que quizá no haya una única variable \(X\) influyendo en la variable \(Y\), sino que pueden existir diferentes variables explicativas \(X_1\),\(X_2\),…,\(X_k\) que sean necesarias para poder establecer predicciones de la variable Y de interés.
3.5.5 El caso lineal
Como hemos visto en los ejemplos utilizados antes, observando el dibujo de la nube de puntos, tendremos que existe una relación de tipo lineal entre las variables si los puntos “forman” alguna disposición que se pueda concentrar alrededor de una línea recta (Figura 3.15: relación lineal decreciente).
Figura 3.15: Datos relacionando dureza del agua y mortalidad.
Matemáticamente, la variable \(Y\) puede expresarse en función de \(X\) como una línea recta a través de una función del tipo \[Y=a+bX\] Esta recta se llama recta de regresión, y sirve para predecir el valor de \(Y\) para un valor nuevo de la variable \(X\).
La forma de calcular los mejores valores para \(a\) y \(b\) (es decir, aquellos valores que consigan que la recta se “aproxime” lo más posible a los datos y, por consiguiente, luego permita obtener mejores predicciones) se llama método de los mínimos cuadrados (ver el capítulo de probabilidades si se tiene interés por el desarrollo histórico de este método).
Los valores de los parámetros \(a\) y \(b\), utilizando este método, se obtienen en función de los datos como: \[b=\frac{S_{XY}}{S_X^2}\] \[a=\bar{y}-b\bar{x}\].
Figura 3.16: Línea de regresión para los datos del ejemplo anterior.
##
## Call:
## lm(formula = mortality ~ hardness, data = mort)
##
## Coefficients:
## (Intercept) hardness
## 1676.36 -3.23Si ahora quisiéramos utilizar la recta para hacer alguna predicción, escribiríamos \(a\) = 1676.356 y \(b\)=-3.226 y calcularíamos \(y=a+bx\).
La predicción usando una recta de regresión tiene claros problemas. Uno es el de la extrapolación (salirnos de los límites del rango de valores analizado). Un ejemplo clásico es el de los récords de los cien metros.
Como sabemos, la marca mundial de los 100 metros lisos ha ido disminuyendo con el paso de los años. Si calculamos la recta de regresión que relacione \(X\)=“año” e \(Y\)=“tiempo récord para recorrer los 100 metros”, podríamos predecir cual sería el año en que se llegaría a un tiempo de 0 segundos, o incluso un tiempo negativo.
record_100_m <- read_excel("Data/record-100-m.xlsx")
dt=data.frame(x=record_100_m[,1], y=record_100_m[,2])
names(dt)<-c("año", "record")
p<- ggplot(data=dt,
aes(x=año,y=record),color="red",size=3)+
geom_point(color="red",size=3)+
geom_smooth(method = "lm",se=FALSE)
ggplotly(p)Figura 3.17: Tiempo realizado frente al año de la carrera, junto con la recta de mínimos cuadrados.
El valor que se obtiene para \(R^2\) con estos datos es 0.9484.
Es evidente que este tipo de previsiones no tiene sentido, puesto que los valores mínimos de Y para los años actuales parece muy difícil rebajarlos. En Internet pueden encontrarse estudios de cuál es la función más adecuada para el ajuste de estas variables, con el fin de obtener una posible predicción dentro de límites razonables.
A veces una variable depende de otra, pero no a la inversa. Por ejemplo, un descenso de temperatura puede influir en un aumento del consumo eléctrico (por las estufas), pero un aumento del consumo eléctrico no influirá en el descenso de temperatura. De hecho, el aumento del consumo eléctrico podrá relacionarse tanto con un descenso de temperatura como con un aumento (si hace más calor, aumentará el uso del aire acondicionado).
3.5.6 El origen del término “regresión”
Fue Francis Galton el creador de este término. Su fama histórica procede, entre otras cosas, por ser el creador de la psicología diferencial, del mapa del tiempo, del saco de dormir, del silbato para perros, ser pionero en la clasificación de huellas dactilares, y por la creación del término “eugenesia”.En 1884 fundó el primer laboratorio de Biometría, y calculó que la probabilidad de que haya dos huellas dactilares iguales es practicamente nula.

Figura 3.18: Francis Galton y una de sus muchas frases célebres.
3.5.6.1 Galton y la eugenesia
La selección artificial de seres humanos fue sugerida desde muy antiguo, al menos desde Platón, quien creía que la reproducción humana debía ser controlada por el gobierno. Platón registró estos puntos de vista en La República: «que los mejores cohabiten con las mejores tantas veces como sea posible y los peores con las peores al contrario». Platón proponía que el proceso se ocultase al público mediante una especie de lotería. Otros ejemplos antiguos incluyen la supuesta práctica de las polis de Esparta de abandonar a los bebés fuera de los límites de la ciudad durante un periodo de tiempo, considerándose más fuertes a los supervivientes.
Durante los años 1860 y 1870, Galton sistematizó estas ideas y costumbres de acuerdo al nuevo conocimiento sobre la evolución del hombre y los animales provisto por la teoría de su primo Charles Darwin. Tras leer El origen de las especies, Galton observó una interpretación de la obra de Darwin a través de la cual los mecanismos de la selección natural eran potencialmente frustrados por la civilización humana. Galton razonó que, dado que muchas sociedades humanas buscaban proteger a los desfavorecidos y los débiles, dichas sociedades estaban reñidas con la selección natural responsable de la extinción de los más débiles.
Galton esbozó por vez primera su teoría en el artículo de 1865 Talento y personalidad hereditarios, explicándola luego más detalladamente en su libro de 1869 El genio hereditario. Galton comenzó estudiando la forma en la que los rasgos humanos intelectuales, morales y de personalidad tendían a presentarse en las familias. Su argumento básico era que el «genio» y el «talento» eran rasgos hereditarios en los humanos (aunque ni él ni Darwin tenían aún un modelo de trabajo para este tipo de herencia). Galton concluyó que, puesto que puede usarse la selección artificial para exagerar rasgos en otros animales, podían esperarse resultados similares al aplicar estas prácticas en humanos. Como escribió en la introducción de El genio hereditario:
“Me propongo mostrar en este libro que las habilidades naturales del hombre se derivan de la herencia, bajo exactamente las mismas limitaciones en que lo son las características físicas de todo el mundo orgánico. Consecuentemente, como es fácil, a pesar de estas limitaciones, lograr mediante la cuidadosa selección una raza permanente de perros o caballos dotada de especiales facultades para correr o hacer cualquier otra cosa, de la misma forma sería bastante factible producir una raza de hombre altamente dotada, mediante matrimonios sensatos durante varias generaciones consecutivas.”
Según Galton, la sociedad ya fomentaba las enfermedades disgenéticas, afirmando que los menos inteligentes se reproducían más que los más inteligentes. Galton no propuso sistema de selección alguno, sino que esperaba que se hallaría una solución cambiando las buenas costumbres sociales de forma que animasen a la gente a ver la importancia de la reproducción.
Galton usó por primera vez la palabra eugenesia en su libro de 1883 Investigaciones sobre las facultades humanas y su desarrollo (Inquiries into Human Faculty and Its Development), en el que quiso “mencionar los diversos tópicos más o menos relacionados con el cultivo de la raza o, como podríamos llamarlo, con las cuestiones eugenésicas”. En 1904, Galton aclaró su definición de eugenesia como “la ciencia que trata sobre todas las influencias que mejoran las cualidades innatas de una raza, y también con aquellas que las desarrollan hasta la mayor ventaja”.
La formulación de Galton de la eugenesia estaba basada en un fuerte enfoque estadístico, fuertemente influenciado por la “física social” de Adolphe Quetelet. Sin embargo, a diferencia de éste, Galton no exaltaba al “hombre medio”“, sino que lo despreciaba por mediocre. Galton y su heredero estadístico Karl Pearson desarrollaron lo que se llamó el enfoque biométrico de la eugenesia, que desarrolló nuevos y complejos modelos estadísticos (más tarde exportados a campos completamente diferentes) para describir la herencia de los rasgos.
La eugenesia terminó aludiendo a la reproducción humana selectiva como intento de obtener niños con rasgos deseables, generalmente mediante el enfoque de influir sobre las tasas de natalidad diferenciales. Estas políticas se clasificaban en su mayoría en dos categorías: eugenesia positiva, la mayor reproducción de los que se consideraba que contaban con rasgos hereditarios ventajosos, y la eugenesia negativa, la disuasión de la reproducción de los que tenían rasgos hereditarios considerados malos. En el pasado, las políticas eugenésicas negativas han ido de intentos de segregación a esterilizaciones e incluso genocidio. Las políticas eugenésicas positivas han tomado típicamente la forma de premios o bonificaciones para los padres “aptos”" que tenían otro hijo.
El ejemplo que motivo a Galton: la altura de los padres correlaciona linealmente con la estatura de los hijos (Figura 3.19), pero la estatura de los hijos tiende a la media. Es decir, el hijo de unos padres muy altos es muy probable que sea más bajo que ellos. Significa que existe una regresión a la media, o lo que Galton llamó regresión hacia la mediocridad.
data(Galton)
Gl<-data.frame(Galton)
# dibujo de los datos y la línea de regresión
xyplot(child ~ parent, type = c("p", "r"),data = Gl) Figura 3.19: Recta de regresión de la estatura de los hijos en función de la media de los padres.
# cálculo de los coeficientes de la recta
linea<-lm(child~ parent,data = Gl)
linea##
## Call:
## lm(formula = child ~ parent, data = Gl)
##
## Coefficients:
## (Intercept) parent
## 23.942 0.646En el dibujo original que hizo en su día Galton (Figura 3.20), la línea de regresión o de mínimos cuadrados aparece comparada con la diagonal del gráfico (sería la recta \(Y=X\)). De esta manera se puede comprender perfectamente la regresión hacia la media. A partir del centro de gravedad, la línea de regresión está más baja que la diagonal, lo que significa que, en media, los valores altos de la \(Y\) “descienden” o “regresan” hacia la media. Si no existiera esa regresión, el crecimiento sería continuo de generación en generación (se iría creciendo continuadamente).
knitr::include_graphics('Figure/Galton-height-regress.jpg')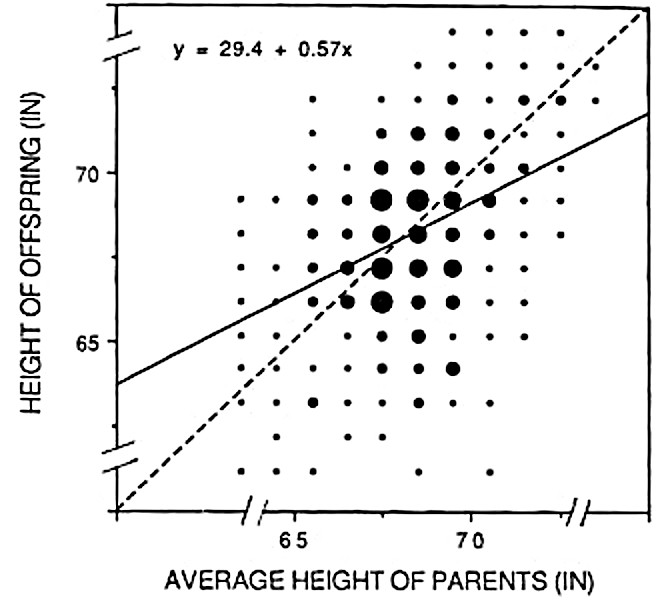
Figura 3.20: Gráfico original de Galton.
Pero no sólo la estatura es una característica, por así decirlo heredable, es decir que parte de la altura de una persona depende de la de sus padres. Otras características, como la inteligencia, la valentía, la capacidad de progresar en una asignatura, o en un deporte, presentan propiedades similares. Observemos:
Familias de genios: https://hipertextual.com/2018/03/nobel-padres-hijos
Un caso particular en matemáticas: los Bernoulli
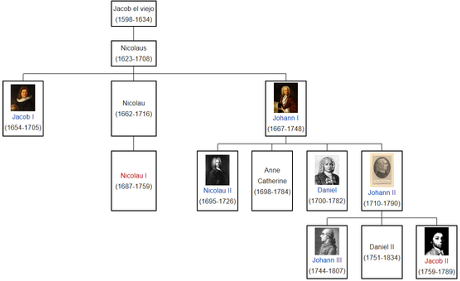
Figura 3.21: Los Bernoulli, una familia de genios de la ciencia. Aquí en España tenemos a los Pelayo y a los del Río (no son primos míos, ojo) .

Figura 3.22: Dakota Johnson (50 sombras de Grey), hija de Melanie Griffith y Don Johnson, famosos actores de los años 80.
Fijémonos ahora en otra hija de Melanie Griffith (de su matrimonio con Antonio Banderas). Además, mucha gente joven no sabe que su abuela (la madre de Melanie) fue la actriz protagonista de Los Pajaros.

Figura 3.23: Otra hija de Melanie Griffith (de su matrimonio con Antonio Banderas). Además, mucha gente desconoce que su abuela (la madre de Melanie) fue la actriz protagonista de Los Pajaros.
3.5.6.2 La importancia de la regresión a la media en entornos educativos
El premio nobel de economía Daniel Kahneman, en su libro Pensar rápido, pensar despacio (Daniel Kahneman and Egan 2011), expone:
“La regresión a la media se da en todas las circunstancias donde se dan medidas extremas y tiene consecuencias predictivas de mucho interés, por ejemplo en los rendimientos escolares, deportivos o en cualquier otra situación donde los resultados pueden cuantificarse. Por ejemplo, si en un primer examen un niño saca un 10 y otro saca un 2, siendo la nota media de la clase un 5, es bastante posible que en un segundo examen el que sacó un 10 disminuya su nota mientras que el que sacó un 2 la aumente, pues las puntuaciones tienden a igualarse buscando la media.
Pero lo más interesante de esta cuestión es que esta regresión va a darse igual, tanto si animamos o reprendemos al suspendido como si nos dedicamos a lisonjear al sobresaliente. Algo que va en contra de nuestras intuiciones pedagógicas. En ellas tendemos a “echar la bronca” a los que quedan por debajo de la media y a alabar los buenos rendimientos de los que se salen por arriba, sin caer en la cuenta de que nuestros esfuerzos no sirven de nada cuando estamos enfrentando puntuaciones extremas. Lo cual no quiere decir que la motivación, el apoyo o el empoderamiento no sean buenas estrategias pedagógicas, sino que solo sirven en las medianías y no en los casos extremos.
Y como tenemos tendencia a premiar a los buenos y a castigar a los malos, estamos condenados a cosechar decepciones por parte de los buenos (y con los que somos mas agradables) y sorpresas agradables con aquellos con los que somos desagradables.”
Kahneman expone estas conclusiones en su libro, explicando a su vez una experiencia vivida durante una etapa de colaboración con pilotos de aviones del ejercito israelí, comprobando que las felicitaciones tras un buen vuelo (refuerzo positivo) se revelaban como mejor estrategia en contra de una reconvención (refuerzo negativo), puesto que durante una serie de entrenamientos, todos los pilotos tienden a hacer unos ejercicios mejores que otros, por el efecto de regresión a la media.
3.5.6.3 Correlación espuria
Algunos ejemplos tomados de la literatura estadística (resumidos en la wikipedia) dan idea de errores comunes y detalles que cualquier investigador debe considerar siempre que relacione dos variables. Los siguientes son ejemplos de conclusiones erróneas obtenidas de una mala interpretación de la correlación entre dos variables (llamada correlación espuria).
- Dormir sin quitarse los zapatos tiene una alta correlación con despertarse con dolor de cabeza. Por lo tanto, el dormir con los zapatos puestos ocasiona levantarse con dolor de cabeza.
Este resultado mezcla los conceptos de correlación y causalidad, porque concluye que dormir con los zapatos puestos provoca dolor de cabeza al levantarse. Hay un tercer factor que no se ha tenido en cuenta, que es que irse borracho a la cama provoca ambos efectos: no poder ni quitarse los zapatos y levantarse mareado.
Los niños pequeños que duermen con la luz encendida son mucho más propensos a desarrollar miopía en la edad adulta. Esta fue la conclusión de un estudio de la Universidad de Pennsylvania, publicado en 1999 en la revista Nature. Un estudio posterior de la Ohio State University refutó esta teoría, y encontró una fuerte relación entre la miopía de los padres y el desarrollo de la miopía infantil, advirtiendo que los padres miopes tenían más probabilidades de dejar una luz encendida en el dormitorio de sus hijos. De nuevo una tercera variable no tenida en cuenta (la miopia de los padres), causaba la alta correlación entre las otras dos variables relacionadas.
Cuando aumentan las ventas de helado, la tasa de muertes por ahogamiento también aumenta. Por lo tanto, el consumo de helado provoca ahogamiento. El helado se vende durante los meses de verano a un ritmo mucho mayor que en épocas más frías, y es durante estos meses de verano que las personas son más propensas a participar en actividades relacionadas con el agua, como la natación. El mayor porcentaje de muertes por ahogamiento es causado por una mayor exposición a las actividades acuáticas.
Desde 1950, tanto el nivel de dióxido de carbono (CO2) en la atmósfera como los niveles de obesidad han aumentado considerablemente. Por lo tanto, el CO2 atmosférico provoca la obesidad. Obviamente, en las ciudades que han mejorado su nivel de vida a partir de los años 50, se come más y se expulsa más CO2 a la atmósfera (coches, fábricas… ).
Con una disminución en el uso de sombreros, ha habido un aumento en el calentamiento global durante el mismo período. Por lo tanto, el calentamiento global es causado por personas que abandonan la práctica de usar sombreros. La explicación de este efecto sería muy parecida a la del ejemplo anterior.
Por último, en este video, quien quiera puede ver con detalle un curioso estudio que se publicó en \(2012\) en la prestigiosa revista New England Journal of Medicine, en donde el autor estudió la correlación entre los premios nobel de los países y el consumo de chocolate (sí, el de comer) en los mismos.
Los datos por sí alguien los quiere: DatosPN
- Y aquí una página donde se pueden encontrar montones de gráficos con correlación espuria:
References
Hand, D.J., F. Daly, K. McConway, D. Lunn, and E. Ostrowski. 1993. A Handbook of Small Data Sets. A Handbook of Small Data Sets, v. 1. Taylor & Francis.
Kahneman, Daniel, and Patrick Egan. 2011. Thinking, Fast and Slow. Vol. 1. Farrar, Straus; Giroux New York.
Matejka, Justin, and George Fitzmaurice. 2017. “Same Stats, Different Graphs: Generating Datasets with Varied Appearance and Identical Statistics Through Simulated Annealing.” In Proceedings of the 2017 Chi Conference on Human Factors in Computing Systems, 1290–4. CHI ’17. New York, NY, USA: ACM. doi:10.1145/3025453.3025912.