4.12 Probabilidad condicionada

En la incertidumbre asociada a los experimentos aleatorios puede existir un cierto dinamismo, ya que la información adicional que vayamos obteniendo sobre un proceso puede modificar las probabilidades de los sucesos.

Harry el sucio

En este fragmento de la película “Harry el sucio” (1971), comprobamos como la intuición inicial del alcalde de San Francisco (John Vernon), de que Harry Callahan (Clint Eastwood) se había excedido en el uso de la fuerza (matar a un sospechoso de intento de violación) cambia, a medida que el policía va dando pruebas acerca de las intenciones del sospechoso. Es un ejemplo de modificación de la probabilidad de un suceso (ser culpable, en este caso) a medida que se tienen nuevas evidencias. La forma de medir y evaluar las probabilidades bajo este esquema se conoce como evaluación de la probabilidad condicionada.

Retomemos este ejemplo donde considerábamos la clasificación de hombres y mujeres en función de padecer o no artrosis:

Artrosis No Artrosis Totales
Hombres 45 30 75
Mujeres 55 15 70
Totales 100 45 145

Entra en la consulta una mujer. ¿Cuál es la probabilidad de que tenga artrosis?

Esto se escribe \(P(A\mid M)\) y se calcula como siempre, como casos favorables entre posibles (55 mujeres con artrosis, entre 70 mujeres). \[P(A\mid M)=55/70\]

A partir de la tabla, podemos ver que la probabilidad del suceso intersección es \[P(A\cap M)=55/145\]

y que la probabilidad de ser mujer \[P(M)=55/145\] Se ve rápidamente la relación: \[P(A\mid M)=\frac{P(A\cap M)}{P(M)}\] En general, la probabilidad de un suceso \(A\) condicionado a otro suceso \(B\) es

\[P(A\mid B)=\frac{P(A\cap B)}{P(B)},\]

donde se supone que la probabilidad del suceso \(B\) no puede ser cero.

De esta definición se deduce la forma general de calcular la probabilidad de una intersección:

\[P(A\cap B)= P(A)\cdot P(B\mid A)=P(B)\cdot P(A\mid B)\]

Ejercicio 4.1 De 1000 mujeres mayores de 40 años que acudieron a un centro de salud, se realizó la siguiente tabla para el estudio de la relación entre la presencia o no de osteoporosis y haber tenido la menopausia:

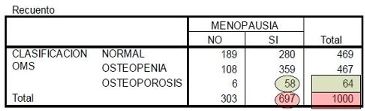
Tabla de contingencia menopausia - osteoporosis.

Figura 4.22: Tabla de contingencia menopausia - osteoporosis.

La probabilidad de tener osteoporosis es \(64/1000=0.064.\)

Ahora bien, es conocido que la probabilidad de tener osteoporosis es mayor si se ha tenido la menopausia. Entonces podríamos calcular \[P(Osteoporosis\mid Menopausia)=58/697=0.098\] Si calculamos en cambio la probabilidad de Haber tenido la Menopausia condicionado a Tener osteoporosis: \[P(Menopausia\mid Osteoporosis)=58/64\] Comprobamos lo que sucede de manera general: \(P(A\mid B)\) no coincide con \(P(B\mid A)\).

Aunque a veces pueda ser fácil liarse. Veamos otro ejemplo:

Ejercicio 4.2 Un médico observa que el 30% de sus pacientes son mujeres y que el 40% de sus pacientes fuma. De los fumadores, el 75% son hombres. Calcular el porcentaje de mujeres que fuman entre los pacientes del doctor, y el porcentaje de fumadoras entre las mujeres.

Solución:

Primero; en caso de duda, diagrama de Venn:

Diagrama de venn Fumadores (1)

Figura 4.23: Diagrama de venn Fumadores (1)

Nos piden, primero, porcentaje de mujeres que fuman: \(P(M\cap F)\)

Lo que nos piden es el área representada por el rectángulo verde (mujeres y a la vez fumadores)

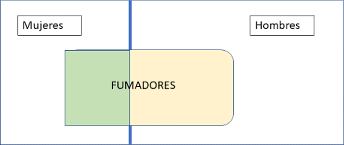
Diagrama de venn Fumadores (2)

Figura 4.24: Diagrama de venn Fumadores (2)

Ahora \[P(M\cap F)= P(F)\cdot P(M\mid F)= 0.4\cdot (1-0.75)=0.4\cdot 0.25= 0.1,\] es decir el 10 por ciento.

El porcentaje de fumadoras entre las mujeres será el mismo rectángulo, pero considerado sólo en el grupo de mujeres.

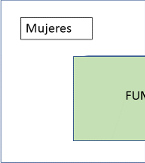
Diagrama de venn Fumadores (3)

Figura 4.25: Diagrama de venn Fumadores (3)

\[P(F\mid M)=\frac{P(F\cap M)}{P(M)}=\frac{0.1}{0.3}=0.33.\]

Vemos que la probabilidad condicionada y la probabilidad de la intersección no son lo mismo.

Por otro lado, \[P(F\mid M) \neq P(M\mid F)\]

La primera probabilidad nos da el porcentaje de mujeres que fuman (en el grupo de mujeres como TOTAL) y la segunda nos da el porcentaje de mujeres que hay en el grupo de fumadores, y sería:

\[P(M\mid F)=\frac{P(M\cap F)}{P(F)}=\frac{0.1}{0.4}=0.25.\]

Puede demostrarse que la probabilidad condicionada cumple todas las propiedades vistas de la probabilidad. Esto es, si \(E\) es cualquier suceso con probabilidad mayor que cero:

  • \(P(\bar{A}\mid E)= 1-P(A\mid E)\)

  • \(P(A\cup B \mid E)= P(A\mid E) + P(B \mid E) - P(A\cap B \mid E)\)

  • Si \(A\subset B\), entonces \(P(A\mid E)\leq P(B\mid E)\)

  • \(P((A-B)\mid E)=P(A\mid E)-P((A \cap B)\mid E)\)

Ejercicio 4.3 En las bodas de Caná, el 70% de los presentes eran mujeres. De ellas el 10% eran católicas. De los hombres, eran católicos el 20%. a) ¿Qué porcentaje de católicos había? b) Se elije a una persona al azar y es católica. ¿Cuál es la probabilidad de que sea un hombre?

Solución:

Con los datos, creamos una tabla de doble entrada:
Católicos No Católicos Totales
Hombres \(0.2 \cdot 0.3\)
Mujeres \(0.7 \cdot 0.10\) \(0.7\)
Totales \(1\)

Rellenamos los huecos:

Católicos No Católicos Totales
Hombres \(0.2 \cdot 0.3\) \(0.24\) \(0.3\)
Mujeres \(0.7 \cdot 0.10\) \(0.63\) \(0.7\)
Totales \(0.13\) \(0.87\) \(1\)

Mirando a la tabla respondemos

  1. \(P(C)=0.13\)
  2. \(P(H\mid C)=P(H\cap C)/P(C)\) y estas son \(0.06/0.13=0.46\)