4.8 Definiciones básicas
Para introducir detalladamente la noción de probabilidad, vamos a hablar de dos tipos de experimentos. Consideraremos que un experimento es un proceso por medio del cual se obtiene una observación. Bajo este enfoque, podemos distinguir entre experimentos deterministas y aleatorios.
Los primeros son aquellos que siempre que se repitan bajo condiciones análogas llevan al mismo resultado, por tanto este resultado puede predecirse.
Por el contrario, un experimento aleatorio es el que puede dar lugar a varios resultados conocidos previamente, sin que sea posible saber de antemano cuál de ellos se va a producir.
### Espacio muestral El conjunto de los posibles resultados de un experimento aleatorio se llama espacio muestral. Se representa con la letra griega \(\Omega\).
4.8.1 Suceso elemental.
Se llama suceso elemental a cada uno de los posibles resultados de un experimento aleatorio. En el ejemplo del lanzamiento de un dado, cualquiera de los números del 1 al 6 es un suceso elemental.
4.8.2 Suceso.
Es un subconjunto del espacio muestral, \(A\subset \Omega\). Se dice que ocurre un suceso si ocurre alguno de los sucesos elementales que lo componen.
salir número par={2,4,6}.
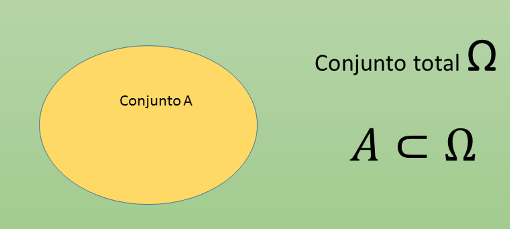
Figura 4.7: Representación de un suceso contenido en un espacio muestral.
4.8.3 Diagramas de Venn
Son las representaciones gráficas (habitualmente con círculos) de sucesos, y las posibles operaciones o relaciones entre ellos. Nos van a resultar muy útiles para entender las propiedades de las probabilidades de los sucesos.
Se dice de John Venn (lógico matemático, 1834-1923) que fue quién inventó la noción de frecuencia.
“La probabilidad de un suceso es su frecuencia relativa dentro de la serie” (La lógica del azar; 1866)
4.8.4 Suceso imposible.
Es el suceso que no puede ocurrir nunca. Como conjunto, es el conjunto vacío \(\varnothing\).
4.8.5 Unión de sucesos
La Unión (de conjuntos o sucesos) \(A\cup B\) es el conjunto o suceso formado por los elementos que están en \(A\) o están en \(B\).
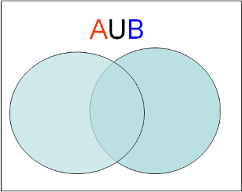
Figura 4.8: Diagrama de Venn de la unión de conjuntos.
tener un hueso roto, y el suceso \(B\) estar resfriado. El suceso \(A\cup B\) consiste en que el enfermo puede tener un hueso roto, o estar resfriado, o tener ambas cosas a la vez.
Se puede generalizar a varios sucesos: \(A_1\) tener la enfermedad \(1\), \(A_2\) tener la enfermedad \(2\) y \(A_2\) tener la enfermedad \(n\). El suceso unión \(A_1\cup A_2 \cup ... \cup A_n\) sería tener una, dos, o varias enfermedades simultaneamente (pudiendo tenerlas todas).
4.8.6 Intersección de sucesos
\(A\cap B\) está formado por los elementos que están simultáneamente en \(A\) y en \(B\).
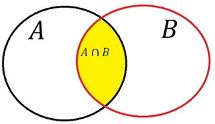
Figura 4.9: Suceso A: doble grado en español y gallego. Suceso B: doble grado en inglés y español. Intersección: grado en español.
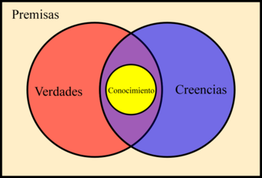
Figura 4.10: “La ciencia es un juicio verdadero acompañado de razón”, Platón.
4.8.7 Sucesos incompatibles
Dos sucesos se dicen incompatibles si no pueden ocurrir simultaneamente (al lanzar un dado no puede salir un número par e impar a la vez). Dos sucesos son incompatibles si como conjuntos son disjuntos (\(A\cap B=\varnothing)\) (esta definición se extiende a más de dos sucesos o conjuntos).

Figura 4.11: Algunos ejemplos de sucesos incompatibles.
Veamos ahora el concepto de “incompatibles” explicado por nada menos que el abogado (uno de ellos) de la infanta Cristina, cuando presentó como estrategia que la infanta no sabía nada de los negocios de su marido porque, al estar enamorada de él, confiaba en él ciegamente.
4.8.8 Diferencia de sucesos
\(A- B\) está formado por los elementos de \(A\) que no están en \(B\).
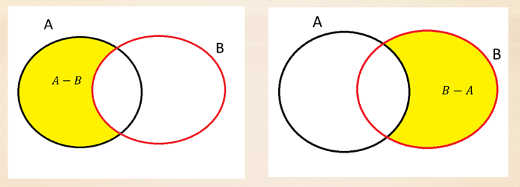
Figura 4.12: Diferencia de sucesos.
tener un hueso roto, y \(B\) estar resfriado, \(A-B\) es tener un hueso roto y NO estar resfriado. \(B-A\) sería estar resfriado Y no tener un hueso roto.
Supongamos que buscamos en Google información sobre el nuevo modelo de telefóno móvil de Chamchung: el Chamchung-Boom2. Una busqueda genérica podría ser escribir: Chamchung-Boom2 a secas.
Si queremos garantizar que salga información sobre el precio pondríamos Chamchung-Boom2 +precio que sería equivalente a la intersección de Chamchung-Boom2 y precio.
Si escribimos Chamchung Boom2 - Ifone le estamos indicando a Google que no aparezca en los resultados la palabra Ifone, puesto que muchos resultados van a ofrecer comparativas con el Ifone, y puede que eso no nos interese. Esto valdría como ejemplo de diferencia de sucesos.
4.8.9 Complementario de un suceso
El complementario de un suceso \(A\) se escribe \(A^{c}\) o \(\overline{A}.\) Corresponde al suceso formado por todos los elementos del espacio total \(\Omega\) que no están en \(A.\)
Se verifica que \(A\cap \overline{A}= \varnothing\) y \(A\cup \overline{A}= \Omega.\)
que salga un número par, el suceso \(B\) es que salga número impar.
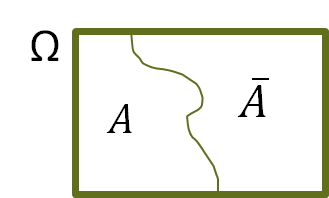
Figura 4.13: Suceso complementario.
Pequeño resumen:
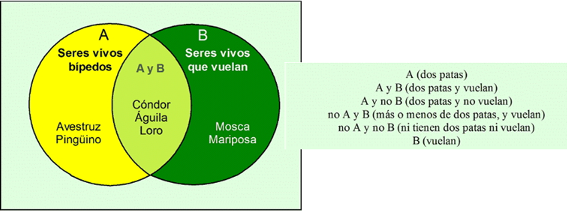
Figura 4.14: Diagrama de Venn con animales.
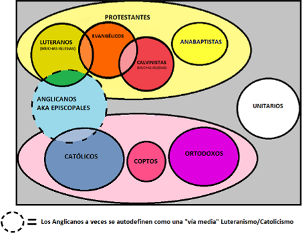
Figura 4.15: Diagrama de Venn de familias Cristianas.
Para hacernos una idea de que los diagramas de Venn constituyen una herramienta muy utilizada, veamos un trozo de una película donde los citan (americana, lo cual significa que para ellos el uso de este tipo de diagramas es algo muy común). La escena pertenece a “The Town (2010)”.

Figura 4.16: A algunos es muy difícil ponerlos de acuerdo hasta con un diagrama de Venn.
Y más ejemplos:
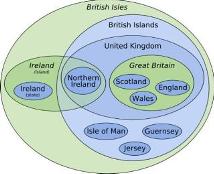
Figura 4.17: Para entender bien como se componen las islas británicas.
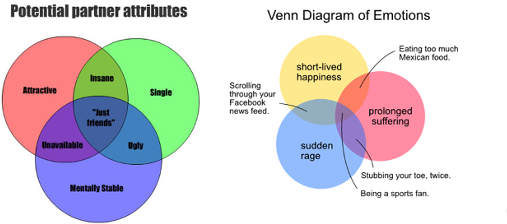
Figura 4.18: Venga, más…