4.15 Teorema de la probabilidad total (Laplace)

Sean los sucesos \(A_1,A_2,\ldots,A_n\) una partición del espacio muestral \(\Omega\), y sea \(B\) un suceso cualquiera.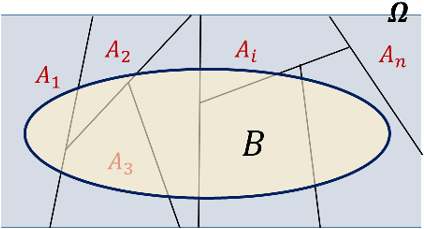

Figura 4.30: Partición: sucesos disjuntos que recubren el total.

Se cumple que la probabilidad del suceso \(B\) puede expresarse en función de los sucesos \(A_i\) de la siguiente manera (fórmula de la probabilidad total): \[ P(B)=P(B \mid A_1)\cdot P(A_1) + P(B \mid A_2)\cdot P(A_2) + \cdots + P(B \mid A_n)\cdot P(A_n) \]

Ejemplo 4.1 La tienda online favorita del 33 por ciento de los socios de un foro es Pccomponendas, un 8 por ciento prefiere Medianamart, el 2 por ciento prefiere Evoy y el resto prefieren comprar en Amazonas. La probabilidad de que el pedido se pierda y no llegue al destinatario, según la casa que lo envíe, es 0.8, 0.9, 0.7 y 0.6 respectivamente. Pepe, forero del 2003, ha pedido el último modelo de linterna. Si acaba de entrar al foro y el primer hilo que abre ya es para insultar, ¿crees que está cabreado porque no ha recibido el envío?

Solución

Definimos los sucesos: \(A_1\)=“pedido a Pccomponendas”,

\(A_2\)=”pedido a Medianamart”,

\(A_3\)=”pedido a Evoy” ,

\(A_4\)=”pedido a Amazonas”,

y \(B\)=“el pedido no llega a tiempo”.

Se tiene que

\(P(A_1)=0.33,P(A_2)=0.08,P(A_3)=0.02,P(A_4)=0.57.\)

Como vemos, los sucesos \(A_1, A_2,A_3\) y \(A_4\) son incompatibles y sus probabilidades suman 1, por lo que cumplen las hipótesis del teorema de las probabilidades totales.

Nos dicen, además, que \(P(B\mid A_1)=0.8, P(B\mid A_2)=0.9, P(B\mid A_3)=0.7, P(B\mid A_4)=0.6.\)

Por el teorema de las probabilidades totales, la probabilidad de que el pedido no se ha recibido es \(P(B)=\) \[P(B\mid A_1)\cdot P(A_1)+P(B\mid A_2)\cdot P(A_2)+P(B\mid A_3)\cdot P(A_3)+P(B\mid A_4)\cdot P(A_4)=\] \[=0.8\cdot 0.33+0.9\cdot 0.08+0.7\cdot 0.02+0.6\cdot 0.57=0.692.\] Vemos que la probabilidad de que Pepe no haya recibido el envío es más alta qué la probabilidad de que sí lo haya recibido, por lo tanto comprendemos su enfado.

Ejemplo 4.2 Otro ejemplo del canal de youtube de fonemato: