7.5 I.C. para la media de una población normal con varianza conocida

El objetivo es construir un intervalo de confianza para la media \(\mu\) de una población normal (altura media, peso medio, tiempo medio haciendo gimnasia…)

Por una vez, y sin que sirva de precedente, vamos a ver cómo es la construcción matemática del intervalo de confianza. Consideremos la variable \(X\in N(\mu,\sigma)\), que representa a la característica que estamos midiendo (altura, peso…). Supongamos que \(\sigma\) es conocida.

Consideramos una muestra aleatoria simple \(X_1,\ldots,X_n\) de la variable \(X\). Dado el nivel de confianza \(1-\alpha\), elegimos el llamado estadístico pivote \[ T=\frac{\bar{X}-\mu }{\sigma /\sqrt{n}}. \]

Un estadístico es una función de variables aleatorias y es también otra variable aleatoria. En este caso, vamos a ver que distribución sigue esta variable \(T\) que acabamos de definir (el término pivote es una nomenclatura utilizada en los test de hipótesis).

Como vimos anteriormente, la media muestral verifica \[ \bar{X} \in N\left(\mu, \dfrac{\sigma }{ \sqrt{n}}\right). \] Por lo tanto, si tipificamos la variable (restamos la media y dividimos por la desviación típica), obtenemos la variable \(T\), lo que quiere decir que esta variable sigue una distribución normal estándar (\(N(0,1)\)).

Teniendo en cuenta que \(\frac{\alpha}{2} =P(Z\geq z_{\alpha/2})\) (Figura 7.10), sabemos que

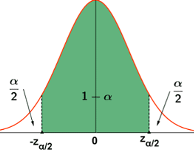
Figura 7.10: Niveles de significación en una normal estandarizada

\[ 1-\alpha=P\left( -z_{\alpha /2}<\frac{\bar{X}-\mu }{\sigma /\sqrt{n} }< z_{\alpha /2}\right) \]

Despejando el parámetro \(\mu\) obtenemos \[ 1-\alpha=P\left( \bar{X}- z_{\alpha /2}\frac{\sigma }{\sqrt{n}}<\mu <\bar{X}+ z_{\alpha /2}\frac{\sigma }{\sqrt{n}}\right) \] Por tanto, el I.C. para \(\mu\) al nivel de confianza \(1-\alpha\)} es \[ (L,U)=\left(\bar{X}-z_{\alpha /2}\frac{\sigma }{\sqrt{n}},\bar{ X}+\text{ } z_{\alpha /2}\frac{\sigma }{\sqrt{n}}\right) \]

El procedimiento teórico para llegar a esta fórmula es simple, aunque difícil de seguir para cualquiera con pocos conocimientos matemáticos. En todo caso, lo importante es que la fórmula del intervalo no tiene excesiva dificultad. El intervalo está centrado en el estimador media muestral, y los extremos consisten en restar y sumar la misma cantidad: un valor que depende del nivel de confianza utilizado, multiplicado por el error muestral de la media.

*Retomamos el Ejercicio anterior.**

En una clínica de fisioterapia se quiere saber el número de grados que acaba doblando una rodilla después de dos semanas de tratamiento. Las medidas de 10 pacientes fueron \[41.60, 41.48, 42.34, 41.95, 41.86, 42.41, 41.72, 42.26, 41.81, 42.04.\]

Aceptando que la variable aleatoria \(X\)=“grados que dobla la rodilla” sigue una distribución normal, y suponiendo que \(\sigma=0.30\) grados,

1. Obtener un intervalo de confianza para la temperatura media al nivel del 90%.

2. Deduce el tamaño muestral necesario para conseguir un intervalo de confianza al 99%, con un error menor o igual que 0.05.

Solución

1. Sabemos que \(\sigma=0\).\(3\) y \(n=10\)

La media muestral es \(\bar{x}=\dfrac{1}{n}{{\displaystyle\sum_{i=1}^{10}}x_i}=\dfrac{419.47}{10}=41.947\)

El I.C. para \(\mu\) al nivel de confianza \(1-\alpha\) es:

\[ \left(\bar{x}- z_{\alpha /2}\dfrac{\sigma }{\sqrt{n}},\bar{x}+\text{ } z_{\alpha /2}\dfrac{\sigma }{\sqrt{n}}\right)=\left(41.947\pm z_{\alpha /2}\dfrac{0.3}{\sqrt{10}}\right) \]

donde el valor \(z_{\alpha /2}=1.645\) se puede obtener como

qnorm(0.1/2)

## [1] -1.645

es decir, calculamos el cuantil de una normal (por defecto, los parámetros \(0\) y \(1\) no hace falta escribirlos) mediante qnorm.

El I.C. para \(\mu\) al \(95\%\) es, entonces:

\[ (41.947\pm 1.96\cdot \frac{0.3}{\sqrt{10}})=(41.947\pm 0.186 )= (41.761, 42.133). \]

2. Escribimos de nuevo la formula del intervalo de confianza: \[\left(\bar{x}- z_{\alpha /2}\cdot \dfrac{\sigma }{\sqrt{n}},\ \bar{x}+ z_{\alpha /2}\dfrac{\sigma }{\sqrt{n}} \right),\]

para ver que, con una probabilidad \(1-\alpha\) el parámetro verdadero (\(\mu\)) está dentro de ese intervalo; es decir, que la distancia entre \(\mu\) y \(\bar{x}\) es, como mucho, \(z_{\alpha /2}\cdot\dfrac{\sigma }{\sqrt{n}}\).

Esto es, el error de estimación está acotado: \[|\bar{x}-\mu| \leq z_{\alpha /2}\cdot \dfrac{\sigma }{\sqrt{n}} \]

Si queremos calcular el tamaño muestral necesario para que el error sea menor o igual a una cantidad \(e\) (0.05 en este caso), hacemos \[ z_{\alpha /2}\cdot \dfrac{\sigma }{\sqrt{n}}\leq e\iff n\geq \dfrac{ z _{\alpha /2}^{2}\cdot \sigma ^{2}}{e^{2}}= \left(\dfrac{1.96 \cdot 0.3}{0.05}\right)^2=138.298. \]

Hay que tomar entonces \(n=139\) mediciones.

Fijémonos en que, si quisiésemos -con la misma confianza- obtener un error la mitad de pequeño (\(e/2\)), la fórmula que obtenemos es \[ n\geq \frac{ z _{\alpha /2}^{2}\cdot \sigma ^{2}}{(e/2)^{2}}= 4\times \dfrac{ z _{\alpha /2}^{2}\cdot \sigma ^{2}}{e^{2}}, \] es decir, habría que tomar una muestra 4 veces más grande.

Regla de la raiz de n: “si quieres multiplicar la exactitud de una investigación, no basta con duplicar el esfuerzo, debes multiplicarlo por 4”.

‘S. Stigler (Stigler 1986)’

Bibliografía

Stigler, Stephen M. 1986. The History of Statistics: The Measurement of Uncertainty Before 1900. Harvard University Press.