4.2 Non-equally likely outcomes: A weighted die
In the previous section we considered a fair four-sided die.
Now consider the weighted die in Example 2.33: a single roll results in 1 with probability 1/10, 2 with probability 2/10, 3 with probability 3/10, and 4 with probability 4/10.
Let \(\textrm{Q}\) be the probability measure corresponding to the assumption that the die is weighted as in Example 2.33.
We can specify non-equally likely outcomes in BoxModel using the probs option.
The probability space Q in the following code corresponds to a single roll of the weighted die.
Note that \(U\) is still defined via the identity function \(U(\omega) = \omega\). (Recall that a Symbulate RV is always defined in terms of a probability space and a function RV(probspace, function). The default function is the identity: \(g(\omega) = \omega\).)
Q = BoxModel([1, 2, 3, 4], probs = [0.1, 0.2, 0.3, 0.4], size = 1)
U = RV(Q)
U.sim(10000).plot()
plt.show()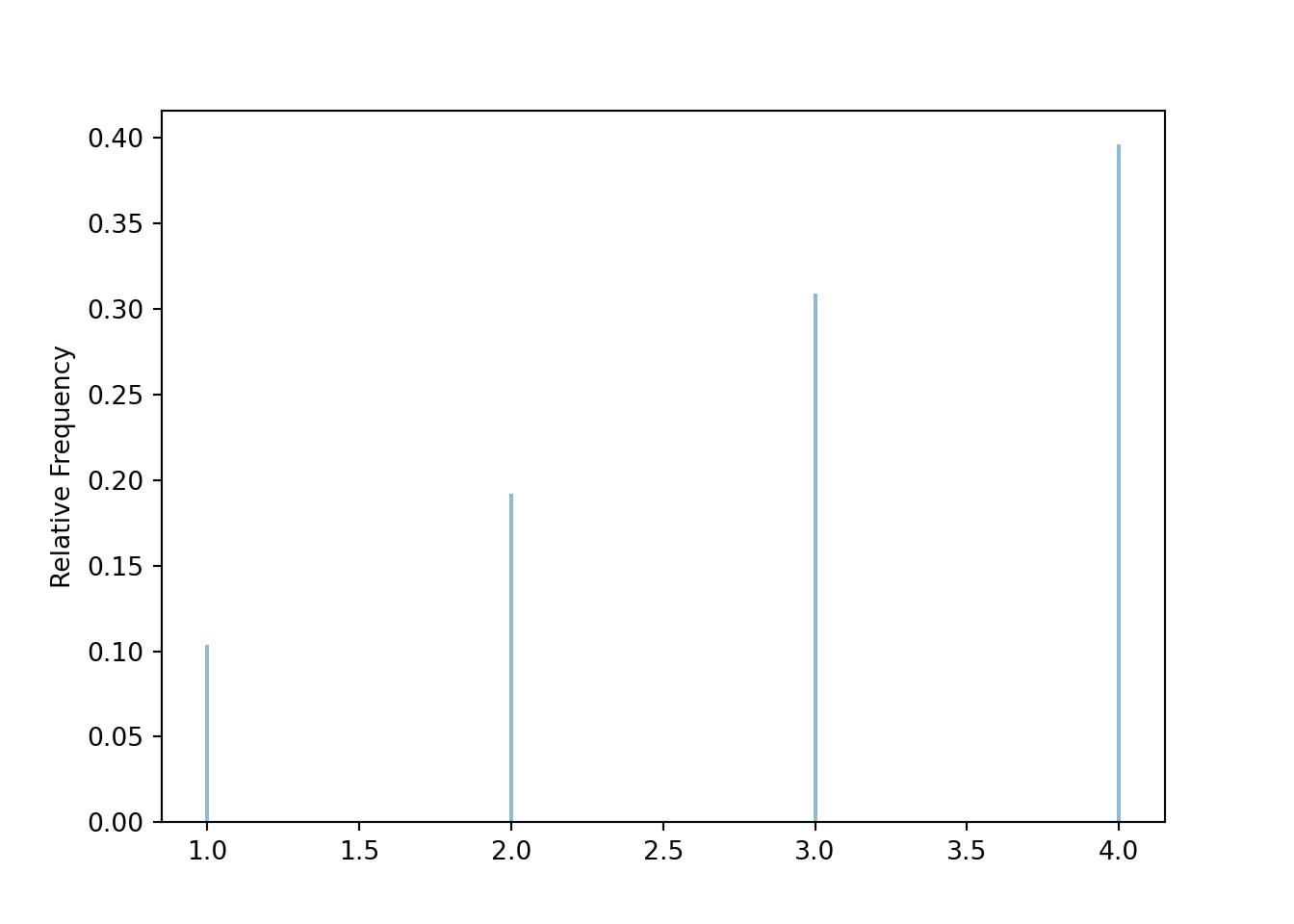
The plot displays a simulation-based approximation to the distribution of \(U\), but now according to the probability measure \(\textrm{Q}\). This distribution can be represented by the middle spinner in Figure 2.9.
In the two scenarios — fair die versus weighted die —
- the sample space is the same, \(\Omega=\{1,2,3,4\}\), and
- the random variable is the same function, \(U(\omega) = \omega\).
What changes is the probability measure, from \(\textrm{P}\) (fair die) to \(\textrm{Q}\) (weighted die). Changing the probability measure changes the distribution of \(U\).
Another way to model a weighted die is with a box model with 10 tickets — one ticket labeled 1, two tickets labeled 2, three tickets labeled 3, and four tickets labeled 4 — from which a single ticket is drawn. A BoxModel can be specified in this way using the following {label: number of tickets with the label} formulation74. This formulation is especially useful when multiple tickets are drawn from the box without replacement.
Q = BoxModel({1: 1, 2: 2, 3: 3, 4: 4}, size = 1)
U = RV(Q)
U.sim(10000).plot()
plt.show()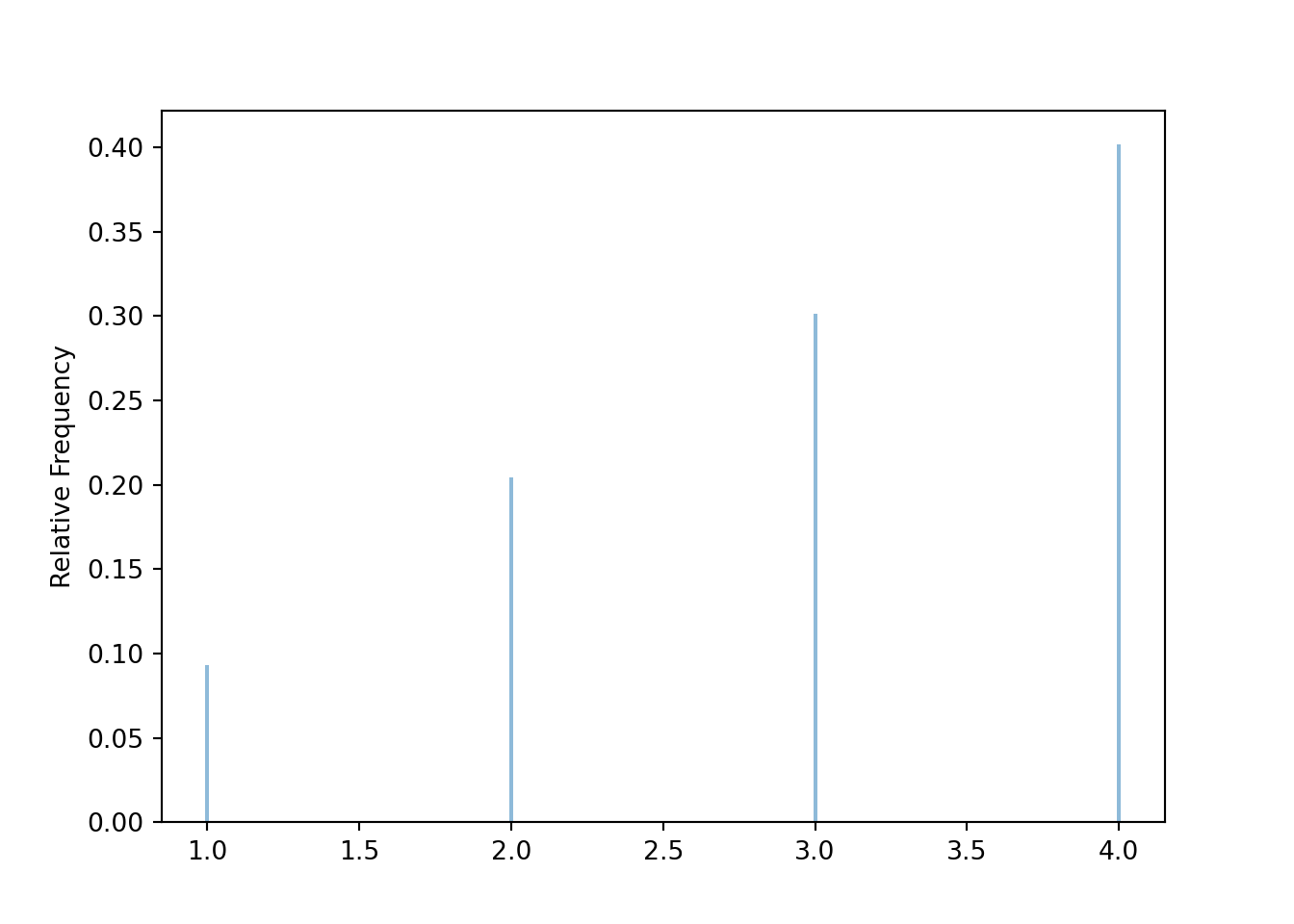
4.2.1 Summary
- Changing a probability measure changes distributions of random variables.
- Distributions can be represented by spinners.
- Box models can handle situations with non-equally likely outcomes.
In Symbulate,
BoxModelhas options likeprobsthat can be used to specify probabilities of individual outcomes.
4.2.2 Exercises
Recall Example 2.34. Write the Symbulate code to model this situation, in two ways.
- Using the
probsoption ofBoxModel. - Using the
{label: number of tickets with the label}form ofBoxModel.
- Using the
Braces
{}are used here because this defines a Python dictionary. But don’t confuse this code with set notation.↩︎