4.6 Distributions of transformations of random variables

It is common in many scientific, mathematical, and statistical context to transform variables. A function of a random variable is a random variable: if $X$ is a random variable and $g$ is a function then $Y=g(X)$ is a random variable. Since $g(X)$ is a random variable it has a distribution. In general, the distribution of $g(X)$ will have a different shape than the distribution of $X$. This section discusses some techniques for determining how a transformation changes the shape of a distribution.

4.6.1 Linear rescaling

In general, the distribution of $g(X)$ will have a different shape than the distribution of $X$. The exception is when $g$ is a linear rescaling.

A linear rescaling is a transformation of the form $g(u) = a +bu$, where $a$ (intercept) and $b$ (slope¹¹⁴) are constants. For example, converting temperature from Celsius to Fahrenheit using $g(u) = 32 + 1.8u$ is a linear rescaling.

A linear rescaling “preserves relative interval length” in the following sense.

If interval A and interval B have the same length in the original measurement units, then the rescaled intervals A and B will have the same length in the rescaled units. For example, [0, 10] and [10, 20] Celsius, both length 10 degrees Celsius, correspond to [32, 50] and [50, 68] Fahrenheit, both length 18 degrees Fahrenheit.
If the ratio of the lengths of interval A and B is $r$ in the original measurement units, then the ratio of the lengths in the rescaled units is also $r$. For example, [10, 30] is twice as long as [0, 10] in Celsius; for the corresponding Fahrenheit intervals, [50, 86] is twice as long as [32, 50].

Think of a linear rescaling as just a consistent relabeling of the variable axis; every 1 unit increment in the original scale corresponds to a $b$ unit increment in the linear rescaling.

Suppose that SAT Math score $X$ follows a Uniform(200, 800) distribution. (It doesn’t but go with in for now). One way to simulate values of $X$ is to simulate values of $U$ from a Uniform(0, 1) distribution and let $X = 200 + (800 - 200)U= 200 + 600U$. Then $X$ is a linear rescaling of $U$, and $X$ takes values in the interval [200, 800]. We can define and simulate values of $X$ in Symbulate. Before looking at the results, sketch a plot of the distribution of $X$ and make an educated guess for its mean and standard deviation.


U = RV(Uniform(0, 1))

X = 200 + 600 * U

(U & X).sim(10)

Index	Result
0	(0.7809949800181978, 668.5969880109187)
1	(0.37701552485485357, 426.20931491291213)
2	(0.02279251886555511, 213.67551131933305)
3	(0.8460127202707671, 707.6076321624603)
4	(0.10274816398024877, 261.6488983881493)
5	(0.7217077069820238, 633.0246241892144)
6	(0.05924299775356345, 235.54579865213807)
7	(0.18425557172206009, 310.55334303323605)
8	(0.7749323478530713, 664.9594087118428)
...	...
9	(0.0016251807690379483, 200.97510846142276)

X.sim(10000).plot()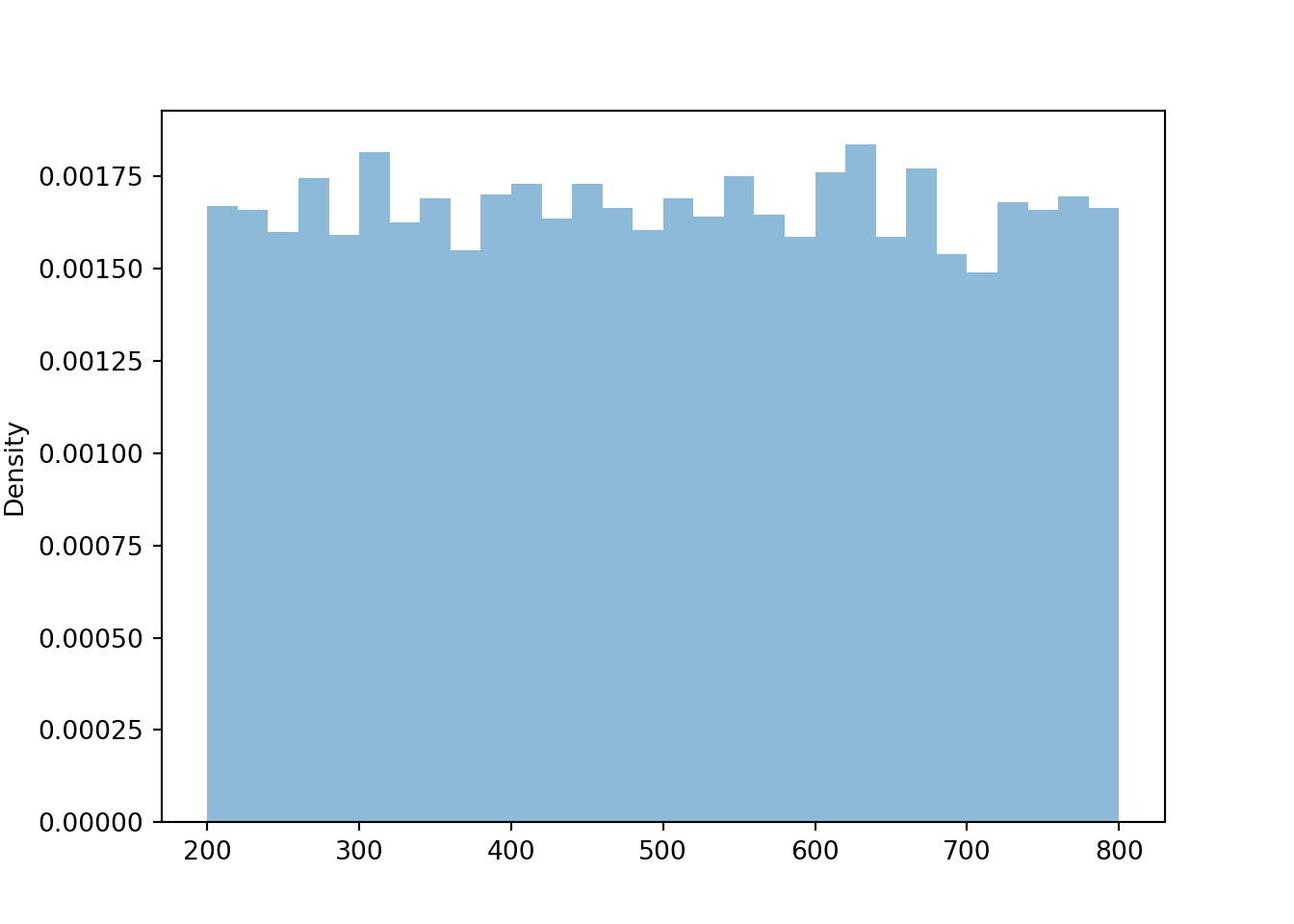

We see that $X$ has a Uniform(200, 800) distribution. The linear rescaling changes the range of possible values, but the general shape of the distribution is still Uniform. We can see why by inspecting a few intervals on both the original and revised scale.

Interval of $U$ values	Probability that $U$ lies in the interval	Interval of $X$ values	Probability that $X$ lies in the interval
(0.0, 0.1)	0.1	(200, 260)	$\frac{60}{600}$
(0.9, 1.0)	0.1	(740, 800)	$\frac{60}{600}$
(0.0, 0.2)	0.2	(200, 320)	$\frac{120}{600}$

For a Uniform distribution the long run average is the midpoint of possible values. The long run average value of $U$ is 0.5, and of $X$ is 500. These two values are related through the same formula mapping $U$ to $X$ values: $500 = 200 + 600\times 0.5$.

U.sim(10000).mean(), X.sim(10000).mean()

## (0.5004958252306164, 498.81665275489985)

For a Uniform distribution, the standard deviation the about 0.289 times the length of the interval: $|b-a|/\sqrt{12}$. The standard deviation of $U$ is about 0.289, and of $X$ is about 173.


U.sim(10000).sd(), X.sim(10000).sd()

## (0.2881066841734862, 172.26255123857297)

The standard deviation of $X$ is 600 times the standard deviation of $U$. Multiplying the $U$ values by 600 rescales the distance between the values. Two values of $U$ that are 0.1 units apart correspond to two values of $X$ that are 60 units apart. A $U$ value of 0.6 is 0.1 units above the mean of $U$, and the corresponding $X$ value 560 is 60 units about the mean of $X$. However, adding the constant 200 to all values just shifts the distribution and does affect degree of variability.

Example 4.24 Let $\textrm{P}$ be the probabilty space corresponding to the Uniform(0, 1) spinner and let $U$ represent the result of a single spin. Define $V=1-U$.

Does $V$ result from a linear rescaling of $U$?
What are the possible values of $V$?
Is $V$ the same random variable as $U$?
Find $\textrm{P}(U \le 0.1)$ and $\textrm{P}(V \le 0.1)$.
Sketch a plot of what the histogram of many simulated values of $V$ would look like.
Does $V$ have the same distribution as $U$?

Solution. to Example 4.24

Show/hide solution

Yes, $V$ result from the linear rescaling $u\mapsto 1-u$ (intercept of 1 and slope of $-1$.)
$V$ takes values in the interval [0,1]. Basically, this transformation just changes the direction of the spinner from clockwise to counterclockwise. The axis on the usual spinner has values $u$ increasing clockwise from 0 to 1. Applying the transformation $1-u$, the values would decrease clockwise from 1 to 0.
No. $V$ and $U$ are different random variables. If the spin lands on $\omega=0.1$, then $U(\omega)=0.1$ but $V(\omega)=0.9$. $V$ and $U$ return different values for the same outcome; they are measuring different things.
$\textrm{P}(U \le 0.1) = 0.1$ and $\textrm{P}(V \le 0.1)=\textrm{P}(1-U \le 0.1) = \textrm{P}(U\ge 0.9) = 0.1$. Note, however, that these are different events: $\{U \le 0.1\}=\{0 \le \omega \le 0.1\}$ while $\{V \le 0.1\}=\{0.9 \le \omega \le 1\}$. But each is an interval of length 0.1 so they have the same probability according to the uniform probability measure.
Since $V$ is a linear rescaling of $U$, the shape of the histogram of simulated values of $V$ should be the same as that for $U$. Also, the possible values of $V$ are the same as those for $U$. So the histograms should look identical (aside from natural simulation variability).
Yes, $V$ has the same distribution as $U$. While for any single outcome (spin), the values of $V$ and $U$ will be different, over many repetitions (spins) the pattern of variation of the $V$ values, as depicted in a histogram, will be identical to that of $U$.


P = Uniform(0, 1)
U = RV(P)

V = 1 - U

V.sim(10000).plot()
plt.show()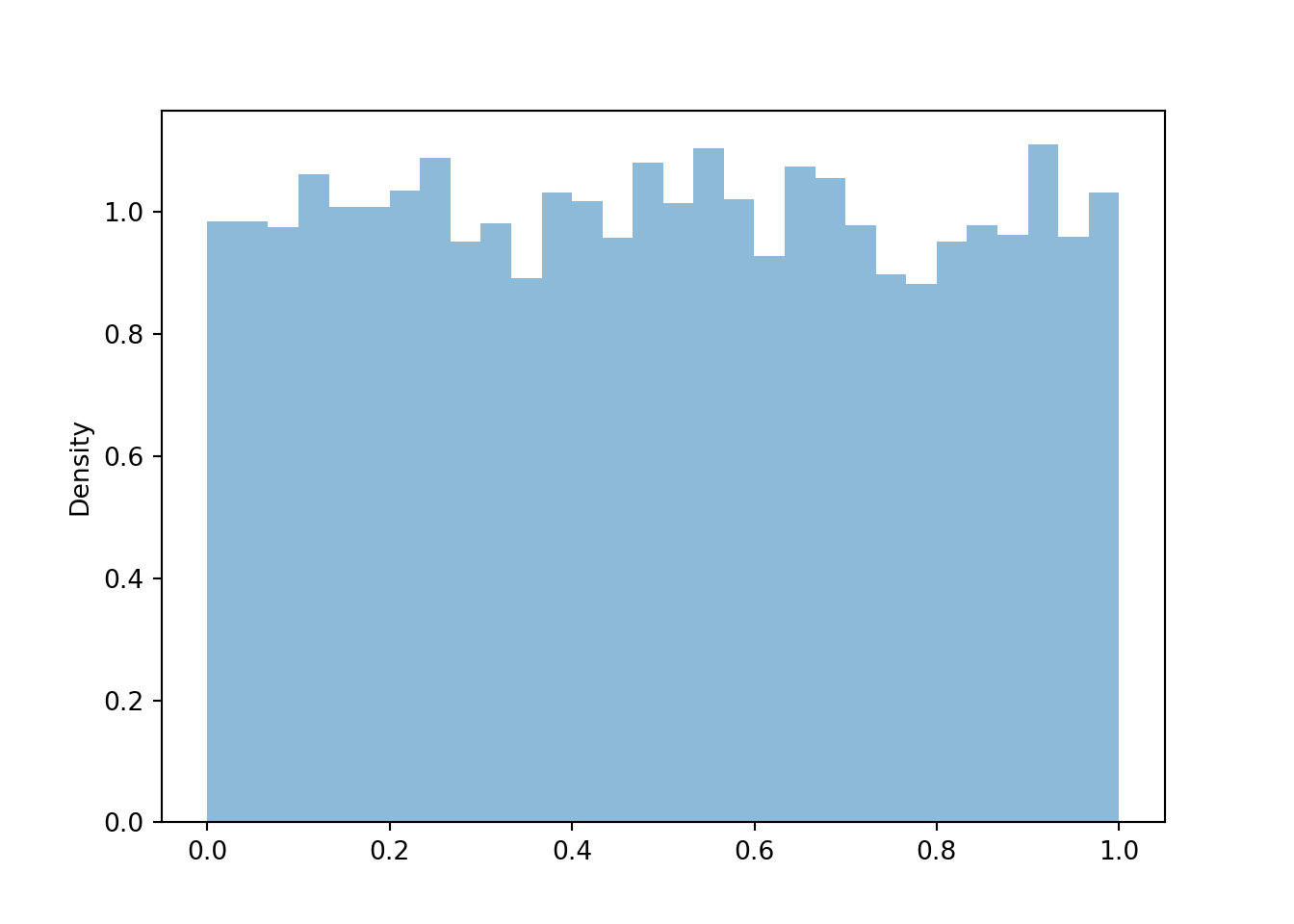

Let’s consider a non-uniform example. Now let’s suppose that SAT Math score $X$ follows a Normal(500, 100) distribution. We can simulate values of $X$ by simulating $Z$ from the standard Normal(0, 1) distribution and setting $X = 500 + 100Z$. (Remember that the standard Normal spinner returns standardized values, so $Z = 1$ corresponds to 1 standard deviation above the mean, that is, $X= 600$.) The reason this works is because the linear rescaling doesn’t change the Normal shape.

Z = RV(Normal(0, 1))

X = 500 + 100 * Z

(Z & X).sim(10)

Index	Result
0	(0.857171958819711, 585.7171958819711)
1	(-0.23982160072061062, 476.01783992793895)
2	(1.252689055020093, 625.2689055020093)
3	(-0.4964317510937479, 450.3568248906252)
4	(0.9269673547550576, 592.6967354755058)
5	(0.4828829989503202, 548.288299895032)
6	(-0.8363052525418587, 416.36947474581416)
7	(-1.179120842853697, 382.0879157146303)
8	(-0.1082183137094412, 489.1781686290559)
...	...
9	(-0.36405518219878696, 463.5944817801213)

x = X.sim(10000)

x.plot() # plot the simulated values
Normal(500, 100).plot() # plot the theoretical density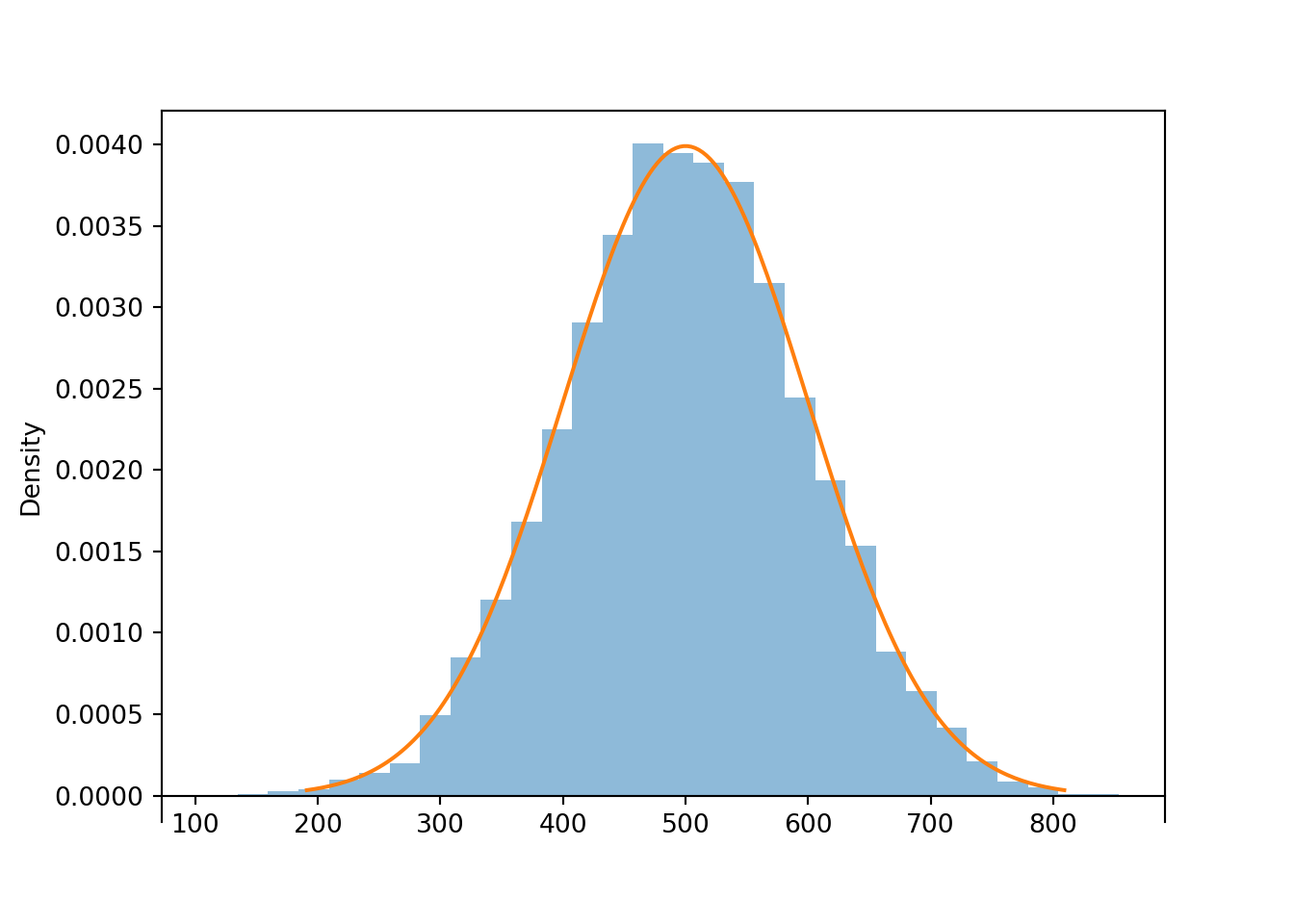

x.mean(), x.sd()

## (499.71181362823285, 98.84002683251305)

The linear rescaling changes the range of observed values; almost all of the values of $Z$ lie in the interval $(-3, 3)$ while almost all of the values of $X$ lie in the interval $(200, 800)$. However, the distribution of $X$ still has the general Normal shape. The means are related by the conversion formula: $500 = 500 + 100 \times 0$. Multiplying the values of $Z$ by 100 rescales the distance between values; two values of $Z$ that are 1 unit apart correspond to two values of $X$ that are 100 units apart. However, adding the constant 500 to all the values just shifts the center of the distribution and does not affect variability. Therefore, the standard deviation of $X$ is 100 times the standard deviation of $Z$.

In general, if $Z$ has a Normal(0, 1) distribution then $X = \mu + \sigma Z$ has a Normal($\mu$, $\sigma$) distribution.

Example 4.25 Suppose that $X$, the SAT Math score of a randomly selected student, follows a Normal(500, 100) distribution. Randomly select a student and let $X$ be the student’s SAT Math score. Now have the selected student spin the Normal(0, 1) spinner. Let $Z$ be the result of the spin and let $Y=500 + 100 Z$.

Is $Y$ the same random variable as $X$?
Does $Y$ have the same distribution as $X$?

Solution. to Example 4.25

Show/hide solution

No, these two random variables are measuring different things. One is measuring SAT Math score; one is measuring what comes out of a spinner. Taking the SAT and spinning a spinner are not the same thing.
Yes, they do have the same distribution. Repeating the process of randomly selecting a student and measuring SAT Math score will yield values that follow a Normal(500, 100) distribution. Repeating the process of spinning the Normal(0, 1) spinner to get $Z$ and then setting $Y=500+100Z$ will also yield values that follow a Normal(500, 100) distribution. Even though $X$ and $Y$ are different random variables they follow the same long run pattern of variability.

Example 4.26 Let $Z$ be a random variable with a Normal(0, 1) distribution. Consider $-Z$.

Donny Don’t says that the distribution of $-Z$ will look like an “upside-down bell”. Is Donny correct? If not, explain why not and describe the distribution of $-Z$.
Donny Don’t says that the standard deviation of $-Z$ is -1. Is Donny correct? If not, explain why not and determine the standard deviation of $-Z$.

Solution. to Example 4.26

Show/hide solution

Donny is confusing a random variable with its distribution. The values of the random variable are multiplied by -1, not the heights of the histogram. Multiplying values of $Z$ by -1 rotates the “bell” about 0 horizontally (not vertically). Since the Normal(0, 1) distribution is symmetric about 0, the distribution of $-Z$ is the same as the distribution of $Z$, Normal(0, 1).
Standard deviation cannot be negative. Standard deviation measures average distance of values from the mean. A $Z$ value of 1 yields a $-Z$ value of -1; in either case the value is 1 unit away from the mean. Multiplying a random variable by $-1$ simply reflects the values horizontally about 0, but does not change distance from the mean¹¹⁵. In general, $X$ and $-X$ have the same standard deviation. In this example we can say more: $Z$ and $-Z$ have the same distribution so they must have the same standard deviation, 1.

4.6.1.1 Summary

A linear rescaling is a transformation of the form $g(u) = a + bu$.
A linear rescaling of a random variable does not change the basic shape of its distribution, just the range of possible values.
- However, remember that the possible values are part of the distribution. So a linear rescaling does technically change the distribution, even if the basic shape is the same. (For example, Normal(500, 100) and Normal(0, 1) are two different distributions.)
A linear rescaling transforms the mean in the same way the individual values are transformed.
Adding a constant to a random variable does not affect its standard deviation.
Multiplying a random variable by a constant multiplies its standard deviation by the absolute value of the constant.
Whether in the short run or the long run, \[\begin{align*} \text{Average of $a+bX$} & = a+b(\text{Average of $X$})\\ \text{SD of $a+bX$} & = |b|(\text{SD of $X$})\\ \text{Variance of $a+bX$} & = b^2(\text{Variance of $X$}) \end{align*}\]
If $U$ has a Uniform(0, 1) distribution then $X = a + (b-a)U$ has a Uniform($a$, $b$) distribution.
If $Z$ has a Normal(0, 1) distribution then $X = \mu + \sigma Z$ has a Normal($\mu$, $\sigma$) distribution.
Remember, do NOT confuse a random variable with its distribution.
- The random variable is the numerical quantity being measured
- The distribution is the long run pattern of variation of many observed values of the random variable

4.6.2 Nonlinear transformations of random variables

A linear rescaling does not change the shape of a distribution, only the range of possible values. But what about a nonlinear transformation, like a logarithmic or square root transformation? In contrast to a linear rescaling, a nonlinear rescaling does not preserve relative interval length, so we might expect that a nonlinear rescaling can change the shape of a distribution. We’ll investigate by considering the Uniform(0, 1) spinner and a logarithmic¹¹⁶ transformation.

Let $U$ represent the result of a single spin of the Uniform(0, 1) spinner. We’ll basically consider $\log(U)$, but this leads to to two minor technicalities.

Since $U\in[0, 1]$, $\log(U)\le 0$. To obtain positive values we consider $-\log(U)$, which takes values in $[0,\infty)$.
Technically, applying $-\log(u)$ to the values on the axis of the Uniform(0, 1) spinner, the resulting values would decrease from $\infty$ to 0 clockwise. To make the values start at 0 and increase to $\infty$ clockwise, we consider $-\log(1-U)$. (We saw in the previous section the transformation $u \to 1-u$ basically just changes direction from clockwise to counterclockwise.)

Therefore, it’s a little more convenient to consider the random variable $X=-\log(1-U)$ which takes values in $[0,\infty)$. It also turns out, as we saw in earlier, that $-\log(1-u)$ is the quantile function of the Exponential(1) distribution. We have already seen that $X$ has an Exponential(1) distribution. Now we’ll take a closer look why.

The following code defines $X$ and plots a few simulated values.

P = Uniform(0, 1)
U = RV(P)

X = -log(1 - U)

x = X.sim(100)

x.plot('rug')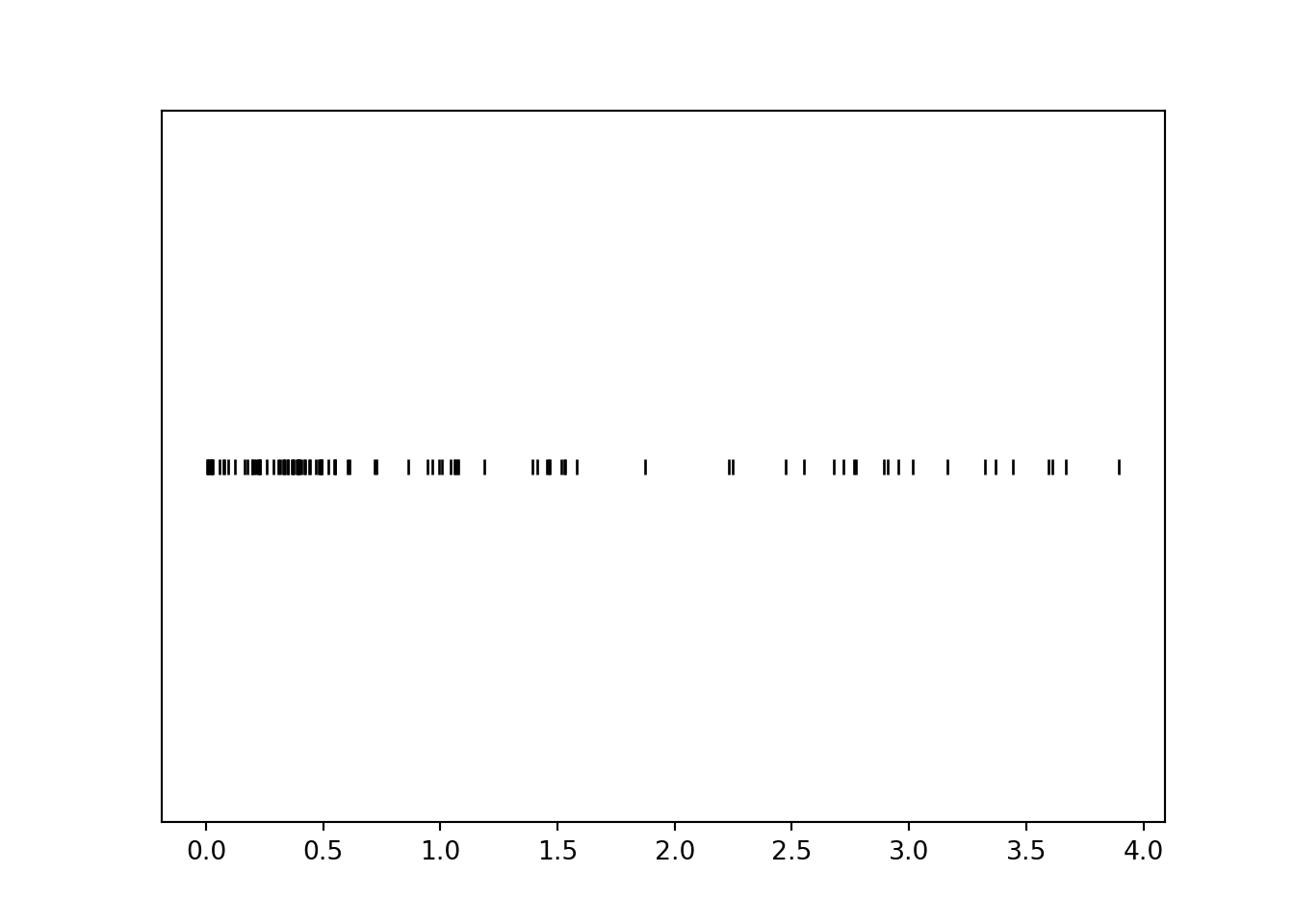

Notice that values near 0 occur with higher frequency than larger values. For example, there are many more simulated values of $X$ that lie in the interval $[0, 1]$ than in the interval $[3, 4]$, even though these intervals both have length 1. Let’s see why this is happening.

Example 4.27 For each of the intervals in the table below find the probability that $U$ lies in the interval, and identify the corresponding values of $X$. (You should at least compute a few by hand to see what’s happening, but you can use software to fill in the rest.) After completing the table, sketch a histogram representing the distribution of $X$.

Interval of U	Length of U interval	Probability	Interval of X	Length of X interval
(0, 0.1)
(0.1, 0.2)
(0.2, 0.3)
(0.3, 0.4)
(0.4, 0.5)
(0.5, 0.6)
(0.6, 0.7)
(0.7, 0.8)
(0.8, 0.9)
(0.9, 1)

Solution. to Example 4.27

Plug the endpoints into the conversion formula $u\mapsto -\log(1-u)$ to find the corresponding $X$ interval. For example, the $U$ interval $(0.1, 0.2)$ corresponds to the $X$ interval $(-\log(1-0.1), -\log(1-0.2)) = (0.105, 0.223)$. Since $U$ has a Uniform(0, 1) distribution the probability is just the length of the $U$ interval.

Interval of U	Length of U interval	Probability	Interval of X	Length of X interval
(0, 0.1)	0.1	0.1	(0, 0.105)	0.105
(0.1, 0.2)	0.1	0.1	(0.105, 0.223)	0.118
(0.2, 0.3)	0.1	0.1	(0.223, 0.357)	0.134
(0.3, 0.4)	0.1	0.1	(0.357, 0.511)	0.154
(0.4, 0.5)	0.1	0.1	(0.511, 0.693)	0.182
(0.5, 0.6)	0.1	0.1	(0.693, 0.916)	0.223
(0.6, 0.7)	0.1	0.1	(0.916, 1.204)	0.288
(0.7, 0.8)	0.1	0.1	(1.204, 1.609)	0.405
(0.8, 0.9)	0.1	0.1	(1.609, 2.303)	0.693
(0.9, 1)	0.1	0.1	(2.303, Inf)	Inf

We see that the logarithmic transformation does not preserve relative interval length. Each of the original intervals of $U$ values has the same length, but the nonlinear logarithmic transformation “stretches out” these intervals in different ways. The probability that $U$ lies in each of these intervals is 0.1. As the transformation stretches the intervals, the 0.1 probability gets “spread” over intervals of different length. Since probability/relative frequency is represented by area in a histogram, if two regions of differing length have the same area, then they must have different heights. Thus the shape of the distribution of $X$ will not be Uniform.

The following plot illustrates the results of Example 4.27. Each bar in the top histogram corresponds to the same color bar in the bottom histogram. All bars have area 0.1. In the top histogram, the bins have equal width so the heights are the same. However, in the bottom histogram the bars have different widths but the same area, so they must have different heights, and we start to see where the Exponential(1) shape comes from.

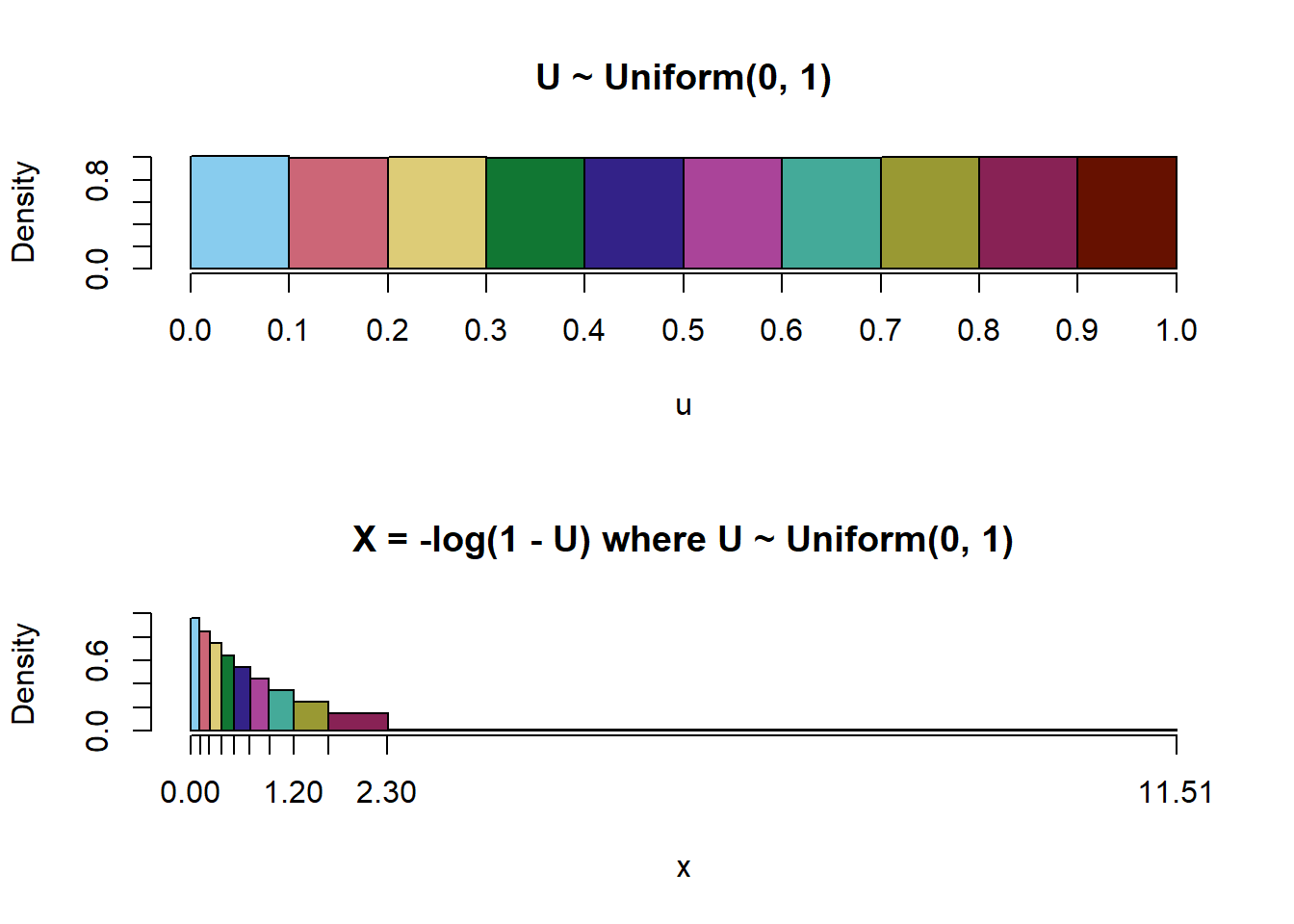
The following example provides a similar illustration, but from the reverse perspective.

Example 4.28 For each of the intervals of $X$ values in the table below identify the corresponding values of $U$, and then find the probability that $X$ lies in the interval. (You should at least compute a few by hand to see what’s happening, but you can use software to fill in the rest.) After completing the table, sketch a histogram representing the distribution of $X$. Hint: if $X = -\log(1-U)$ then $U = 1-e^{-X}$.

Interval of X	Length of X interval	Probability	Interval of U	Length of U interval
(0, 0.5)
(0.5, 1)
(1, 1.5)
(1.5, 2)
(2, 2.5)
(2.5, 3)
(3, 3.5)
(3.5, 4)
(4, 4.5)
(4.5, 5)

Solution. to Example 4.28

The corresponding $U$ intervals are obtained by applying the inverse transformation $v\mapsto 1-e^{-v}$. For example, the $X$ interval $(0.5, 1)$ corresponds to the $U$ interval $(1-e^{-0.5}, 1-e^{-1}) = (0.393, 0.632)$.

Interval of X	Length of X interval	Probability	Interval of U	Length of U interval
(0, 0.5)	0.5	0.393	(0, 0.393)	0.393
(0.5, 1)	0.5	0.239	(0.393, 0.632)	0.239
(1, 1.5)	0.5	0.145	(0.632, 0.777)	0.145
(1.5, 2)	0.5	0.088	(0.777, 0.865)	0.088
(2, 2.5)	0.5	0.053	(0.865, 0.918)	0.053
(2.5, 3)	0.5	0.032	(0.918, 0.95)	0.032
(3, 3.5)	0.5	0.020	(0.95, 0.97)	0.020
(3.5, 4)	0.5	0.012	(0.97, 0.982)	0.012
(4, 4.5)	0.5	0.007	(0.982, 0.989)	0.007
(4.5, 5)	0.5	0.004	(0.989, 0.993)	0.004

Since $U$ has a Uniform(0, 1) distribution the probability is just the length of the $U$ interval. Each of the $X$ intervals has the same length but they correspond to intervals of differing length in the original $U$ scale, and hence intervals of different probability.

The following plot illustrates the results of Example 4.28 (plots on the right). These two examples give some insight into how the transformed random variable $X = -\log(1-U)$ has an Exponential(1) distribution.

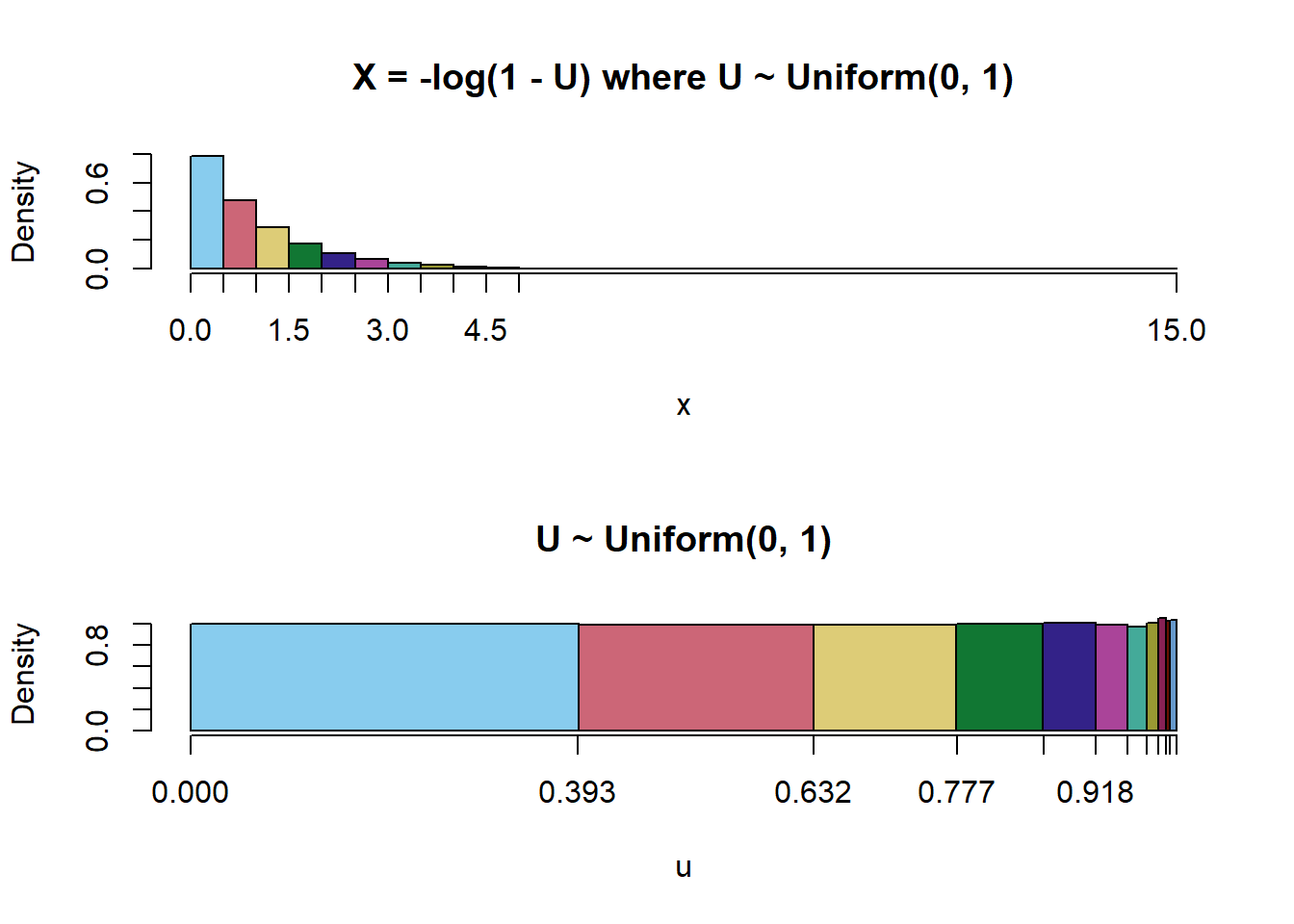
“Spreadsheet” calculations like those in the previous two examples can help when sketching the distribution of a transformed random variable.

For a linear rescaling, we could just plug the mean of the original variable into the conversion formula to find the mean of the transformed variable. However, this will not work for nonlinear transformations.


(U & X).sim(10000).mean()

## (0.5005896607918349, 0.997577838817509)

We know that since $U$ has a Uniform(0, 1) distribution its long run average value is 0.5, and since $X$ has an Exponential(1) distribution its long run average value is 1, but $-\log(1 - 0.5) \neq 1$. The nonlinear “stretching” of the axis makes some value relatively larger and others relatively smaller than they were on the original scale, which influences the average. Remember, in general: whether in the short run or the long run \[ \text{Average of } g(X) \neq g(\text{Average of }X). \]

Recall that a function of a random variable is also a random variable. If $X$ is a random variable, then $Y=g(X)$ is also a random variable and so it has a probability distribution. Unless $g$ represents a linear rescaling, a transformation will change the shape of the distribution. So the question is: what is the distribution of $g(X)$? We’ll focus on transformations of continuous random variables, in which case the key to answering the question is to work with cdfs.

Example 4.29 We have now seen a few reasons why if $U$ has a Uniform(0, 1) distribution then $X=-\log(1-U)$ has an Exponential(1) distribution. The purpose of the example is derive the pdf of $X$, starting from just the setup in the previous sentence.

Identify the possible values of $X$. (We have done this already, but this should always be your first step.)
Let $F_X$ denote the cdf of $X$. Find $F_X(1)$.
Find $F_X(2)$.
Find the cdf $F_X(x)$.
Find the pdf $f_X(x)$.
Why should we not be surprised that $X=-\log(1-U)$ has cdf $F_X(x) = 1 - e^{-x}$? Hint: what is the function $u\mapsto -\log(1-u)$ in this case?

Solution. to Example 4.29

Show/hide solution

As always, first determine the range of possible values. When $u=0$, $-\log(1-u)=0$, and as $u$ approaches 1, $-\log(1-u)$ approaches $\infty$; see the picture of the function below. So $X$ takes values in $[0, \infty)$.
$F_X(1) = \textrm{P}(X \le 1)$, a probability statement involving $X$. Since we know the distribution of $U$, we express the event $\{X \le 1\}$ as an equivalent event involving $U$.
\[ \{X \le 1\} = \{-\log(1-U) \le 1\} = \{U \le 1 - e^{-1}\} \] The above follows since $-\log(1-u)\le 1$ if and only if $u\le 1-e^{-1}$; see Figure 4.22 below. Therefore \[ F_X(1) = \textrm{P}(X \le 1) = \textrm{P}(-\log(1-U)\le 1) = \textrm{P}(U\le 1-e^{-1}) \] Now since $U$ has a Uniform(0, 1) distribution, $\textrm{P}(U\le u)=u$ for $0<u<1$. The value $1-e^{-1}\approx 0.632$ is just a number between 0 and 1, so $\textrm{P}(U\le 1-e^{-1}) = 1-e^{-1}\approx 0.632$. Therefore $F_X(1)=1-e^{-1}\approx 0.632$.
Similar to the previous part \[ F_X(2) = \textrm{P}(X \le 2) = \textrm{P}(-\log(1-U)\le 2) = \textrm{P}(U\le 1-e^{-2}) = 1-e^{-2}\approx 0.865 \]
As suggested in the paragraph before the example, the key to finding the pdf is to work with cdfs. We basically repeat the calculation in the previous steps, but for a generic $x$ instead of 1 or 2. Consider $0\le x<\infty$; we wish to find the cdf evaluated at $x$. \[ F_X(x) = \textrm{P}(X \le x) = \textrm{P}(-\log(1-U)\le x) = \textrm{P}(U \le 1-e^{-x}) = 1-e^{-x} \] The above follows since, for $0<x<\infty$, $-\log(1-u)\le x$ if and only if $u\le 1-e^{-x}$; see Figure 4.22 below (illustrated for $x=1$). Now since $U$ has a Uniform(0, 1) distribution, $\textrm{P}(U\le u)=u$ for $0<u<1$. For a fixed $0<x<\infty$, the value $1-e^{-x}$ is just a number between 0 and 1, so $\textrm{P}(U\le 1-e^{-x}) = 1-e^{-x}$. Therefore $F_X(x)=1-e^{-x}, 0<x<\infty$.
From the previous part, we see that the cdf of $X$ is the cdf of the Exponential(1) distribution, so that is enough to show that $X$ has a Exponential(1) distribution. But we can also directly differentiate the cdf with respective to $x$ to find the pdf. \[ f_X(x) = F'(x) =\frac{d}{dx}(1-e^{-x}) = e^{-x}, \qquad 0<x<\infty \] Thus we see that $X$ has the Exponential(1) pdf.
The function $Q_X(u) = -\log(1-u)$ is the quantile function (inverse cdf) corresponding to the cdf $F_X(x) = 1-e^{-x}$. Therefore, since $U$ has a Uniform(0, 1) distribution, the random variable $Q_X(U)$ will have cdf $F_X$ by universality of the Uniform.

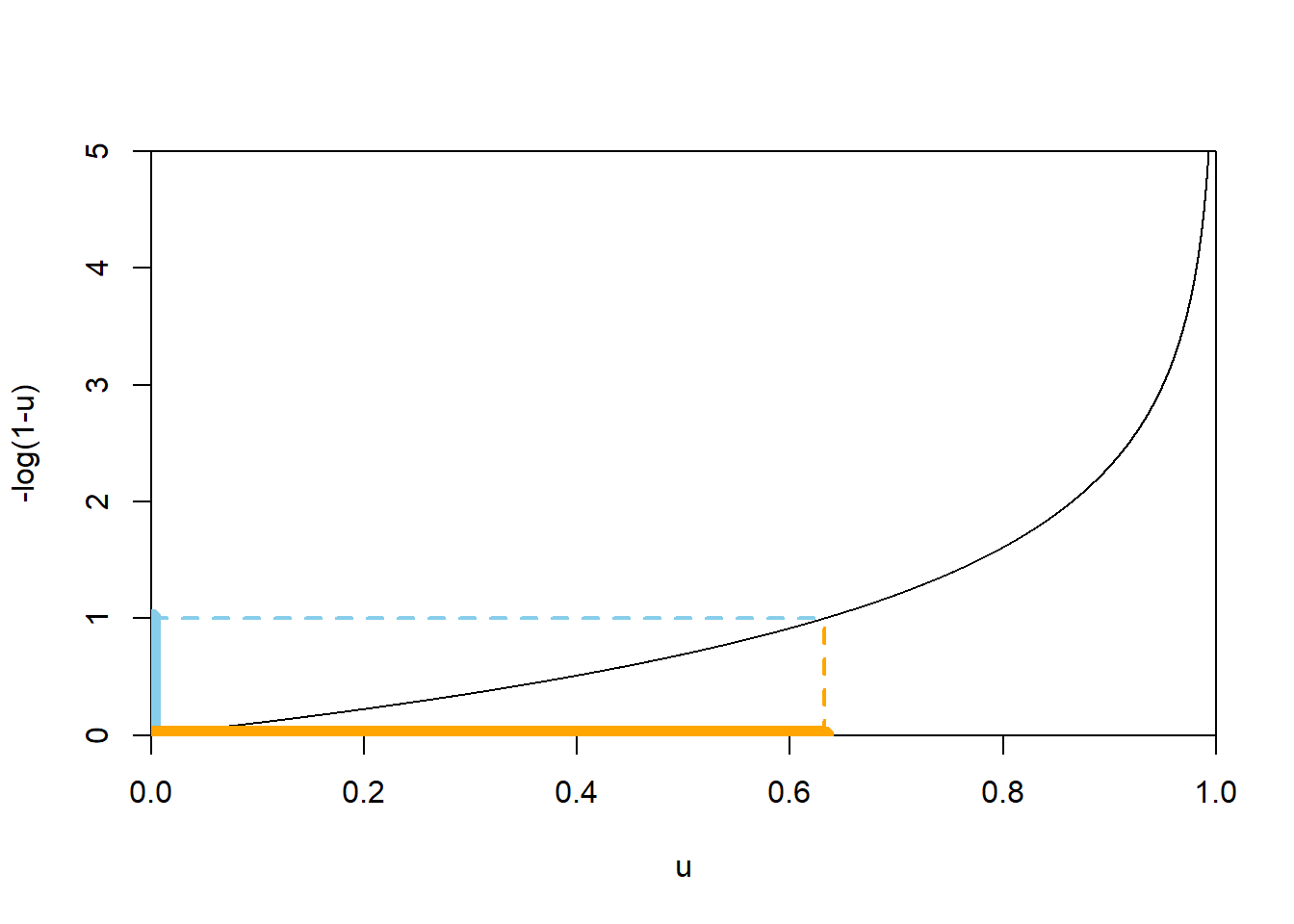
$A plot of the function $u\mapsto -\log(1-u)$. The dotted lines illustrate that $-\log(1-u)\le 1$ if and only if $u\le 1-e^{-1}\approx 0.632$.$

Figure 4.22: A plot of the function $u\mapsto -\log(1-u)$. The dotted lines illustrate that $-\log(1-u)\le 1$ if and only if $u\le 1-e^{-1}\approx 0.632$.

If $X$ is a continuous random variable whose distribution is known, the cdf method can be used to find the pdf of $Y=g(X)$

Determine the possible values of $Y$. Let $y$ represent a generic possible value of $Y$.
The cdf of $Y$ is $F_Y(y) = \textrm{P}(Y\le y) = \textrm{P}(g(X) \le y)$.
Rearrange $\{g(X) \le y\}$ to get an event involving $X$. Warning: it is not always $\{X \le g^{-1}(y)\}$. Sketching a picture of the function $g$ helps.
Obtain an expression for the cdf of $Y$ which involves $F_X$ and some transformation of the value $y$.
Differentiate the expression for $F_Y(y)$ with respect to $y$, and use what is known about $F'_X = f_X$, to obtain the pdf of $Y$. You will typically need to apply the chain rule when differentiating.

You will need to use information about $X$ at some point in the last step above. You can either:

Plug in the cdf of $X$ and then differentiate with respect to $y$.
Differentiate with respect to $y$ and then plug in the pdf of $X$.

Either way gets you to the correct answer, but depending on the problem one way might be easier than the other. We’ll illustrate both methods in the next example.

Example 4.30 Let $X$ be a random variable with a Uniform(-1, 1) distribution and Let $Y=X^2$.

Identify the possible values of $Y$.
Sketch the pdf of $Y$. Hint: consider a few equally spaced intervals of $Y$ values and see what $X$ values they correspond to.
Run a simulation to approximate the pdf of $Y$.
Find $F_Y(0.49)$.
Use the cdf method to find the pdf of $Y$. Is the pdf consistent with your simulation results?

Solution. to Example 4.30

Show/hide solution

Always start with the possible values: since $-1< X<1$ we have $0<Y<1$.
The idea to the sketch is that squaring a number less than 1 in absolute value returns a smaller number, e.g. $0.1^2 = 0.01$. So the transformation “pushes values towards 0” making the density higher near 0. Consider the intervals $[0, 0.1]$ and $[0.9, 1]$ on the original scale; both intervals have probability 0.05 under the Uniform($-1, 1$) distribution. On the squared scale, these intervals correspond to $[0, 0.01]$ and $[0.81, 1]$ respectively. So the 0.05 probability is “squished” into $[0, 0.01]$, resulting in a greater height, while it is “spread out” over $[0.81, 1]$ resulting in a smaller height. Remember: probability is represented by area. This gives you an idea that the pdf should be highest at 0 and lowest at 1. To get a better sketch, you can do a “spreadsheet” type calculation; see below. We start with equally spaced intervals on the $Y$ scale and then find the corresponding intervals of $X = \pm\sqrt{Y}$. Since $X$ has a Uniform distribution over an interval of length 2, the probability that $X$ lies in a subinterval of $(-1, 1)$ is the length of the subinterval divided by 2. The evenly spaced $Y$ intervals correspond to differentially spaced $X$ intervals, hence different probabilities/areas, and so the density height of the $Y$ intervals changes accordingly.
See the simulation results below. We see that the density is highest near 0 and lowest near 1.
Since $X$ can take negative values, we have to be careful; see Figure 4.23 below. \[ \{Y \le 0.49\} = \{X^2 \le 0.49\} = \{-\sqrt{0.49} \le X \le \sqrt{0.49}\} \] Therefore, since $X$ has a Uniform($-1,1$) distribution, \[ F_Y(0.49) = \textrm{P}(Y \le 0.49) = \textrm{P}(-0.7 \le X \le 0.7) = \frac{1.4}{2} = 0.7 \]
Fix $0<y<1$. We now do the same calculation in the previous part in terms of a generic $y$, but it often helps to think of $y$ as a particular number first. \[\begin{align*} F_Y(y) & = \textrm{P}(Y\le y)\\ & = \textrm{P}(X^2\le y)\\ & = \textrm{P}(-\sqrt{y}\le X\le \sqrt{y})\\ & = F_X(\sqrt{y}) - F_X(-\sqrt{y}) \end{align*}\] Note that the event of interest is not just $\{X\le \sqrt{y}\}$; see Figure 4.23 below. From here we can either

use the cdf of $X$ and then differentiate, or differentiate and then use the pdf of $X$. We’ll illustrate both.
1. Using the Uniform(-1, 1) cdf, the interval $[-\sqrt{y}, \sqrt{y}]$ has length $2\sqrt{y}$, and the total length of $[-1, 1]$ is 2, so we have \[ F_Y(y) = F_X(\sqrt{y}) - F_X(-\sqrt{y}) = \frac{2\sqrt{y}}{2} = \sqrt{y} \] Now differentiate with respect to the argument $y$ to obtain $f_Y(y) = \frac{1}{2\sqrt{y}}, 0<y<1$.
2. Differentiate both sides of $F_Y(y) = F_X(\sqrt{y}) - F_X(-\sqrt{y})$, with respect to $y$. Differentiating the cdf $F_Y$ yields its pdf $f_Y$, and differentiating the cdf $F_X$ yields its pdf $f_X$. But don’t forget to use the chain rule when differentiating $F_X(\sqrt{y})$. \[\begin{align*} F_Y(y) & = F_X(\sqrt{y}) - F_X(-\sqrt{y})\\ \Rightarrow \frac{d}{dy} F_Y(y) & = \frac{d}{dy}\left(F_X(\sqrt{y}) - F_X(-\sqrt{y})\right)\\ \qquad f_Y(y) & = f_X(\sqrt{y})\frac{1}{2\sqrt{y}} - f_X(-\sqrt{y})\left(-\frac{1}{2\sqrt{y}}\right)\\ &= \frac{1}{2\sqrt{y}}\left(f_X(\sqrt{y})+f_X(-\sqrt{y})\right) \end{align*}\] Since $X$ has a Uniform(-1, 1) distribution, its pdf is $f_X(x) = 1/2, -1<x<1$. But for $0<y<1$, $\sqrt{y}$ and $-\sqrt{y}$ are just numbers in $[-1, 1]$, so $f_X(\sqrt{y})=1/2$ and $f_X(-\sqrt{y})=1/2$. Therefore, $f_Y(y) = \frac{1}{2\sqrt{y}}, 0<y<1$. The histogram of simulated values seems consistent with this shape. (The density blows up at 0.)

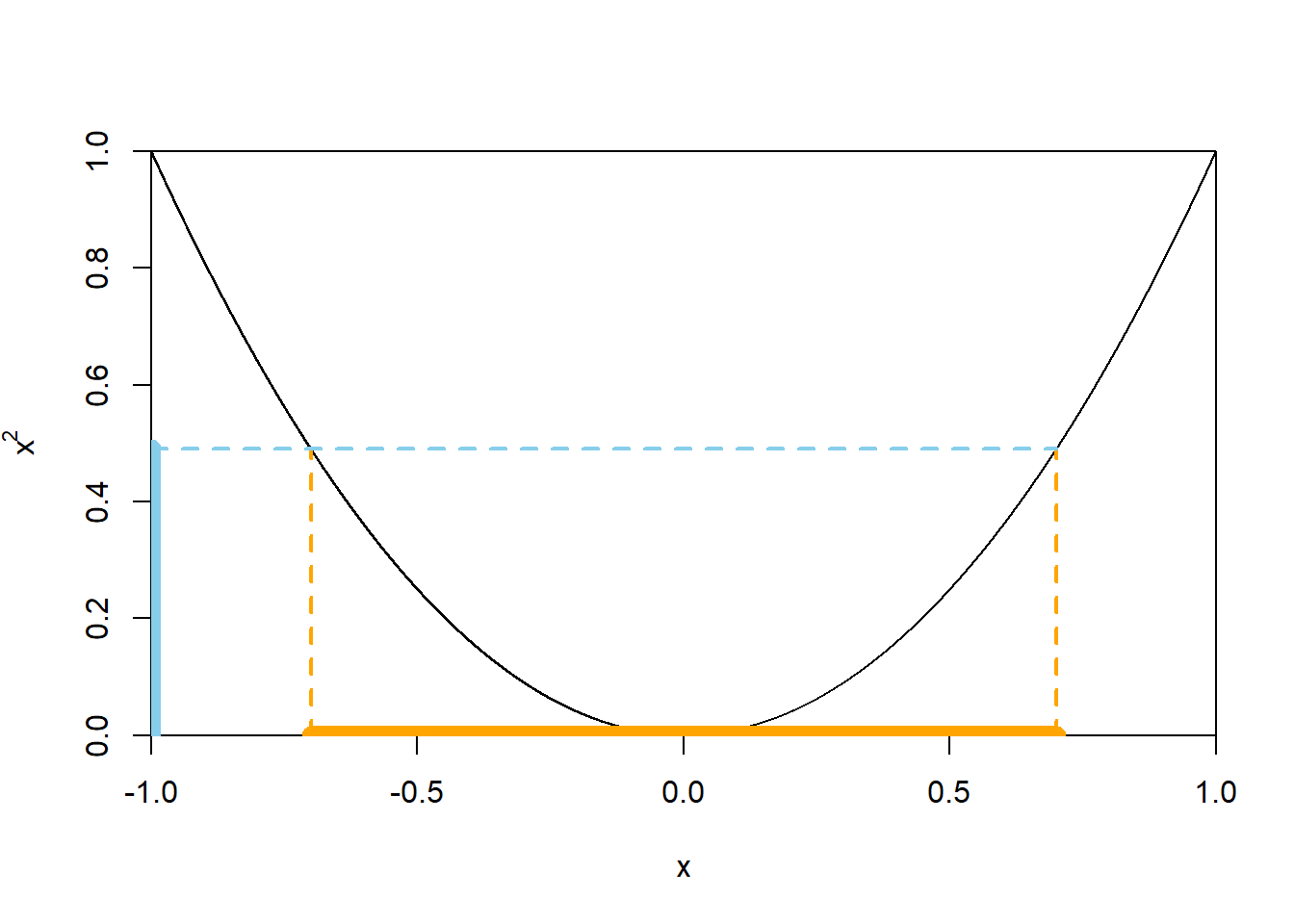
$A plot of the function $x\mapsto x^2$ for $-1<x<1$. The dotted lines illustrate that $x^2\le 0.49$ if and only if $-\sqrt{0.49}\le x\le \sqrt{0.49}$.$

Figure 4.23: A plot of the function $x\mapsto x^2$ for $-1<x<1$. The dotted lines illustrate that $x^2\le 0.49$ if and only if $-\sqrt{0.49}\le x\le \sqrt{0.49}$.

The table below helps us see how the transformation $Y = X^2$ “pushes” density towards 0 if $X$ has a Uniform(-1, 1) distribution.

Y interval	X interval	Length of X interval	Probability	Length of Y interval	Height of Y interval
(0, 0.1)	(-0.3162, 0) U (0,0.3162)	0.6324	0.3162	0.1	3.162
(0.1, 0.2)	(-0.4472, -0.3162) U (0.3162,0.4472)	0.2620	0.1310	0.1	1.310
(0.2, 0.3)	(-0.5477, -0.4472) U (0.4472,0.5477)	0.2010	0.1005	0.1	1.005
(0.3, 0.4)	(-0.6325, -0.5477) U (0.5477,0.6325)	0.1696	0.0848	0.1	0.848
(0.4, 0.5)	(-0.7071, -0.6325) U (0.6325,0.7071)	0.1492	0.0746	0.1	0.746
(0.5, 0.6)	(-0.7746, -0.7071) U (0.7071,0.7746)	0.1350	0.0675	0.1	0.675
(0.6, 0.7)	(-0.8367, -0.7746) U (0.7746,0.8367)	0.1242	0.0621	0.1	0.621
(0.7, 0.8)	(-0.8944, -0.8367) U (0.8367,0.8944)	0.1154	0.0577	0.1	0.577
(0.8, 0.9)	(-0.9487, -0.8944) U (0.8944,0.9487)	0.1086	0.0543	0.1	0.543
(0.9, 1)	(-1, -0.9487) U (0.9487,1)	0.1026	0.0513	0.1	0.513

We can use the table to sketch a histogram.

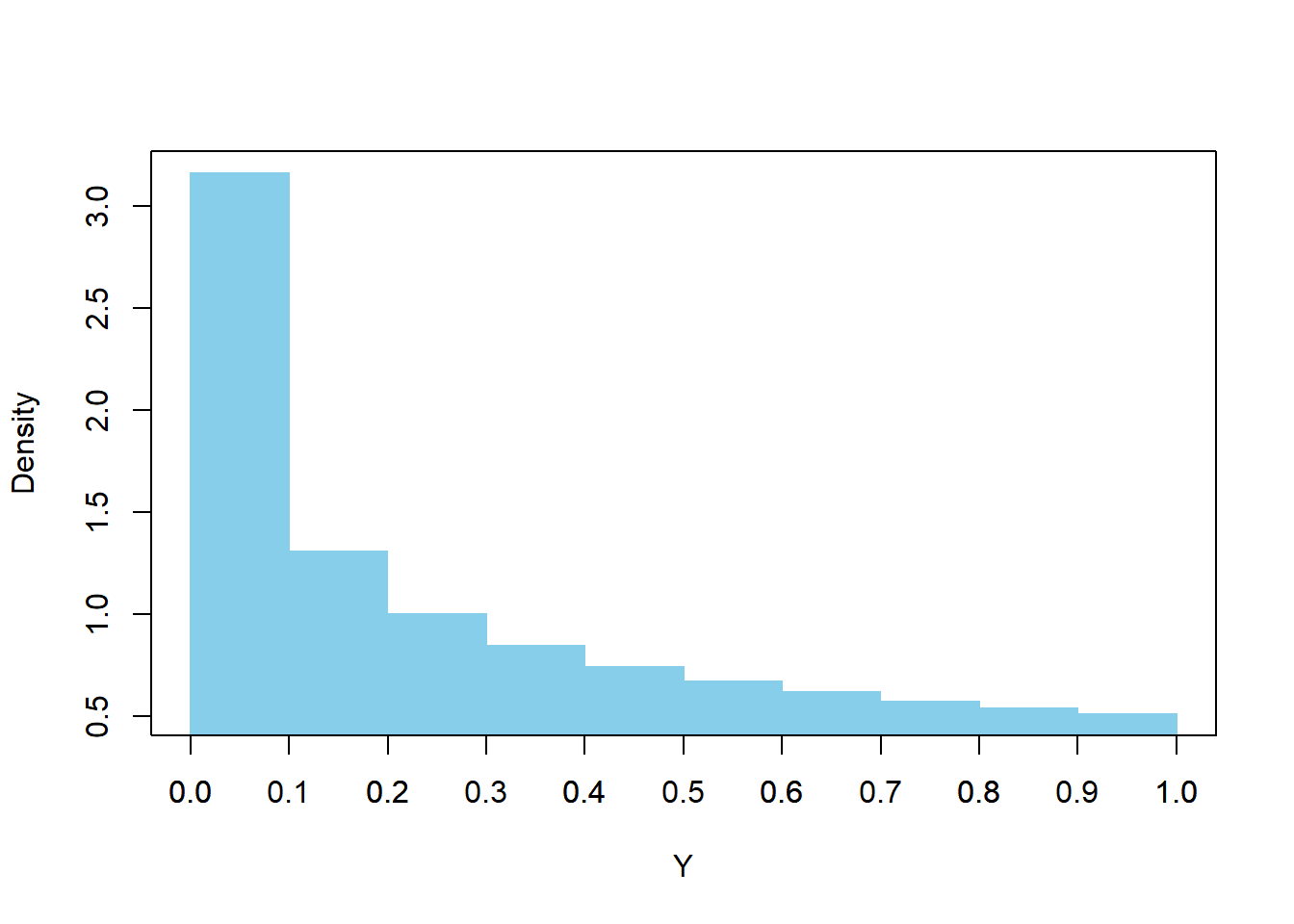
If we continued the above process with narrower and narrower $Y$ intervals we would arrive at the smooth pdf given by $f_Y(y) = \frac{1}{2\sqrt{y}}, 0<y<1$; see the black curve in the plot below.

Now we’ll approximate the pdf via simulation. The density blows up at 0 so it’s hard for the chunky histogram to capture that, but we see the simulated values follow a distribution described by the smooth $f_Y(y) = \frac{1}{2\sqrt{y}}, 0<y<1$ in the black curve.


X = RV(Uniform(-1, 1))
Y = X ** 2

plt.figure()

Y.sim(100000).plot()

# plot the density
from numpy import *
y = linspace(0.001, 1, 1000)
plt.plot(y, 0.5 / sqrt(y), 'k-');
plt.ylim(0, 10);

plt.show()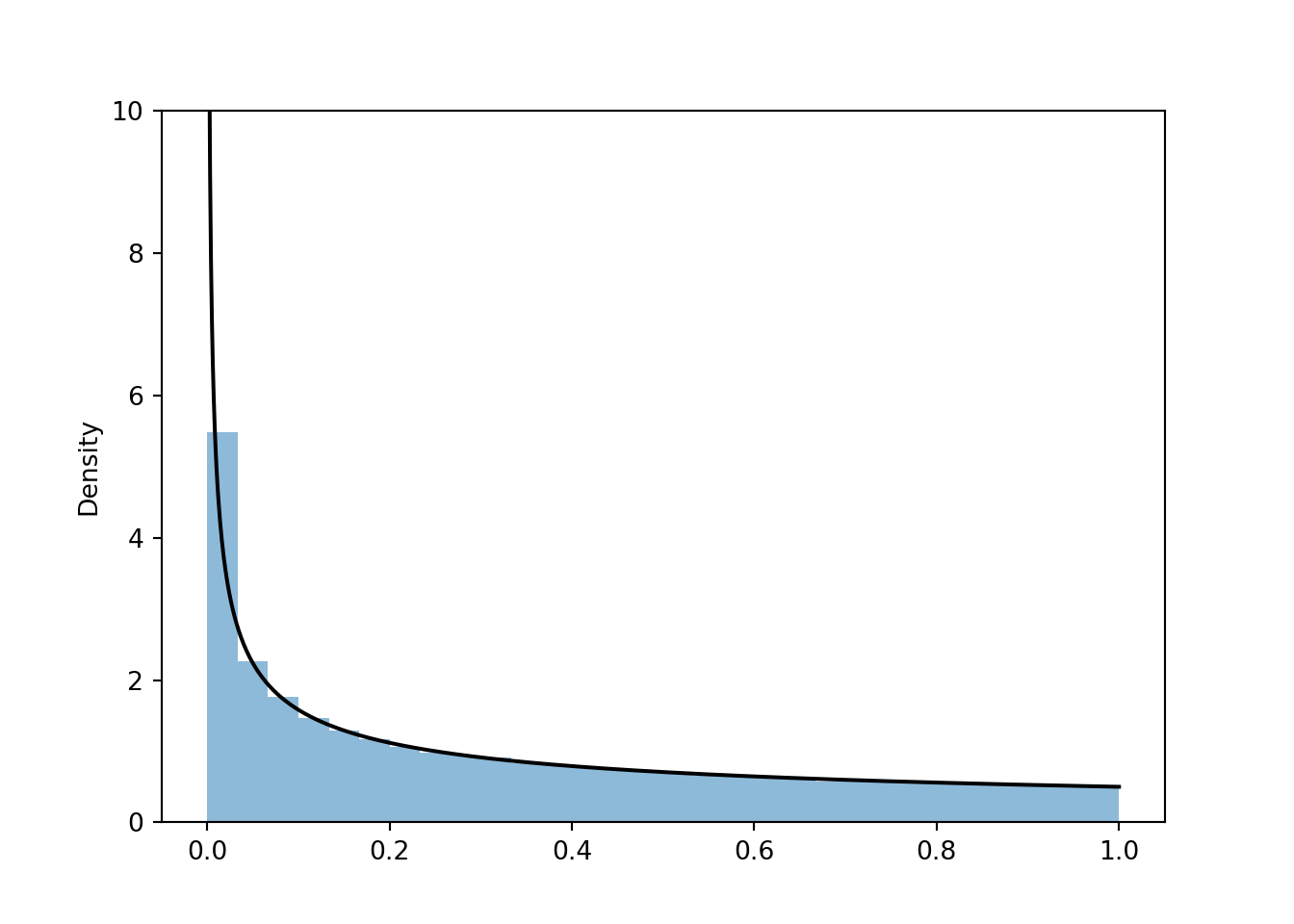

You might be familiar with “$mx+b$” where $b$ denotes the intercept. In Statistics, $b$ is often used to denote slope. For example, in R abline(a = 32, b = 1.8) draws a line with intercept 32 and slope 1.8.↩︎
If the mean were not 0, multiplying a random variable by $-1$ reflects the mean about 0 too, and distances from the mean are unaffected. For example, suppose $X$ has mean 1 so a value of 5 is 4 units away from the mean of 1. Then $-X$ has mean -1; a value of $X$ of 5 yields a value of $-X$ of -5, which is 4 units away from the mean of -1.↩︎
As in many other contexts and programming languages, in this text any reference to logarithms or $\log$ refers to natural (base $e$) logarithms. In the instances we need to consider another base, we’ll make that explicit.↩︎

Interval of \(U\) values	Probability that \(U\) lies in the interval	Interval of \(X\) values	Probability that \(X\) lies in the interval
(0.0, 0.1)	0.1	(200, 260)	\(\frac{60}{600}\)
(0.9, 1.0)	0.1	(740, 800)	\(\frac{60}{600}\)
(0.0, 0.2)	0.2	(200, 320)	\(\frac{120}{600}\)