3.1 Multiplication rule

Recall that the definition of conditional probability, \[ \textrm{P}(A | B) = \frac{\textrm{P}(A\cap B)}{\textrm{P}(B)}, \] can be rearranged to obtain the multiplication rule:

\[\begin{align*} \textrm{P}(A \cap B) & = \textrm{P}(A|B)\textrm{P}(B)\\ & = \textrm{P}(B|A)\textrm{P}(A) \end{align*}\]

The multiplication rule says that you should think “multiply” when you see “and”. However, be careful about what you are multiplying: to find a joint probability you need an marginal (i.e., unconditional) probability and an appropriate conditional probability. You can condition either on \(A\) or on \(B\), provided you have the appropriate marginal probability; often, conditioning one way is easier than the other. Be careful: the multiplication rule does not say that \(\textrm{P}(A\cap B)\) is the same as \(\textrm{P}(A)\textrm{P}(B)\).

Generically, the multiplication rule says \[ \text{joint} = \text{conditional}\times\text{marginal} \]

The multiplication rule is useful in situations where conditional probabilities are easier to obtain directly than joint probabilities.

Example 3.1 A standard deck of playing cards has 52 cards, 13 cards (2 through 10, jack, king, queen, ace) in each of 4 suits (hearts, diamonds, clubs, spades). Shuffle a deck and deals cards one at a time without replacement.

  1. Find the probability that the first card dealt is a heart.
  2. If the first card dealt is a heart, determine the conditional probability that the second card is a heart.
  3. Find the probability that the first two cards dealt are hearts.
  4. Find the probability that the first two cards dealt are hearts and the third card dealt is a diamond.
  5. Shuffle the deck and deal cards one at a time until an ace is dealt, and then stop. Find the probability that more than 4 cards are dealt. (Hint: consider the first 4 cards dealt.)

Solution. to Example 3.1

Show/hide solution
  1. If the cards are well shuffled, then any of the cards in the deck is equally likely to be the first card dealt. There are 13 hearts out of 52 cards in the deck, so the probability that the first card is a heart is 13/52 = 1/4 = 0.25.
  2. If the first card dealt is a heart, there are 51 cards left in the deck, 12 of which are hearts (and all the remaining cards in the deck are equally likely to be the next one drawn). So the conditional probability that the second card is a heart given that the first card is a heart is 12/51 = 0.235.
  3. Use the multiplication rule: the probability the both cards are hearts is the product of the probability that the first card is a heart and the conditional probability that the second card is a heart given that the first card is a heart, (13/52)(12/51) = 0.0588. If we imagine 132600 repetitions (a convenient choice given these fractions), then we would expect the first card to be a heart in 33150=132600(13/52) repetitions, and among these 33150 repetitions we would expect the second card to be a heart in 7800=33150(12/51) repetitions, so the proportion of repetitions in which both cards are hearts is 7800/132600 = 0.0588.
  4. The third card adds a third “stage” but the multiplication rule extended naturally. The probability the first two cards dealt are hearts and the third card dealt is a diamond is (13/52)(12/51)(13/50)= 0.0153, the product of:
    • 13/52, the probability that the first card is a heart,
    • 12/51, the conditional probability that the second card is a heart given that the first card is a heart, and
    • 13/50, the conditional probability that the third card is a diamond given that the first two cards are hearts. (If the first two cards are hearts, then there are 50 cards remaining in the deck, of which 13 are diamonds.) Continuing the simulation from the previous part, among the 7800 repetitions in which the first two cards are hearts, we would expect the third card will be a diamond in 2028 = 7800(13/50) repetitions, so the proportion of repetitions in which the first two cards are hearts and the third is a diamond is 2028/132600 = 0.0153.
  5. The key is to recognize that in this scenario more than 4 cards are needed to obtain the first ace if and only if the first four cards dealt are not aces. The probability that the first 4 cards are not aces is \((48/52)(47/51)(46/50)(45/49) = 0.719\).

The multiplication rule extends naturally to more than two events (though the notation gets messy). For three events, we have

\[ \textrm{P}(A_1 \cap A_2 \cap A_3) = \textrm{P}(A_1)\textrm{P}(A_2|A_1)\textrm{P}(A_3|A_1\cap A_2) \]

And in general, \[ \textrm{P}(A_1\cap A_2 \cap A_3 \cap A_4 \cap \cdots) = \textrm{P}(A_1)\textrm{P}(A_2|A_1)\textrm{P}(A_3|A_1\cap A_2)\textrm{P}(A_4|A_1\cap A_2 \cap A_4)\cdots \]

The multiplication rule is useful for computing probabilities of events that can be broken down into component “stages” where conditional probabilities at each stage are readily available. At each stage, condition on the information about all previous stages.

Example 3.2 The birthday problem concerns the probability that at least two people in a group of \(n\) people have the same birthday87. Ignore multiple births and February 29 and assume that the other 365 days are all equally likely88.

  1. If \(n=30\), what do you think the probability that at least two people share a birthday is: 0-20%, 20-40%, 40-60%, 60-80%, 80-100%? How large do you think \(n\) needs to be in order for the probability that at least two people share a birthday to be larger than 0.5? Just make guesses before proceeding to calculations.
  2. Explain how, in principle, you could perform a tactile simulation to estimate the probability that at least two people have the same birthday when \(n=30\).
  3. Now consider \(n=3\) people, labeled 1, 2, and 3. What is the probability that persons 1 and 2 have different birthdays?
  4. What is the probability that persons 1, 2, and 3 all have different birthdays given that persons 1 and 2 have different birthdays?
  5. What is the probability that persons 1, 2, and 3 all have different birthdays?
  6. When \(n = 3\). What is the probability that at least two people share a birthday?
  7. For \(n=30\), find the probability that none of the people have the same birthday.
  8. For \(n=30\), find the probability that at least two people have the same birthday.
  9. Write a clearly worded sentence interpreting the probability in the previous part as a long run relative frequency.
  10. When \(n=30\), how much more likely than not is it for at least two people to have the same birthday?
  11. Provide an expression of the probability for a general \(n\) and find the smallest value of \(n\) for which the probability is over 0.5. (You can just try different values of \(n\).)
  12. When \(n=100\) the probability is about 0.9999997. If you are in a group of 100 people and no one shares your birthday, should you be surprised?

Solution. to Example 3.2

Show/hide solution

  1. Your guesses are whatever they are. But many people who have never encountered this problem before say that the probability is 0-20%, and it takes \(n\) over at least 100 to get to a probability greater than 0.5.

  2. Here is one way.

    • Get 365 cards and label each one with a distinct birthday.
    • Shuffle the cards and select 30 with replacement.
    • Record whether or not you selected at least one card more than once. This corresponds to at least two people sharing a birthday.
    • Repeat many times; each repetition consists of selecting a sample of 30 cards with replacement.
    • Find the proportion of repetitions on which at least two people had the same birthday to approximate the probability.

    In the simulation below, the random variable \(X\) measures the number of distinct birthdays among the 30 people. So if no one shares a birthday then \(X=30\), if exactly two people share a birthday then \(X=29\), and so on.

  3. Whatever person 1’s birthday is, the probability that person 2 has the same birthday89 is 1/365, so the probability that person 2 has a different birthday than person 1 is 364/365.

  4. Given that person 1 and person 2 are born on different days, the probability that person 3 is also born on a different day is 363/365. (Notice the importance of the conditioning; if persons 1 and 2 share the same birthday, then the probability that person 3 is born on a different day is 364/365.)

  5. Use the multiplication rule: \((364/365)(363/365) = 0.992\), the probability that all three are born on different days, is the product of the probability that persons 1 and 2 are born on different days, and the conditional probability that person 3 is also born on a different day given that the first two are.

  6. Exactly one of the following must be true: (1) all 3 people are born on different days, or (2) at least two people share a birthday. Use the complement rule: when \(n=3\), the probability that at least two people share a birthday is \(1-(364/365)(363/365) = 0.008\).

  7. We can use the method for \(n=3\). Imagine lining the 30 people up in some order. Let \(A_2\) be the event that the first two people have different birthdays, \(A_3\) be the event that the first three people have different birthdays, and so on, until \(A_{30}\), the event that all 30 people have different birthdays. Notice \(A_{30}\subseteq A_{29} \subseteq \cdots \subseteq A_3 \subseteq A_2\), so \(\textrm{P}(A_{30}) = \textrm{P}(A_2 \cap A_3 \cap \cdots \cap A_{30})\).

    The first person’s birthday can be any one of 365 days. In order for the second person’s birthday to be different, it needs to be on one of the remaining 364 days. So the probability that the second person’s birthday is different from the first is \(\textrm{P}(A_2)=\frac{364}{365}\).

    Now if the first two people have different birthdays, in order for the third person’s birthday to be different it must be on one of the remaining 363 days. So \(\textrm{P}(A_3|A_2) = \frac{363}{365}\). Notice that this is a conditional probability. (If the first two people had the same birthday, then the probability that the third person’s birthday is different would be \(\frac{364}{365}\).)

    If the first three people have different birthdays, in order for the fourth person’s birthday to be different it must be on one of the remaining 362 days. So \(\textrm{P}(A_4|A_2\cap A_3) = \frac{362}{365}\).

    And so on. If the first 29 people have different birthdays, in order for the 30th person’s birthday to be different it must be on one of the remaining 365-29=336 days. Then using the multiplication rule

    \[\begin{align*} \textrm{P}(A_{30}) & = \textrm{P}(A_{2}\cap A_3 \cap \cdots \cap A_{30})\\ & = \textrm{P}(A_2)\textrm{P}(A_3|A_2)\textrm{P}(A_4|A_2\cap A_3)\textrm{P}(A_5|A_2\cap A_3 \cap A_4)\cdots \textrm{P}(A_{30}|A_2\cap \cdots \cap A_{29})\\ & = \left(\frac{364}{365}\right)\left(\frac{363}{365}\right)\left(\frac{362}{365}\right)\left(\frac{361}{365}\right)\cdots \left(\frac{365-30 + 1}{365}\right)\approx 0.294 \end{align*}\]

  8. By the complement rule, the probability that at least two people have the same birthday is \(1-0.294=0.706\), since either (1) none of the people have the same birthday, or (2) at least two of the people have the same birthday.

  9. In about 70% of groups of 30 people at least two people in the group will have the same birthday. For example, if Cal Poly classes all have 30 students, then in about 70% of your classes at least two people in the class will share a birthday.

  10. \(0.706 / 0.294 = 2.4.\) In a group of \(n=30\) people it is about 2.4 times more likely to have at least two people with the same birthday than not.

  11. For a general \(n\), the probability that at least two people have the same birthday is \[ 1 - \left(\frac{364}{365}\right)\left(\frac{363}{365}\right)\left(\frac{362}{365}\right)\left(\frac{361}{365}\right)\cdots \left(\frac{365-n + 1}{365}\right) \] See the plot below, which plots this probability as a function of \(n\). When \(n=23\) this probability is 0.507.

  12. Maybe, but not because of the 0.999997. That probability is the probability that at least two people in the group of 100 share a birthday. It is NOT the probability that someone shares YOUR birthday. (We will see later how to compute the probability that no one shares your birthday as \((364/365)^{100}= 0.76\). So it’s not very surprising that no one shares your birthday.)

def count_distinct_values(list):
    return len(set(list))
    
n = 30
P = BoxModel(list(range(365)), size = n, replace = True)
X = RV(P, count_distinct_values)

x = X.sim(10000)
x.plot()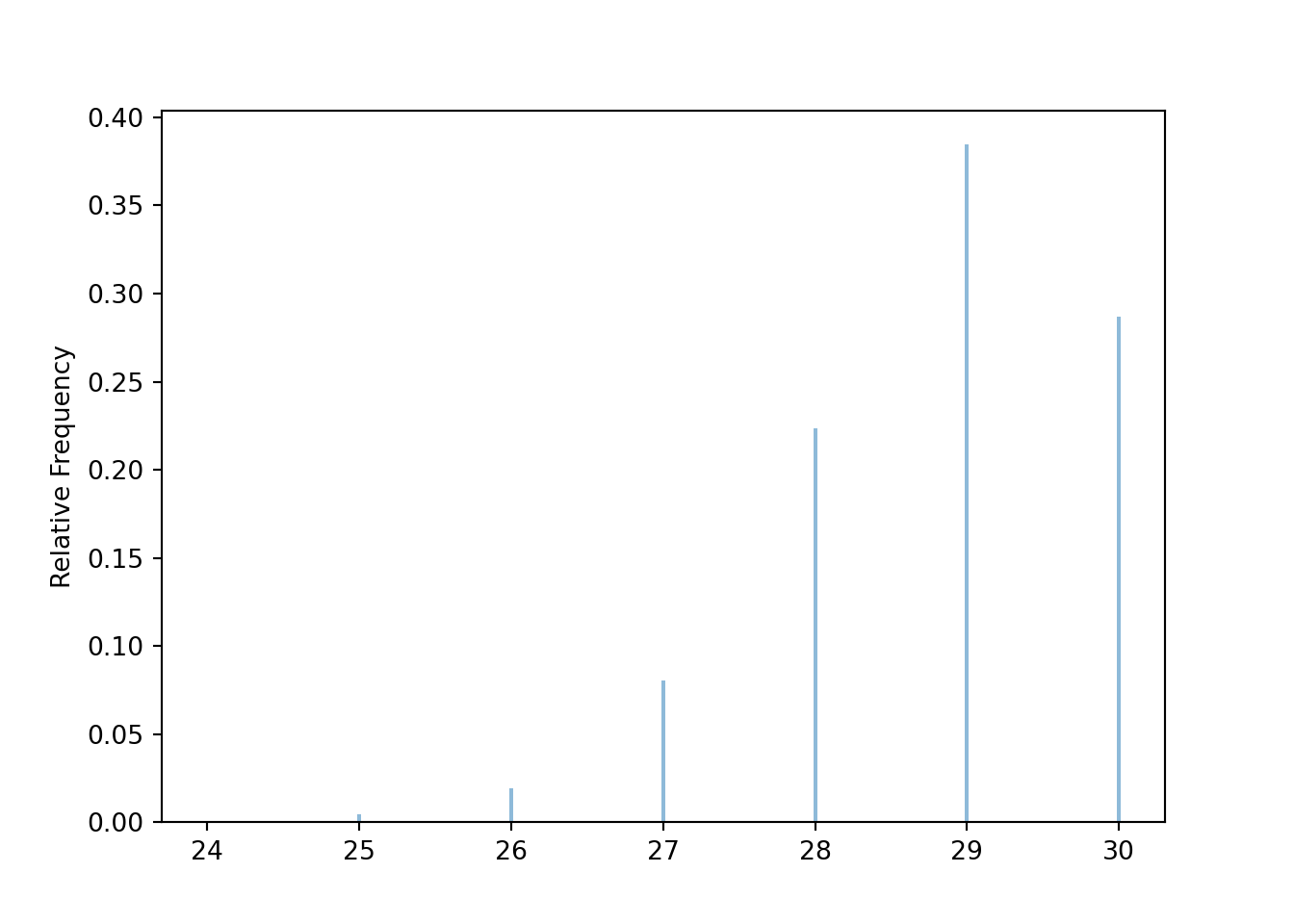


x.count_lt(n) / 10000
## 0.7133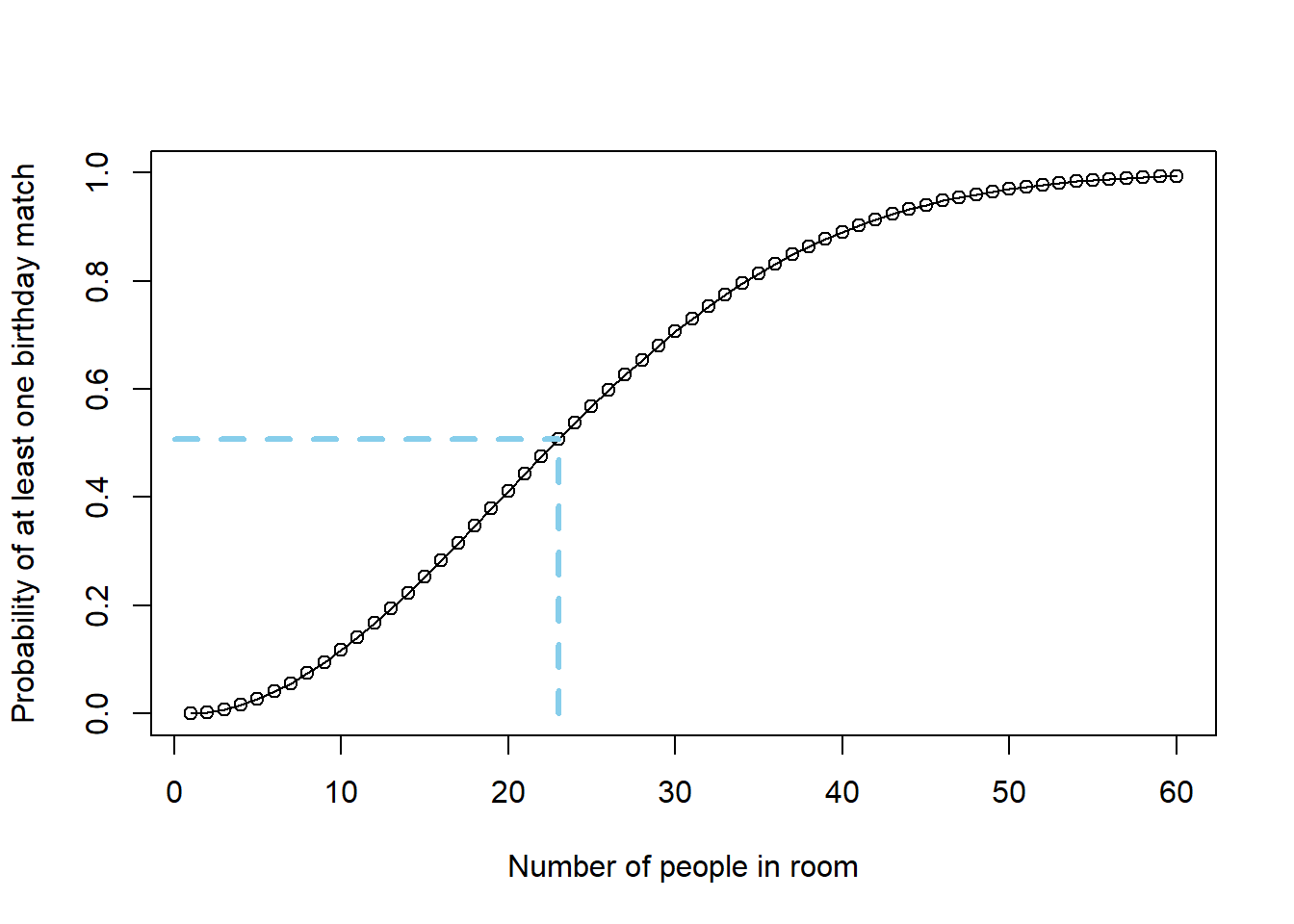
Probability of at least one birthday match as a function of the number of people in the room. For 23 people, the probability of at least one birthday match is 0.507.

Figure 3.1: Probability of at least one birthday match as a function of the number of people in the room. For 23 people, the probability of at least one birthday match is 0.507.

That only 23 people are needed to have a better than 50% chance of a birthday match is surprising to many people, because 23 doesn’t seem like a lot of people. But when determining if there is a birthday match, we need to consider every pair of people in the group. In a group of 23 people, there are \(23(22)/2 = 253\) different pairs of people, and each one of these pairs has a chance of sharing a birthday.

  1. You should really click on this birthday problem link.↩︎

  2. Which isn’t quite true. However, a non-uniform distribution of birthdays only increases the probability that at least two people have the same birthday. To see that, think of an extreme case like if everyone were born in September.↩︎

  3. Sometimes students mistake this for \((1/365)^2\); \((1/365)^2\) would be the probability that person 1 and person 2 both have a particular birthday, like January 1. There are \(365^2\) possible (person 1, person 2) birthday pairs, of which 365 — (Jan 1, Jan 1), (Jan 2, Jan 2), etc — result in the same birthday, so the probability of sharing a birthday is \(365/365^2 = 1/365\).) ↩︎