3.6 Equally likely outcomes
In this section we’ll look more closely at how to compute probabilities when the outcomes in the sample space are equally likely. But a warning before proceeding: in most situations sample space outcomes are not equally likely! And even in case where the outcomes are equally, values of corresponding random variables are usually not. So beware that the results in this section only apply in a limited number of special cases.
For a sample space \(\Omega\) with finitely many possible outcomes, assuming equally likely outcomes corresponds to a probability measure \(\textrm{P}\) which satisfies
\[ \textrm{P}(A) = \frac{|A|}{|\Omega|} = \frac{\text{number of outcomes in $A$}}{\text{number of outcomes in $\Omega$}} \qquad{\text{when outcomes are equally likely}} \]
Example 3.19 Flip a coin 4 times and record the results in sequence. For example, HTHH indicates T on the second flip and H on the others. Let \(X\) be the number of H in the four flips. Assume that the coin is fair and the flips are independent.
- Find the probability of the outcome HTHH.
- Find the probability of the outcome HHHH.
- Make a table of all the possible outcomes; there should be 16. Is it reasonable to assume the outcomes are equally likely? Explain.
- Identify the possible values of \(X\). Are the values of \(X\) equally likely?
- Compute and interpret \(\textrm{P}(X = 4)\).
- Compute and interpret \(\textrm{P}(X=3)\).
- Find the distribution of \(X\).
- Suppose the coin were biased in favor of landing on H. Would the sample space change? Would the definition of \(X\) and its possible values change? Would the 16 outcomes be equally likely? Would the distribution of \(X\) change?
Solution. to Example 3.19
Show/hide solution
- Since the coin is fair, the probability of H on any single flip is 0.5, same as the probability of T. Since the flips are independent, we can find the probability of the sequence by multiplying the probability of H/T for each flip. The probability of HTHH is (0.5)(0.5)(0.5)(0.5) = 0.0625 = 1/16.
- Similar to the previous part, the probability of H is 1/16.
- See Table 3.1. Assuming that the flips are independent and the coin is fair is equivalent to assuming that the probability of any single outcome is 1/16. So yes, it is reasonable to assume equally likely outcomes given these assumptions.
- \(X\) can take values 0, 1, 2, 3, 4. (Don’t forget 0.) Even though the 16 possible sequences are equally likely, the values of \(X\) are not. For example, there are more outcomes that result in \(X=3\) than \(X=4\).
- \(\textrm{P}(X = 4) = 1/16\) since there are 4 H in 4 flips if and only every flip is H, \(\{X = 4\} = \{HHHH\}\). Over many sets of 4 fair coin flips, about 6.25% of sets will result in 4 H. If you flip a coin 4 times, it is 15 times more likely to obtain fewer than 4 H than to obtain 4 H.
- \(\textrm{P}(X = 3) = 4/16\) since there are 4 outcomes (out of 16 equally likely outcomes) with 3 H in 4 flips, \(\{X = 3\} = \{HHHT, HHTH, HTHH, THHH\}\). Over many sets of 4 fair coin flips, about 25% of sets will result in exactly 3 H. If you flip a coin 4 times, it is 3 times more likely to obtain something other than 3 H than to obtain 3 H.
- The distribution can be represented in a table with the possible values \(x\) of \(X\), and \(\textrm{P}(X = x)\) for each possible \(x\). Since outcomes are equally, \(\textrm{P}(X = x)\) is the number of outcomes that satisfy the event \(\{X=x\}\) divided by 16, the total number of possible outcomes. See Table 3.2 and Figure 3.3.
- If the coin were biased in favor of landing on H, the sample space wouldn’t change; there would still be 16 possible flip sequences. The definition of \(X\) and its possible values also would not change. However, the 16 outcomes would no longer be equally likely. For example, the probability of HHHH would be greater than that of TTTT The distribution of \(X\) would also change; for example, \(\textrm{P}(X = 4)\) would be greater than 1/16$ and \(\textrm{P}(X = 0)\) would be less than 1/16.
| Outcome | X |
|---|---|
| HHHH | 4 |
| HHHT | 3 |
| HHTH | 3 |
| HTHH | 3 |
| THHH | 3 |
| HHTT | 2 |
| HTHT | 2 |
| HTTH | 2 |
| THHT | 2 |
| THTH | 2 |
| TTHH | 2 |
| HTTT | 1 |
| THTT | 1 |
| TTHT | 1 |
| TTTH | 1 |
| TTTT | 0 |
| x | P(X=x) |
|---|---|
| 0 | 0.0625 |
| 1 | 0.2500 |
| 2 | 0.3750 |
| 3 | 0.2500 |
| 4 | 0.0625 |
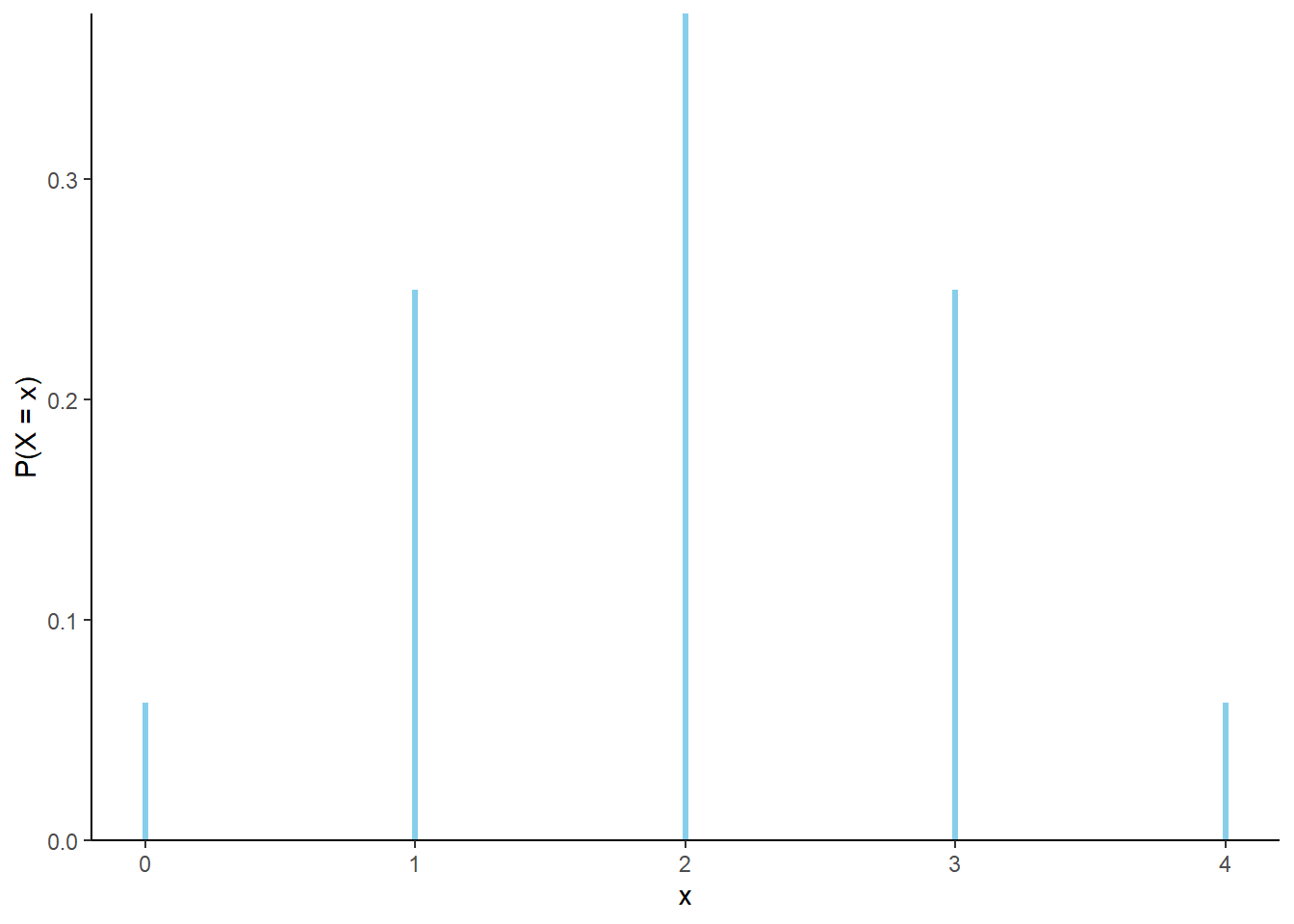
Figure 3.3: The marginal distribution of \(X\), the number of H in 4 flips of a fair coin.
Remember that events often involve random variables. Even if the sample space outcomes are equally likely, the possible values of related random variables are usually not.
Example 3.20 Recall the matching problem with \(n=4\): objects labeled 1, 2, 3, 4, are placed at random in spots labeled 1, 2, 3, 4, with spot 1 the correct spot for object 1, etc. Recall the sample space from Example 2.5. Let the random variable \(X\) count the number of objects that are put back in the correct spot. (Hint: recall Table 2.6.) Let \(\textrm{P}\) denote the probability measure corresponding to the assumption that the objects are equally likely to be placed in any spot, so that the 24 possible placements are equally.
- Find \(\textrm{P}(X=0)\).
- Find the distribution of \(X\).
- Let \(C\) be the event that at least one object is put in the correct spot. Compute and interpret \(\textrm{P}(C)\).
- Let \(C_1\) be the event that object 1 is put correctly in spot 1. Find \(\textrm{P}(C_1)\).
- Let \(C_2\) be the event that object 2 is put correctly in spot 2. Find \(\textrm{P}(C_2)\).
- Define \(C_3\), and \(C_4\) similarly. Represent the event \(C\) in terms of \(C_1, C_2, C_3, C_4\).
- Find and interpret \(\textrm{P}(C_1\cap C_2 \cap C_3 \cap C_4)\).
- Donny Don’t says: “the events are not disjoint so by the general addition rule \(\textrm{P}(C_1 \cup C_2 \cup C_3 \cup C_4)\) is equal to \(\textrm{P}(C_1)+\textrm{P}(C_2)+\textrm{P}(C_3)+\textrm{P}(C_4)-\textrm{P}(C_1\cap C_2 \cap C_3 \cap C_4)\).” Explain to Donny his mistake.
Solution. to Example 3.20
Show/hide solution
- Each of the 24 outcomes in Table 2.6 is equally likely. There are 9 outcomes for which \(Y=0\), so \(\textrm{P}(X=0)=9/24=0.375\).
- The possible values of \(X\) are 0, 1, 2, 4. \(X\) cannot be 3, since if 3 objects are in the correct spot, then the fourth must be too. \(\textrm{P}(X=x)\) for \(x=0, 1, 2, 4\) can be found as in the previous part. See Table 3.3 and Figure 3.4.
- \(C=\{X\ge 1\}\) is the event that at least one object is put in the correct spot. \(\textrm{P}(X \ge 1) = 1-\textrm{P}(X=0)=1-9/24 = 15/24 = 0.625\). If we were to repeat this process many times, with each repetition consisting of a placement of objects in spots, then about 62.5% of placements would have at least one object in the correct spot. \(\textrm{P}(C) = 0.625\) and \(\textrm{P}(C^c) = 0.375\), so it is about 1.67 times more likely to have at least one object in the correct spot than to have none.
- Intuitively, \(\textrm{P}(C_1)=1/4\) since object 1 is equally likely to be put in any of the 4 spots. In terms of the sample space outcomes, \(C_1 =\{1234, 1234, 1243, 1324, 1342, 1423, 1432\}\), so \(\textrm{P}(C_1)=6/24=1/4\).
- Similar to the previous part, \(\textrm{P}(C_2)=1/4\). Also, recalling the indicator random variables from Example 2.11, \(C_2=\{I_2=1\}\), and we see that there are 6 outcomes (rows) in Table 2.6 corresponding to \(I_2=1\). Similarly, \(\textrm{P}(C_3)=\textrm{P}(C_4)=1/4\).
- \(C = C_1\cup C_2\cup C_3\cup C_4\).
- \(\textrm{P}(C_1\cap C_2 \cap C_3 \cap C_4) = \textrm{P}(\{1234\}) = 1/24\) is the probability that all four objects are put in their correct spots.
- As we mentioned previously, the general addition rule is complicated for more than two events. There are some terms missing from Donny’s calculation.
| x | P(X=x) |
|---|---|
| 0 | 0.3750 |
| 1 | 0.3333 |
| 2 | 0.2500 |
| 4 | 0.0417 |
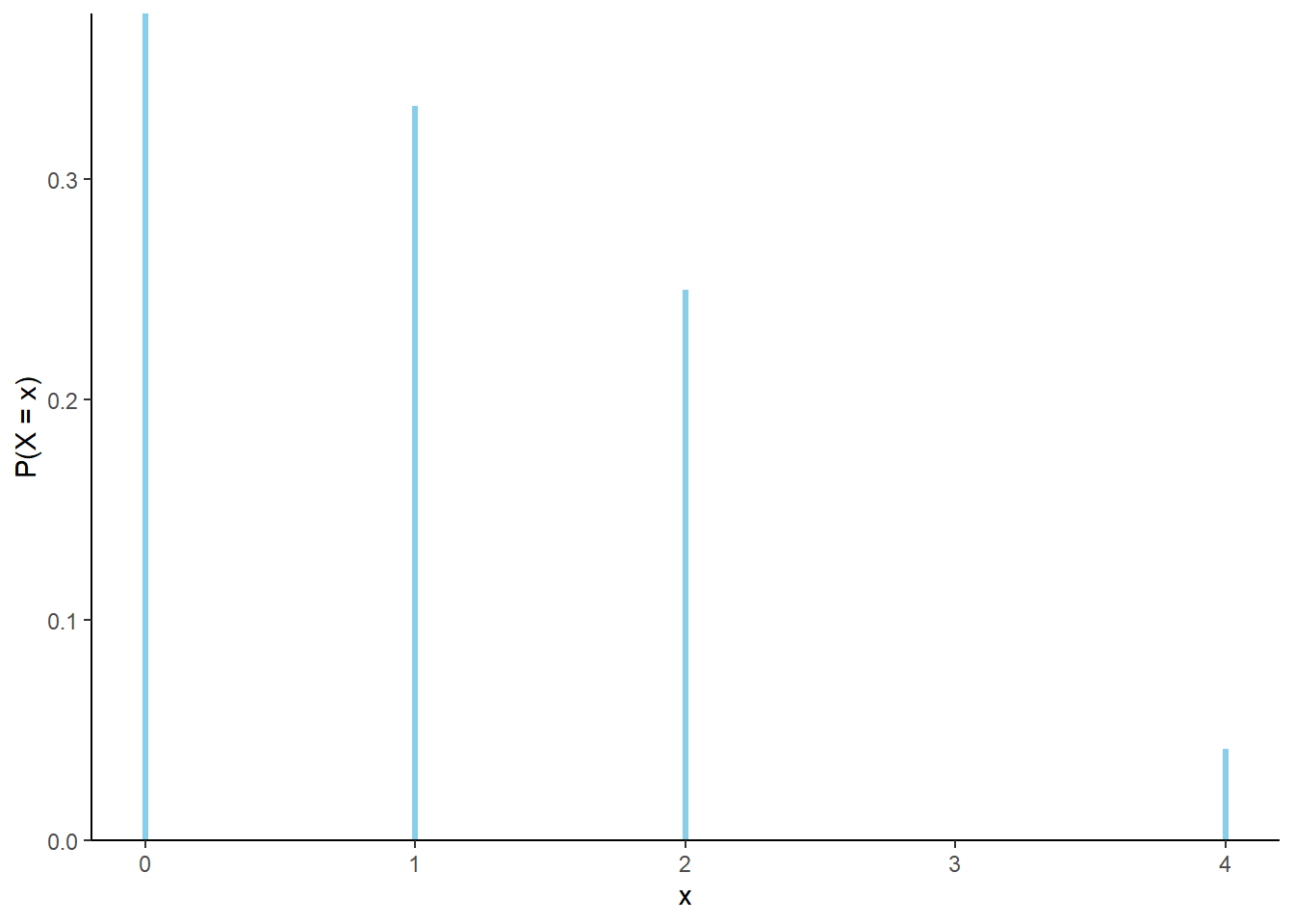
Figure 3.4: Distribution of \(X\), the number of matches in the matching problem with \(n=4\) and uniformly random placement of objects in spots.
The last part of Example 3.20 is a reminder that the general addition rule for multiple events is complicated and not very useful. Remember that it is usually more convenient to use the complement rule and compute “the probability of at least one…” as one minus “the probability of none…”; the latter probability involves intersections and is an “and” event.
3.6.1 Some counting rules
Computing probabilities in the equally likely case reduces to just counting outcomes. In previous sections we often counted outcomes by enumerating them in a list. Of course, listing all the outcomes is unfeasible unless the sample space is very small. In this section we will see some formulas for counting in a few common situations.
Example 3.21 I’m serving ice cream to my kids. They can choose to have a bowl or a cone with a single scoop from one of four different flavors.
- How many different ways could I serve the ice cream? (For example, peppermint in a cone, birthday cake in a bowl, etc)
- Now suppose they can either add rainbow or chocolate sprinkles97 or not. How many different ways could I serve the ice cream? (For example, peppermint in a cone with chocolate sprinkles, birthday cake in a bowl with rainbow sprinkles, etc.)
- Now suppose the kids who requested bowls could choose whether to have whipped cream on top. Is the number of different ways I could serve the ice cream equal to the answer to the previous part multiplied by two?
Solution. to Example 3.21
Show/hide solution
- Each flavor can be served in 2 ways, cone or bowl. Since there are 4 flavors, the number of ways to serve is \(4\times 2 = 8\).
- Each of the 8 pairs from the previous part can be served in 3 ways, with rainbow sprinkles, with chocolate sprinkles, or without sprinkles. So the number of ways to serve is now \(4\times 2 \times 3 = 24\).
- No. Only the bowls can get whipped cream so we can’t just multiply 24 by 2. Of the 24 possibilities from the previous part, 12 are in bowls. So these 12 can be served with or without whipped cream, but the other 12 in cones can only be served without whipped cream. The number of possibilities is now \(12\times 2 + 12 = 36\).
All of the counting rules we will see are based on multiplying like in the previous example.
Multiplication principle for counting. Suppose that stage 1 of a process can be completed in any one of \(n_1\) ways. Further, suppose that for each way of completing the stage 1, stage 2 can be completed in any one of \(n_2\) ways. Then the two-stage process can be completed in any one of \(n_1\times n_2\) ways. This rule extends naturally to a \(\ell\)-stage process, which can then be completed in any one of \(n_1\times n_2\times n_3\times\cdots\times n_\ell\) ways.
In the multiplication principle it is not important whether there is a “first” or “second” stage. What is important is that there are distinct stages, each with its own number of “choices”. In Example 3.21, there was a bowl/cone stage, an ice cream flavor stage, and a sprinkle stage.
Example 3.22 Use the multiplcation rule to verify the total number of possible outcomes for a few of the examples we have seen previously. (In many of these situations we counted the total number of outcomes by listing them all.)
- 16 possible outcomes when rolling a four-sided die twice
- 36 possible outcomes when rolling a six-sided die twice
- 16 possible outcomes when flipping a coin 4 times.
- 24 possible outcomes in the matching problem with \(n=4\).
Solution. to Example 3.22.
Show/hide solution
- An outcome is a pair (first roll, second roll). There are 4 possibilities for the first roll and 4 for the second, so \(4\times4 = 16\) possible pairs.
- Similarly to the previous part: \(6\times 6=36\) possible outcomes.
- An outcome is a sequence of the H/T results of each of the 4 flips. There are two possibilities for each flip, so \((2)(2)(2)(2) = 2^4=16\) possible outcomes.
- There are 4 possibilities for the object placed in spot 1. After placing that object, there are 3 possibilities for spot 2, then 2 possibilities for spot 3, with one object left for spot 4. So there are \(4\times3\times2\times1 = 24\) possible arrangements.
Example 3.23 Suppose the board of directors of a corporation has identified 5 candidates — Ariana, Beyonce, Cardi, Drake, Elvis — for three executive positions: chief executive officer (CEO), chief financial officer (CFO), and chief operating officer (COO). In the interest of fairness, the board assigns 3 of the 5 candidates to the positions completely at random. No individual can hold more than one of the positions.
When calculating probabilities below, consider the sample space of all possible executive teams.
- How many executive teams are possible?
- What is the probability that Ariana is CEO, Beyonce is CFO, and Cardi is COO?
- What is the probability that Ariana is CEO, Cardi is CFO, and Beyonce is COO?
- What is the probability that Ariana is CEO and Beyonce is CFO?
- What is the probability that Ariana is CEO?
- What is the probability that Ariana is an executive?
Solution. to Example 3.23
Show/hide solution
- There are 5 choices for CEO, then 4 choices for CFO, then 3 choices for COO. So there are \(5\times 4 \times 3 = 60\) possible teams. The sample space consists of 60 possible outcomes. The order in which we make the choices doesn’t matter. We could have picked the CFO first then COO then CEO, still resulting in \(5\times 4\times3\) possible outcomes. What is important is that there are 3 distinct stages. Choosing Ariana as CEO is not the same as choosing Ariana as CFO.
- If the selections are made uniformly at random, each of the 60 possible teams is equally likely. So the probability of any particular team, like this one, is 1/60.
- The probability of any particular team is 1/60. But note that Ariana as CEO, Beyonce as CFO, and Cardi as COO is a different outcome than Ariana as CEO, Cardi as CFO, and Beyonce as COO
- To construct a team with Ariana as CEO and Beyonce as CFO, there is one possible choice for CEO (Ariana), one possible choice for CFO (Beyonce) and three possible choices for COO, resulting in \(1\times 1\times 3\) teams that have Ariana as CEO and Beyonce as CFO. Since the outcomes are equally likely, the probability is 3/60.
- To construct a team with Ariana as CEO, there is one possible choice for CEO (Ariana), four possible choicea for CFO, and three possible choices for COO, resulting in \(1\times 4\times 3=12\) teams that have Ariana as CEO. Since the outcomes are equally likely, the probability is 12/60=1/5. This makes sense because any of the five people is equally likely to be CEO.
- The probability that Ariana is CEO is 12/60, similarly for CFO and COO. Since Ariana can’t hold more than one positive, these events are disjoint, so the probability that Ariana is CEO or CFO or COO is \(3(12/60) = 3/5\).
Here are just 10 of the 60 possible executive teams
| CEO | CFO | COO |
|---|---|---|
| A | B | C |
| A | C | B |
| B | A | C |
| B | C | A |
| C | A | B |
| C | B | A |
| A | B | D |
| A | B | E |
| A | C | D |
| A | C | E |
In the previous example, the “stage” at which the person was chosen was important: there was a CEO stage, a CFO stage, and a COO stage. Choosing Ariana at the CEO stage, Beyonce at the CFO stage, and Cardi at the COO stage was a different outcome than choosing Ariana at the CEO stage, Cardi at the CFO stage, and Beyonce at the COO stage. When what happens at each stage matters, an outcome is often called an “ordered” arrangement. Again, “order” is perhaps a misnomer; it’s not that there’s a “first” and “second” and “third” stage, but rather that there are three distinct stages — CEO, CFO, COO.
The multiplication principle applies directly to situations which involve “ordered” or stage-wise counting, like the executive example. We employed the multiplication principle to find that there are \(5\times 4\times 3=60\) possible executive teams. The following formula generalizes this result.
Number of ordered arrangements. The number of ordered arrangements of \(k\) items, selected without replacement from a set of \(n\) distinct items is \[ n(n-1)(n-2)\cdots(n-k+1) = \frac{n!}{(n-k)!} \]
Recall the factorial notation: \(m!=m(m-1)(m-2)\cdots (3)(2)(1)\). For example, \(5!=5\times4\times3\times2\times1=120\). By definition, 0!=1.
Example 3.24 Your boss is forming a committee of 3 people for a new project team, and 5 people — Ariana, Beyonce, Cardi, Drake, Elvis— have volunteered to be on the committee. In the interest of fairness, 3 of the 5 people will be selected uniformly at random to form the committee.
- How is this situation different from the executive team example?
- How many possible committees consist of Ariana, Beyonce, Cardi? How many executive teams consisted of Ariana, Beyonce, Cardi?
- How many different possible committees of 3 people can be formed from the 5 volunteers?
Solution. to Example 3.24
Show/hide solution
- There were distinct stages in the executive team example; selecting Ariana as CEO, Beyonce as CFO, and Cardi as COO was counted as a different outcome than selecting Ariana as CEO, Cardi as CFO, and Beyonce as COO. But when forming the committee we only need to know which three people were selected, not which stage or “order” they were selected in.
- There is only one committee that consists of Ariana, Beyonce, Cardi. But there were 6 executive teams that consisted of Ariana, Beyonce, Cardi. To have a team with these three people, there are 3 choices for who is CEO, then 2 choices for COO, then 1 choice for COO, for a total of \(3\times2\times1=6\) possible teams consisting of Ariana, Beyonce, Cardi.
- There were 60 possible “ordered” outcomes, but counting in an “ordered” way overcounts the number of committees by a factor of 6. Counting in an “ordered” way would count 6 teams consisting of Ariana, Beyonce, Cardi, but we only want to count the possible committee once. Therefore, the total number of committees is 60/6 = 10.
The following is the relationship between “ordered” and “unordered” counting.
\[ \scriptsize{ \begin{align*} \left(\text{number of \emph{ordered} selections of $k$ from $n$}\right) & = \left(\text{number of \emph{unordered} selections of $k$ from $n$}\right)\\ &\quad \times\left(\text{number of ways of arranging the $k$ items in order}\right). \end{align*} } \]
We have seen how to compute the number of “ordered” arrangements. How many ways are there of arranging \(k\) items in order?
Number of permutations. The number of ways of arranging \(k\) items in order is \[ k\times (k-1)\times (k-2)\times\cdots\times 3\times 2\times1 = k! \] This can be seen as an application of the multiplication rule, or as a special case of the number of “ordered” arrangements rule with \(n=k\). Permutation is another word for an ordering of \(k\) items.
Here are the 6 executive teams consisting of Ariana, Beyonce, and Cardi.
| CEO | CFO | COO |
|---|---|---|
| A | B | C |
| A | C | B |
| B | A | C |
| B | C | A |
| C | A | B |
| C | B | A |
We now have what we need to count the number of ordered arrangements. We know that the number of ordered arrangements is \(n!/(n-k)!\), that the number of ways of arranging the \(k\) items is \(k!\) and so using the relationship noted above, we must have that the number of unordered arrangements is \((n!/(n-k)!)/k!\). More precisely,
Number of combinations. The number of ways to choose \(k\) items without replacement from a group of \(n\) distinct items where order does not matter, denoted \(\binom{n}{k}\), is \[ \binom{n}{k} = \frac{n(n-1)(n-2)\cdots(n-k+1)}{k!} = \frac{n!}{k!(n-k)!} \]
The quantity on the right is just a compact way of representing the quantity in the middle. But since factorials can be very large, it’s best to use the quantity in the middle to compute. In R: choose(n, k). In Python: scipy.special.comb(n, k)
An unordered selection of \(k\) items from a group of \(n\) is sometimes called a combination, so \(\binom{n}{k}\) is sometimes called the number of combinations. The symbol \(\binom{n}{k}\) is by definition equal to the quantity in the middle above. It is read as “\(n\) choose \(k\)” and is referred to as a binomial coefficient. For example, there are “5 choose 3” committees in the previous example
\[ \binom{5}{3} = \frac{5!}{3!(5-3)!} = \frac{(5)(4)(3)}{3!} = \frac{60}{6} = 10. \]
Here are the 10 possible committes of 3 people.
| One person | Another person | One more person |
|---|---|---|
| A | B | C |
| A | B | D |
| A | B | E |
| A | C | D |
| A | C | E |
| A | D | E |
| B | C | D |
| B | C | E |
| B | D | E |
| C | D | E |
Example 3.25 Your boss is forming a committee of 3 people for a new project team, and 5 people — Ariana, Beyonce, Cardi, Drake, Elvis— have volunteered to be on the committee. In the interest of fairness, 3 of the 5 people will be selected uniformly at random to form the committee.
- Find the probability that the committee consists of Ariana, Beyonce, and Cardi.
- Find the probability that Ariana and Beyonce are on the committee.
- Find the probability that Ariana is on the committee.
Solution. to Example 3.25
Show/hide solution
- If the selections are made uniformly at random each of the \(\binom{5}{3} = 10\) possible committees is equally likely. So the probability of any particular committee, like this one, is 1/10.
- Split the five people into two groups: group 1 with Ariana and Beyonce and group 2 with the other three. In order to have a committee with Ariana and Beyonce, we need to choose 2 people from group 1 and 1 person from group 2. There is only way to choose the 2 people from group 1, and there are three possibilities for the person selected from group 2. Each of these three people can be partnered with Ariana and Beyonce to form the committee. Therefore, the probability is 3/10. Written another way \[ \frac{\binom{2}{2}\binom{3}{1}}{\binom{5}{3}} = \frac{(1)(3)}{10} \]
- Intuitively, this should be 3/5, the same as the probability that Ariana was an executive. Split the five people into two groups: group 1 with Ariana and group 2 with the other four. In order to have a committee with Ariana, we need to choose Ariana from group 1 and 2 people from group 2. There is only way to choose the Ariana from group 1, and there are \(\binom{4}{2}=6\) possibilities for the two people selected from group 2. Each of these pairs can be partnered with Ariana to form a committee with Ariana on it. Therefore, the probability is 6/10. Written another way \[ \frac{\binom{1}{1}\binom{4}{2}}{\binom{5}{3}} = \frac{(1)(6)}{10} \]
The strategy of partitioning is often useful in problems involving “unordered” sampling without replacement. Notice that in each of the problems above the denominator had one binomial coefficient, corresponding to the total number of selections. Then the totals were partitioned into some number of groups, determined by the event of interest. The numerator of the probability will have one binomial coefficient for each group; the sums of the “tops” of the binomial coefficients in the numerator will equal the top of the binomial coefficient in the denominator, and the the sums of the “bottoms” of the binomial coefficients in the numerator will equal the bottom of the binomial coefficient in the denominator.
Example 3.26 In the Powerball lottery, a player picks five different whole numbers between 1 and 69, and another whole number between 1 and 26 that is called the Powerball. In the drawing, the 5 numbers are drawn without replacement from a “hopper” with balls labeled 1 through 69, but the Powerball is drawn from a separate hopper with balls labeled 1 through 26. The player wins the jackpot if both the first 5 numbers match those drawn, in any order, and the Powerball is a match.
How many different possible winning draws are there?
Solution. to Example 3.26
Show/hide solution
There are \(\binom{69}{5}\) ways of choosing the 5 numbers from the 69, and each of these can be paired with one of the 26 possible Powerballs. Therefore, there are \(\binom{69}{5}(26) = 292,201,338\) possible winning numbers.
Example 3.27 To get some intuition behind binomial coefficients, answer the following without using any formulas or doing any calculations.
- What is \(\binom{n}{n}\)?
- What is \(\binom{n}{0}\)?
- What is \(\binom{n}{1}\)?
- What is the relationship between \(\binom{n}{k}\) and \(\binom{n}{n-k}\)?
- Explain why \[\begin{equation*} \binom{m+n}{k} = \sum_{j=0}^k \binom{m}{j} \binom{n}{k-j} \end{equation*}\]
- Explain why \[\begin{equation} 2^n = \sum_{k=0}^n\binom{n}{k} \end{equation}\]
Solution. to Example 3.27
Show/hide solution
- \(\binom{n}{n}=1\). There is only one way to select all \(n\) items.
- \(\binom{n}{0}=1\). There is only one way to select none of the \(n\) items.
- \(\binom{n}{1}=n\). If you are just selecting 1 of \(n\) items, then are \(n\) ways to do it, one for each of the \(n\) items.
- \(\binom{n}{k}=\binom{n}{n-k}\). Suppose you are selecting a committee of size \(k\) from \(n\) peoeple. The number of ways to choose \(k\) of the \(n\) people to include on the committee is equivalent to the number of ways to choose \(n-k\) of the \(n\) people to exclude from the committee.
- Suppose you are choosing a committee of size \(k\) from a group consisting of \(m\) faculty and \(n\) students. The left side \(\binom{m+n}{k}\) is the number of possible committees. There can be anywhere from 0 to \(k\) faculty on the committee. If there are \(j\) faculty there must be \(k-j\) students, so \(\binom{m}{j} \binom{n}{k-j}\) is the number of ways to select a committee with exactly \(j\) faculty. The right side sums the number of committees of each faculty/student breakdown to find the number of committees overall.
- Suppose you are forming a subset from \(n\) items. There are \(2^n\) possible subsets, including the empty set. This follows from the multiplication principle since each of the \(n\) items can either be included or excluded in the subset. (Label the items 1 to \(n\); at the “include item 1 in the subset?” stage there are two possible choices, etc, so the total number of choices is \(2^n\).) \(\binom{n}{k}\) is the number of subsets of size \(k\); sum the numbers of subsets of each size to get the overall number of subsets.
Example 3.28 Continuing Example 3.19.
- Use counting rules to find a formula for \(\textrm{P}(X = 3)\).
- Use counting rules to find a formula for \(\textrm{P}(X = 2)\).
- Use counting rules to find a formula for \(\textrm{P}(X = x)\) for each possible value of \(x\).
- Now suppose the coin is flipped \(n\) times. Continue to assume the coin is fair and the flips are independent. Let \(X\) count the number of H in \(n\) flips. Use counting rules to find a formula for \(\textrm{P}(X = x)\) for each possible value of \(x\).
Solution. to Example 3.28
Show/hide solution
- We need to count the number of outcomes with exactly 3 H. There are 4 “spots” in the sequence, and we need to choose 3 of them to put the H’s in, so there are \(\binom{4}{3} = 4\) ways to do so. So \(\textrm{P}(X = 3) = \binom{4}{3}/2^4 = 4/16\).
- We need to count the number of outcomes with exactly 2 H. There are 4 “spots” in the sequence, and we need to choose 2 of them to put the H’s in, so there are \(\binom{4}{2} = 6\) ways to do so. So \(\textrm{P}(X = 2) = \binom{4}{2}/2^4 = 6/16\).
- There are \(2^4\) equally likely outcomes. For \(X=x\) to be true, we need exactly \(x\) H. There are 4 “spots” in the sequence, and we need to choose \(x\) of them to put the H’s in, so there are \(\binom{4}{x}\) ways to do so. \[ \textrm{P}(X = x) = \frac{\binom{4}{x}}{2^4}, \qquad x = 0, 1, 2, 3, 4 \]
- There are \(n\) flips, each with two possibilities, so there are \(2^n\) equally likely coin flip sequences. The possible values of \(X\) are \(0, 1, 2, \ldots, n\). For \(X=x\) to be true, there are \(n\) spots in the sequence and we need to choose \(x\) of them to put the \(x\) H in, so there are \(\binom{n}{x}\) ways to do so. That is, \(\binom{n}{x}\) is the number of outcomes with exactly \(x\) H (out of the \(2^n\) equally likely outcomes). \[ \textrm{P}(X = x) = \frac{\binom{n}{x}}{2^n}, \qquad x = 0, 1, 2, \ldots, n \]