1.2 Interpretations of probability

In the previous section we encountered a variety of scenarios which involved uncertainty, a.k.a. randomness. Just as there are a few “types” of randomness, there are a few ways of interpreting probability, most notably, long run relative frequency and subjective probability.

1.2.1 Long run relative frequency

One of the oldest documented4 problems in probability is the following: If three fair six-sided dice are rolled, what is more likely: a sum of 9 or a sum of 10? Let’s try to answer this question by simply rolling dice and seeing if a sum of 9 or 10 happens more frequently. Roll three fair six-sided dice, find the sum, repeat many times, and see how often we get a sum of 9 versus a sum of 10. Table 1.1 displays the results of a few repetitions. We encourage you to try this out on your own now; of course, your results will naturally be different from ours.

Table 1.1: Results of 10 sets of three rolls of a fair six-sided die.
Repetition First roll Second roll Third roll Sum
1 3 6 3 12
2 1 2 4 7
3 4 2 4 10
4 2 2 1 5
5 4 6 1 11
6 5 1 2 8
7 3 1 3 7
8 5 5 6 16
9 5 6 3 14
10 4 5 2 11

The results of a few repetitions should not be very convincing. What we really want is to perform many, many repetitions. Of course, this would be a time consuming process by hand, but it’s quick and easy on a computer. Figure 1.2 displays the result of one million repetitions of this process, each repetition resulting in the sum of three rolls. A sum of 9 occurred in 115392 repetitions and a sum of 10 occurred in 125026 repetitions. Comparing these frequencies, our results suggest that a sum of 10 is more likely than a sum of 9.

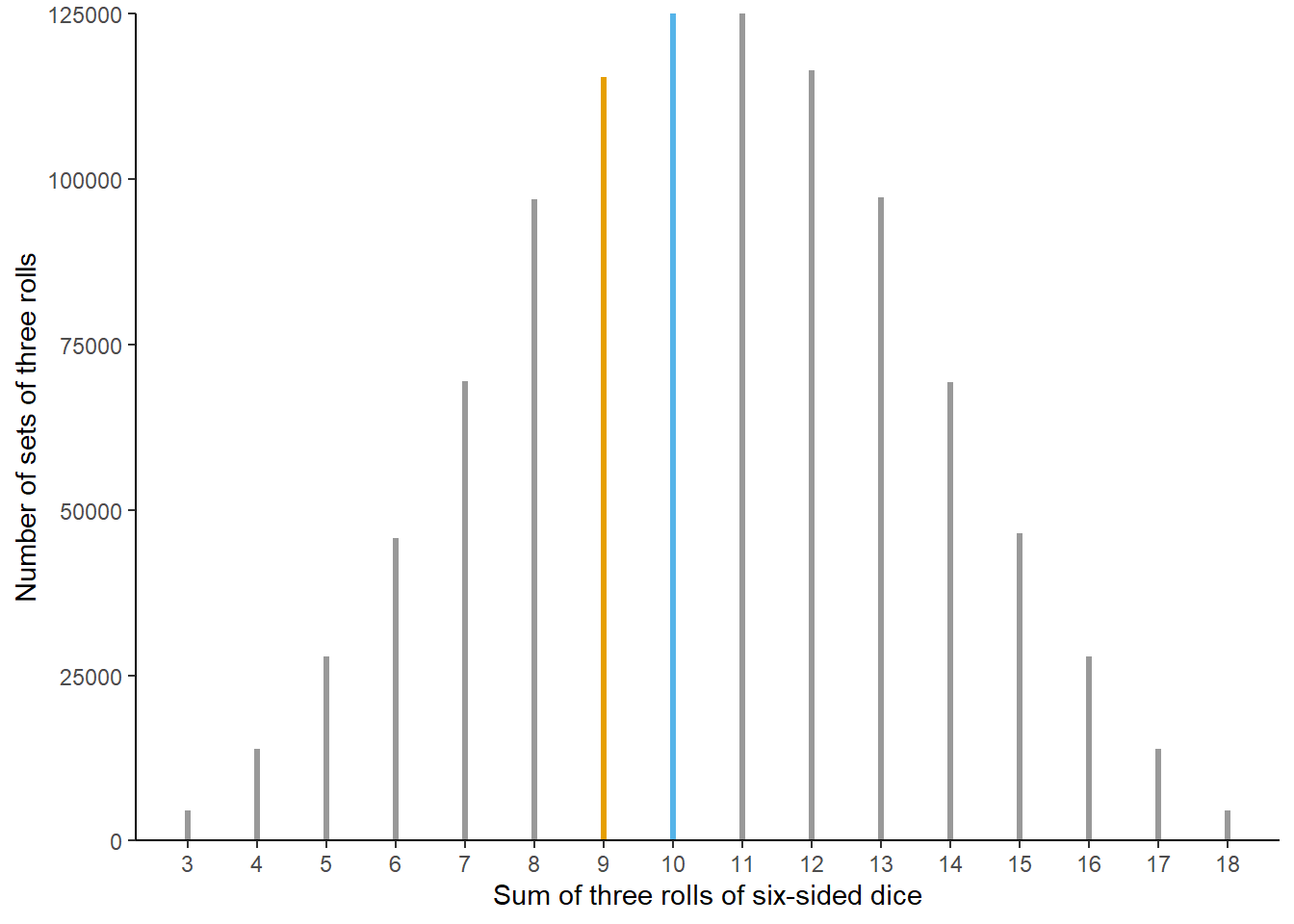
Results of 1 million sets of three rolls of fair six-sided dice. Sets in which the sum of the dice is 9 (10) are represented by orange (blue) spike.

Figure 1.2: Results of 1 million sets of three rolls of fair six-sided dice. Sets in which the sum of the dice is 9 (10) are represented by orange (blue) spike.

In the previous problem we assessed relative likelihoods by repeating the process many times. This is the idea behind the relative frequency interpretation of probability. We’ll investigate this idea further in the context of what is probably the most iconic random process: coin flipping.

We might all agree that the probability that a single flip of a fair coin lands on heads is 1/2, a.k.a., 0.5, a.k.a, 50%. After all, the notion of “fairness” implies that the two outcomes, heads and tails, should be equally likely, so we have a “50/50 chance” of heads. But how else can we interpret this 50%? As in the dice rolling problem, we can consider what would happen if we flipped the coin main times. Now, if we would flipped the coin twice, we wouldn’t expect to necessarily see one head and one tail. But in many flips, we might expect to see heads on something close to 50% of flips.

Let’s try this out. Table 1.2 displays the results of 10 flips of a fair coin. The first column is the flip number (first flip, second flip, and so on) and the second column is the result of the flip. The third column displays the running proportion of flips that result in H. For example, the first flip results in T so the running proportion of H after 1 flip is 0/1; the first two flips result in (T, H) so the running proportion of H after 2 flips is 1/2; the first three flips result in (T, H, H) so the running proportion of H after 2 flips is 2/3; and so on. Figure 1.3 plots the running proportion of H by the number of flips. We see that with just a small number of flips, the proportion of H fluctuates considerably and is not guaranteed to be close to 0.5. Of course, the results depend on the particular sequence of coin flips. We encourage you to flip a coin 10 times and compare your results.

Table 1.2: Results and running proportion of H for 10 flips of a fair coin.
Flip Result Running count of H Running proportion of H
1 T 0 0.000
2 H 1 0.500
3 H 2 0.667
4 H 3 0.750
5 T 3 0.600
6 T 3 0.500
7 T 3 0.429
8 T 3 0.375
9 T 3 0.333
10 H 4 0.400
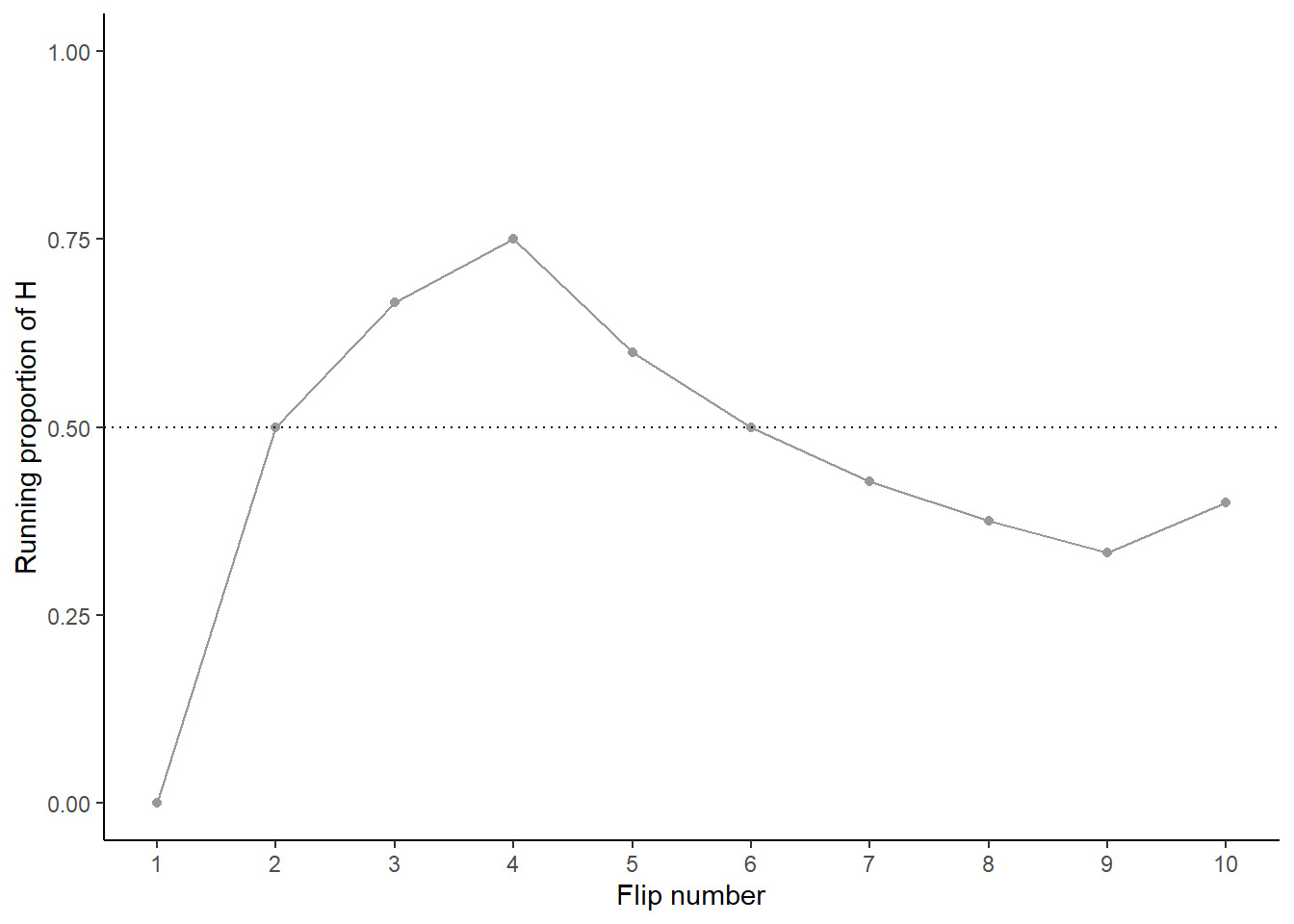
Running proportion of H versus number of flips for the 10 coin flips in Table 1.2.

Figure 1.3: Running proportion of H versus number of flips for the 10 coin flips in Table 1.2.

Now we’ll flip the coin 90 more times for a total of 100 flips. The plot on the left in Figure 1.4 summarizes the results, while the plot on the right also displays the results for 3 additional sets of 100 flips. The running proportion fluctuates considerably in the early stages, but settles down and tends to get closer to 0.5 as the number of flips increases. However, each of the fours sets results in a different proportion of heads after 100 flips: 0.41 (gray), 0.49 (orange), 0.52 (blue), 0.53 (green). Even after 100 flips the proportion of flips that result in H isn’t guaranteed to be very close to 0.5.

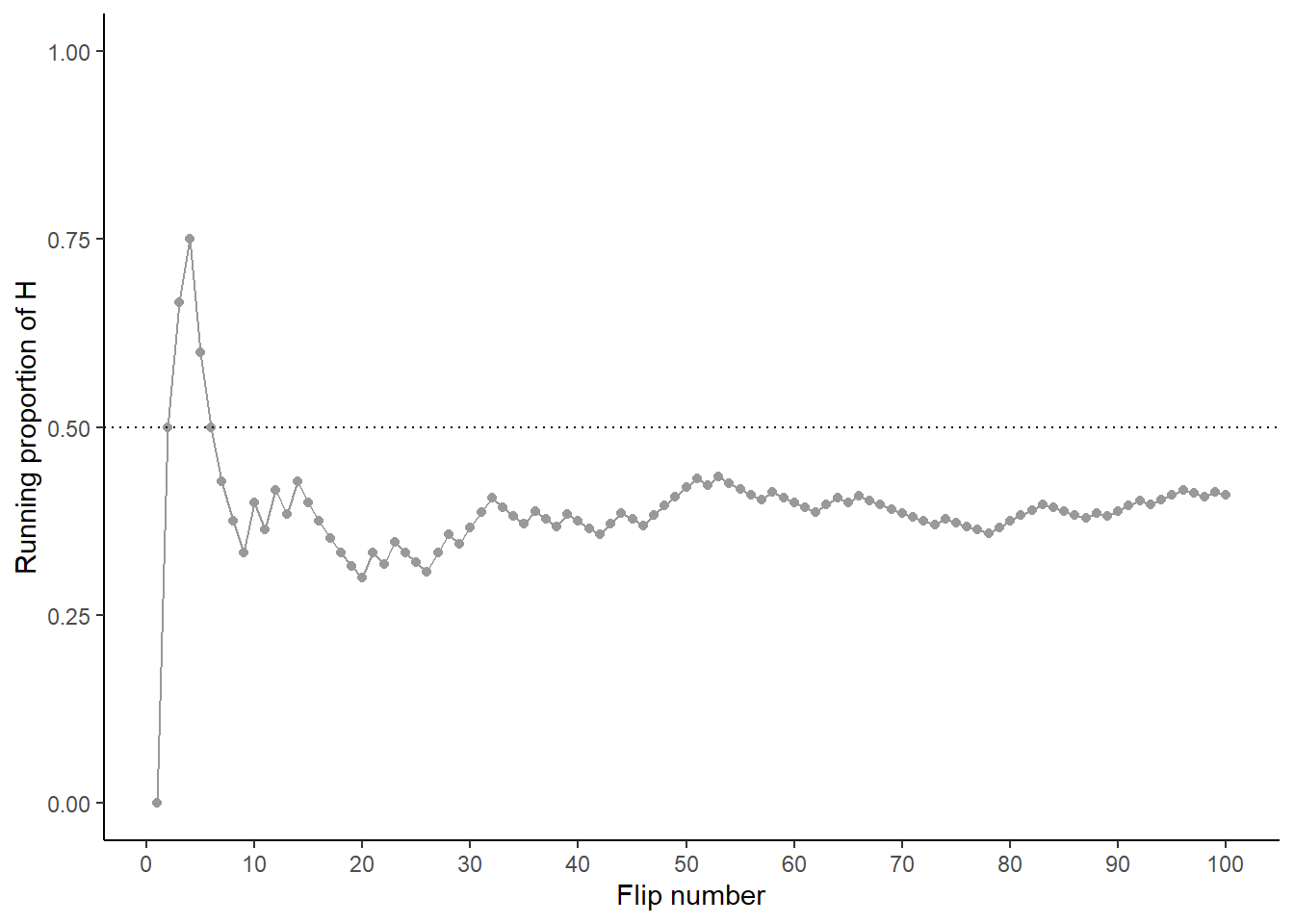
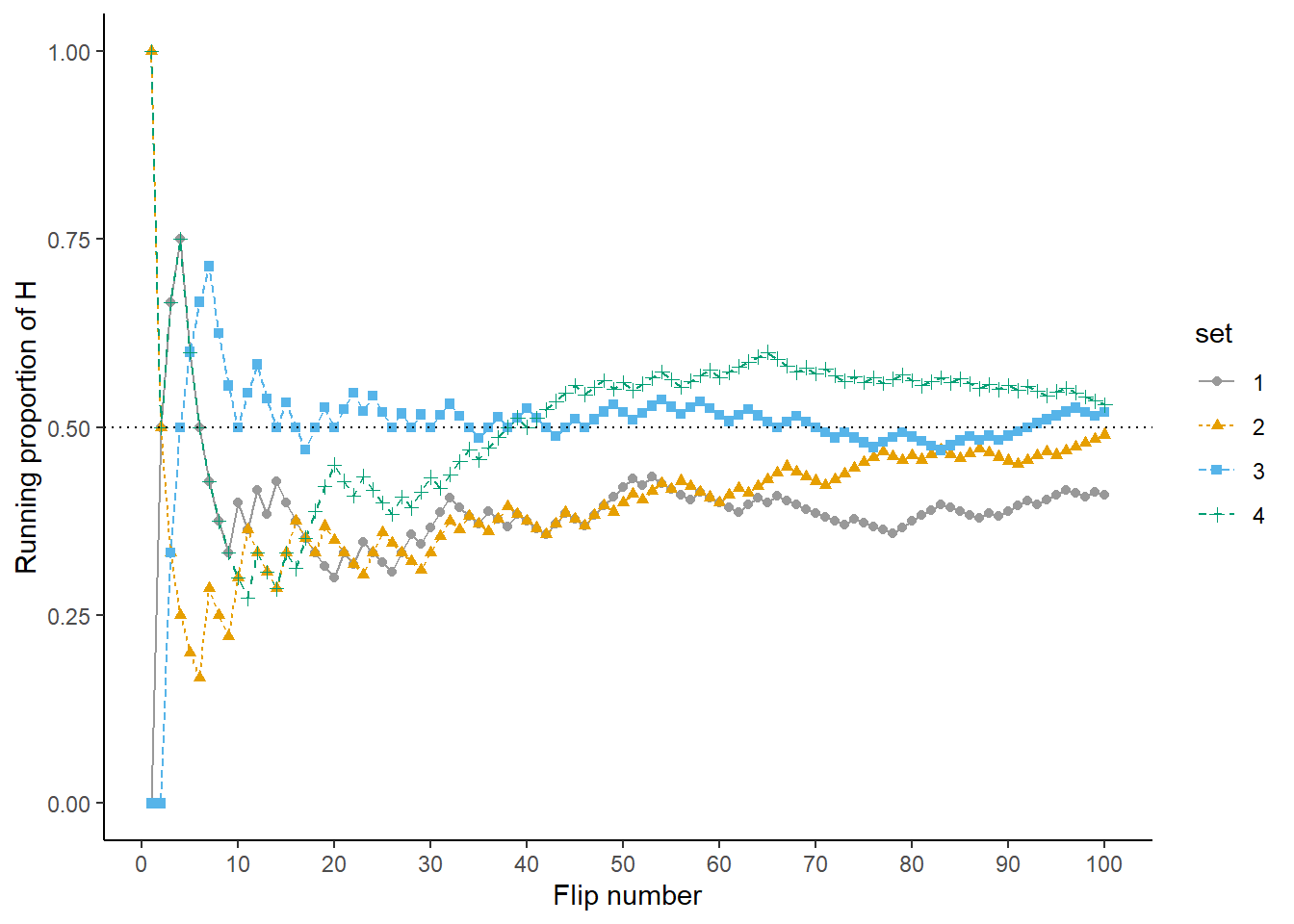
Running proportion of H versus number of flips for four sets of 100 coin flips.Running proportion of H versus number of flips for four sets of 100 coin flips.

Figure 1.4: Running proportion of H versus number of flips for four sets of 100 coin flips.

Now for each set of 100 flips, we’ll flip the coin 900 more times for a total of 1000 flips in each of the four sets. The plot on the left in Figure 1.5 summarizes the results for our original set, while the plot on the right also displays the results for the three additional sets. Again, the running proportion fluctuates considerably in the early stages, but settles down and tends to get closer to 0.5 as the number of flips increases. Compared to the results after 100 flips, there is less variability between sets in the proportion of H after 1000 flips: 0.498 (gray), 0.485 (orange), 0.506 (blue), 0.462 (green). Now, even after 1000 flips the proportion of flips that result in H isn’t guaranteed to be exactly 0.5, but we see a tendency for the proportion to get closer to 0.5 as the number of flips increases.

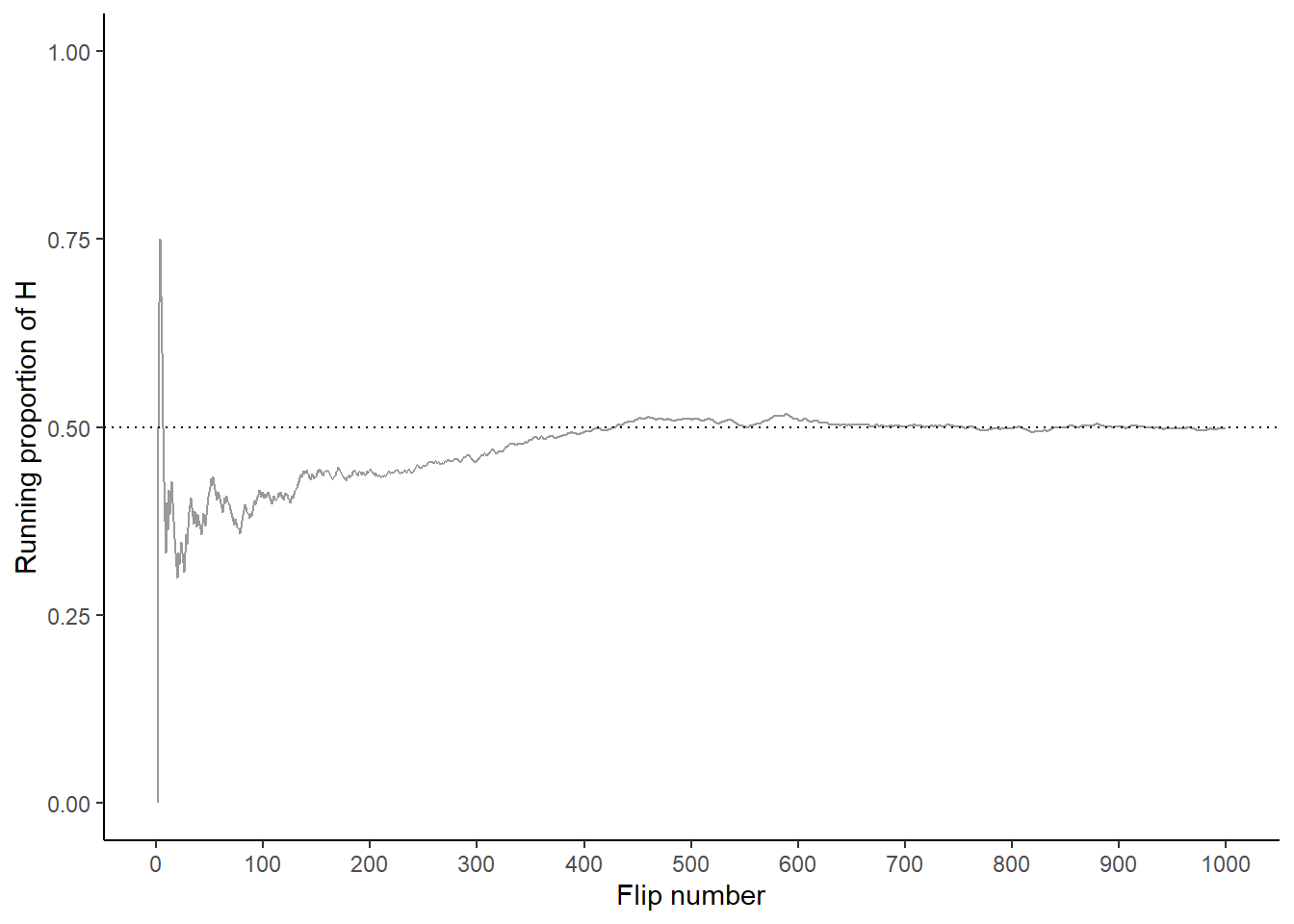
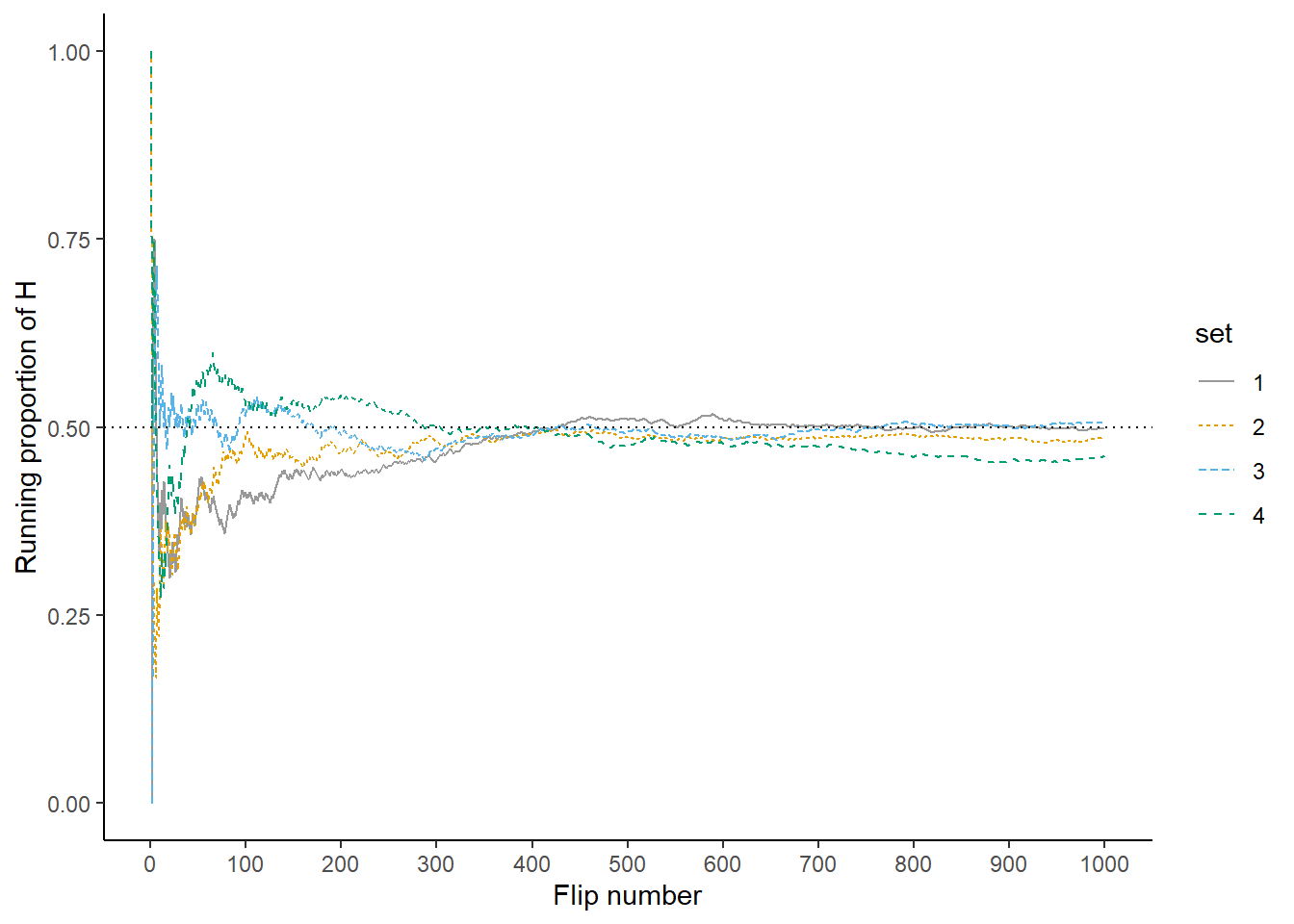
Running proportion of H versus number of flips for four sets of 1000 coin flips.Running proportion of H versus number of flips for four sets of 1000 coin flips.

Figure 1.5: Running proportion of H versus number of flips for four sets of 1000 coin flips.

In summary, in a large number of flips of a fair coin we expect about 50% of flips to result in H. That is, the probability that a flip of a fair coin results in H can be interpreted as the long run proportion of flips that result in H, or in other words, the long run relative frequency of H.

In general, the probability of an event associated with a random phenomenon can be interpreted as a long run proportion or long run relative frequency: the probability of the event is the proportion of times that the event would occur in a very large number of hypothetical repetitions of the random phenomenon. A natural question is: “how many repetitions are required to represent the long run?” We’ll return to this question and the idea of long run relative frequency in later chapters.

The long run relative frequency interpretation of probability can be applied when a situation can be repeated numerous times, at least conceptually, and an outcome can be observed for each repetition. One benefit of the relative frequency interpretation is that the probability of an event can be approximated by simulating the random phenomenon a large number of times and determining the proportion of simulated repetitions on which the event occurred out of the total number of repetitions in the simulation. A simulation involves an artificial recreation of the random phenomenon, usually using a computer. After many repetitions the relative frequency of the event will settle down to a single constant value, and that value is the approximately the probability of the event.

Of course, the accuracy of simulation-based approximations of probabilities depends on how well the simulation represents the actual random phenomenon. Conducting a simulation can involve many assumptions which influence the results. Simulating many flips of a fair coin is one thing; simulating an entire NFL season and the winner of the Superbowl is an entirely different story.

Example 1.2 In each of the following, write a clearly worded sentence interpreting the numerical value of the probability as a long run relative frequency in context. (Just take the numerical values— 0.1, 0.25, and 0.73 — as given. We’ll see how to compute probabilities like these later.)

  1. The probability that a roll of a fair ten-sided die lands on 1 is 0.1.
  2. The probability that two flips of a fair coin both land on H is 0.25.
  3. The probability that in 100 flips of a fair coin the proportion of flips that land on H is between 0.45 and 0.55 is 0.73.

Solution. to Example 1.2

Show/hide solution
  1. About 10% of rolls of a fair ten-sided result in a roll of 1. The phenomenon is a roll of a far ten-sided die and the event of interest is whether the die lands on 1. If we rolled a fair ten-sided die many, many times, we would expect the proportion of rolls that landed on 1 to be close to 0.1.
  2. In about 25% of sets of two fair coin flips, both flips in the set land on H. The phenomenon involves two flips of a coin, so we consider what would happen over many sets of two flips each.
  3. In about 73% of sets of 100 fair coin flips, the proportion of H for the set is between 0.45 and 0.55. The phenomenon involves 100 coin flips, so we consider many sets of 100 coin flips each, each set resulting in a proportion of H that is either between 0.45 and 0.55 or not. Imagine adding many more paths to the plot on the right in Figure Figure 1.4, each corresponding to a set of 100 flips, and seeing how many of the paths result in a value between 0.45 and 0.55 at flip 100.

1.2.2 Subjective probability

The long run relative frequency interpretation is natural in repeatable situations like flipping coins, rolling dice, drawing Powerballs, or randomly selecting Cal Poly students.

On the other hand, it is difficult to conceptualize some scenarios in the long run. Superbowl 2023 will only be played once, the 2024 U.S. Presidential Election will only be conducted once (we hope), and there was only one April 17, 2009 on which you either did or did not eat an apple. But while these situations are not naturally repeatable they still involve randomness (uncertainty) and it is still reasonable to assign probabilities. At this point in time we might think that the Kansas City Chiefs are more likely than the Jacksonville Jaguars to win Superbowl 2023 and that President Biden is more likely than Dwayne Johnson to win the U.S. 2024 Presidential Election. If you’ve always been an apple-a-day person, you might think there’s a good chance you ate one on April 17, 2009. It is still reasonable to assign probabilities to quantify such assessments even when an uncertain phenomenon is not repeated.

However, the meaning of probability does seem different in a physically repeatable situations like coin flips than in single occurrences like the 2023 Superbowl. Let’s switch sports and consider the 2022 World Series of Major League Baseball. As of June 17, 2022,

  • According to FiveThirtyEight, the Los Angeles Dodgers have a 20% chance of winning the 2022 World Series, and the San Diego Padres have an 8% chance.
  • According to FanGraphs, the Dodgers have a 12.4% chance of winning the 2022 World Series, and the Padres have a 9.9% chance.
  • According to gambling site Odds Shark, the Dodgers have a 20% chance of winning the 2022 World Series, and the Padres have a 7.7% chance.

Each source, as well as many others, assigns different probabilities to the Dodgers or Padres winning. Which source, if any, is “correct”?

When the situation involves a fair coin flip, we could perform a simulation to see that the long run proportion of flips that land on H is 0.5, and so the probability that a fair coin flip lands on H is 0.5. Even though the actual 2022 World Series will only happen once, we could still perform a simulation involving hypothetical repetitions. However, simulating the World Series involves first simulating the 2022 season to determine the playoff matchups, then simulating the playoffs to see which teams make the World Series, then simulating the World Series matchup itself. And simulating the 2022 season involves simulating all the individual games. Even just simulating a single game involves many assumptions; differences in opinions with regards to these assumptions can lead to different probabilities. For example, on June 17, according to FiveThirtyEight the Dodgers had a 68% chance of beating the Cleveland Guardians in their game on June 17, but according to FanGraphs it was 66%. Even if the differences in probabilities between sources is small, many small differences over the course of the season could result in large differences in predictions for the World Series champion.

Unlike physically repeatable situations such as flipping a coin, there is no single set of “rules” for conducting a simulation of a season of baseball games or the World Series champion. Therefore, there is no single long run relative frequency that determines the probability. Instead we consider subjective probability.

A subjective (a.k.a. personal) probability describes the degree of likelihood a given individual assigns to a certain event. As the name suggests, different individuals (or probabilistic models) might have different subjective probabilities for the same event. In contrast, in the long run relative frequency interpretation the probability is agreed to be defined as the long run relative frequency, a single number.

Think of subjective probabilities as measuring relative degrees of likelihood, uncertainty, or plausibility rather than long run relative frequencies. For example, in the FiveThirtyEight forecast, the Dodgers are about 2.5 times more likely to win the World 2022 Series than the Padres (\(2.5 = 20 / 8\)). Relative likelihoods can also be compared across different forecasts or scenarios. For example, FiveThirtyEight believes that the Dodgers are about 1.6 times more likely to win the World Series than FanGraphs does. Also, FiveThirtyEight believes that the likelihood that a fair coin lands on H is about 2.5 times larger than the likelihood that the Dodgers win the 2022 World Series.

The FiveThirtyEight MLB predictions are the output of a probabilistic forecast. A probabilistic forecast combines observed data and statistical models to make predictions. Rather than providing a single prediction (such as “the Los Angeles Dodgers will win the 2022 World Series”), probabilistic forecasts provide a range of scenarios and their relative likelihoods. Such forecasts are subjective in nature, relying upon the data used and assumptions of the model. Changing the data or assumptions can result in different forecasts and probabilities. In particular, probabilistic forecasts are usually revised over time as more data becomes available.

Simulations can also be based on subjective probabilities. If we were to conduct a simulation consistent with FiveThirtyEight’s model (as of June 17), then in about 20.9% of repetitions the Dodgers would win the World Series, and in about 8% of repetitions the Padres would win. Of course, different sets of subjective probabilities correspond to different assumptions and different ways of conducting the simulation.

Subjective probabilities can be calibrated by weighing the relative favorability of different bets, as in the following example.

Example 1.3 What is your subjective probability that Professor Ross has a TikTok account? Consider the following two bets, and suppse you must choose only one5.

  1. You win $100 if Professor Ross has a TikTok account, and you win nothing otherwise.
  2. A box contains 40 green and 60 gold marbles that are otherwise identical. The marbles are thoroughly mixed and one marble is selected at random. You win $100 if the selected marble is green, and you win nothing otherwise.
  1. Which of the above bets would you prefer? Or are you completely indifferent? What does this say about your subjective probability that Professor Ross has a Tik Tok account?
  2. If you preferred bet B to bet A, consider bet C which has a similar setup to B but now there are 20 green and 80 gold marbles. Do you prefer bet A or bet C? What does this say about your subjective probability that Professor Ross has a Tik Tok account?
  3. If you preferred bet A to bet B, consider bet D which has a similar setup to B but now there are 60 green and 40 gold marbles. Do you prefer bet A or bet D? What does this say about your subjective probability that Professor Ross has a Tik Tok account?
  4. Continue to consider different numbers of green and gold marbles. Can you zero in on your subjective probability?

Solution. to Example 1.3

Show/hide solution
  1. Since the two bets have the same payouts, you should prefer the one that gives you a greater chance of winning! If you choose bet B you have a 40% chance of winning.
    • If you prefer bet B to bet A, then your subjective probability that Professor Ross has a TikTok account is less than 40%.
    • If you prefer bet A to bet B, then your subjective probability that Professor Ross has a TikTok account is greater than 40%.
    • If you’re indifferent between bets A and B, then your subjective probability that Professor Ross has a TikTok account is equal to 40%.
  2. If you choose bet C you have a 20% chance of winning.
    • If you prefer bet C to bet A, then your subjective probability that Professor Ross has a TikTok account is less than 20%.
    • If you prefer bet A to bet C, then your subjective probability that Professor Ross has a TikTok account is greater than 20%.
    • If you’re indifferent between bets A and C, then your subjective probability that Professor Ross has a TikTok account is equal to 20%.
  3. If you choose bet D you have a 60% chance of winning.
    • If you prefer bet D to bet A, then your subjective probability that Professor Ross has a TikTok account is less than 60%.
    • If you prefer bet A to bet D, then your subjective probability that Professor Ross has a TikTok account is greater than 60%.
    • If you’re indifferent between bets A and D, then your subjective probability that Professor Ross has a TikTok account is equal to 60%.
  4. Continuing in this way you can narrow down your subjective probability. For example, if you prefer bet B to bet A and bet A to bet C, your subjective probability is between 20% and 40%. Then you might consider bet E corresponding to 30 gold marbles and 70 green to determine if you subjective probability is greater than or less than 30%. At some point it will be hard to choose, and you will be in the ballpark of your subjective probability. (Think of it like going to the eye doctor: “which is better: 1 or 2?” At some point you can’t really see a difference.)
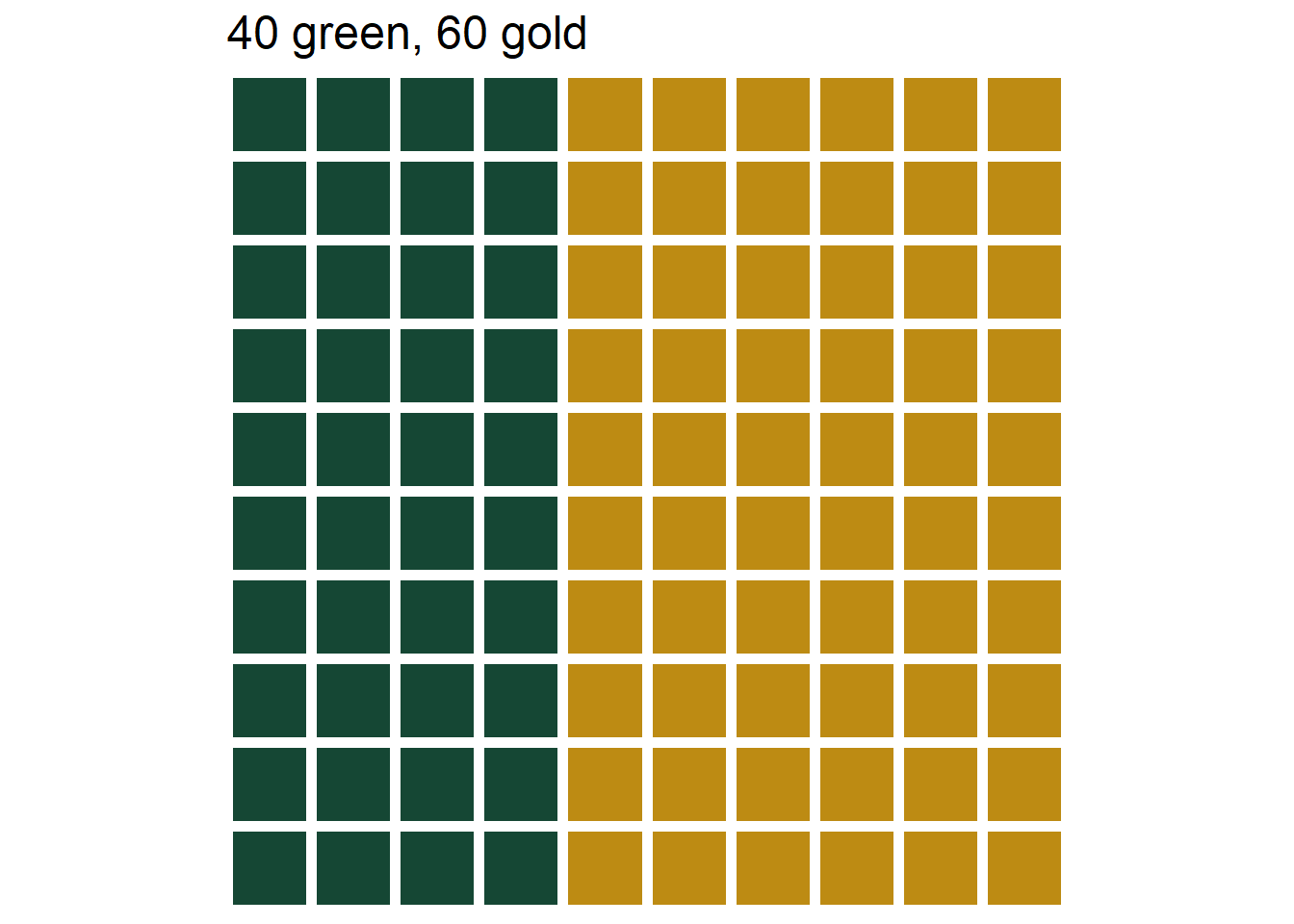
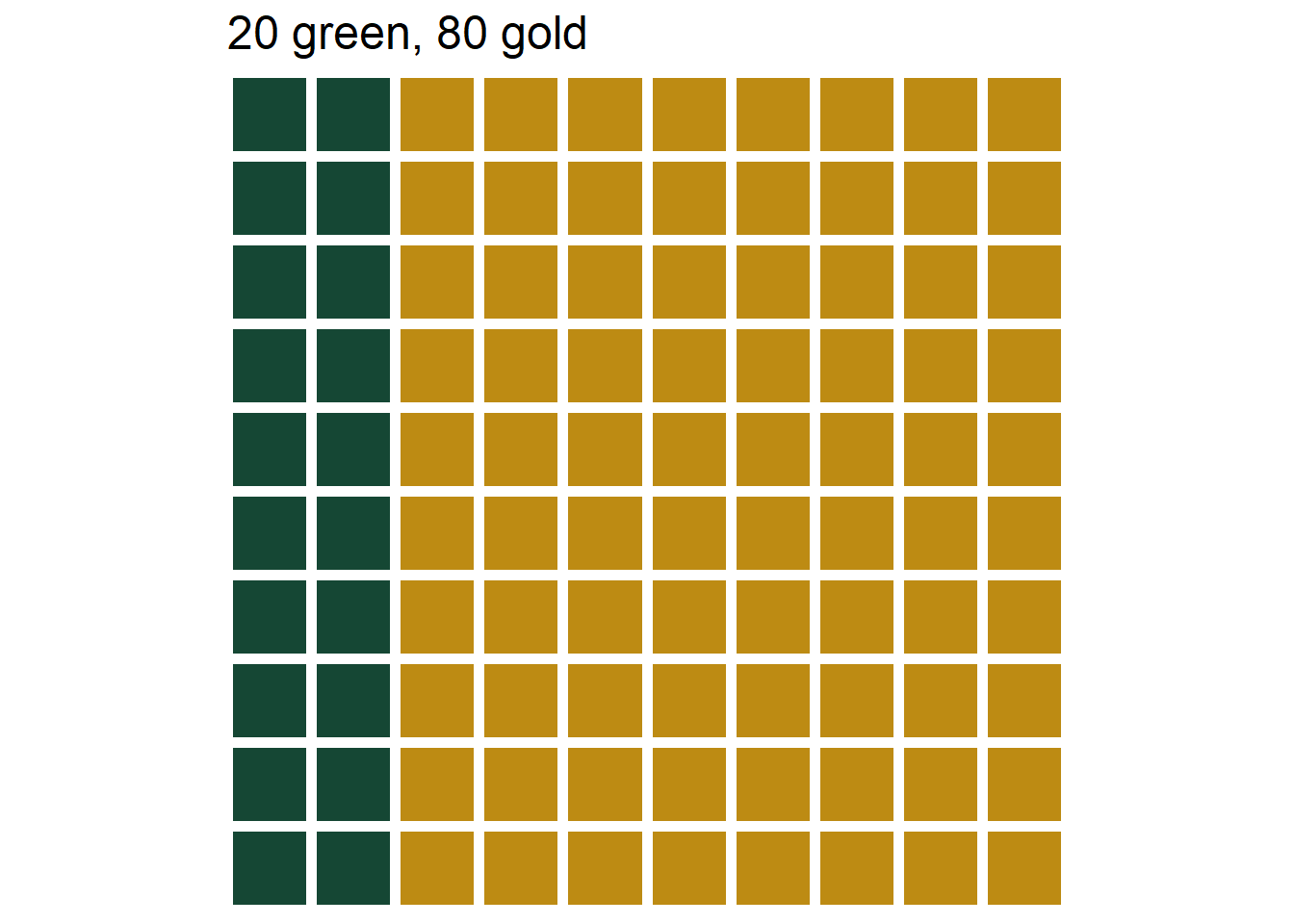
The three marble bins in Example 1.3. Left: Bet A, 40% chance of selecting green. Middle: Bet B, 20% chance of selecting green. Left: Bet C, 60% chance of selecting green.The three marble bins in Example 1.3. Left: Bet A, 40% chance of selecting green. Middle: Bet B, 20% chance of selecting green. Left: Bet C, 60% chance of selecting green.The three marble bins in Example 1.3. Left: Bet A, 40% chance of selecting green. Middle: Bet B, 20% chance of selecting green. Left: Bet C, 60% chance of selecting green.

Figure 1.6: The three marble bins in Example 1.3. Left: Bet A, 40% chance of selecting green. Middle: Bet B, 20% chance of selecting green. Left: Bet C, 60% chance of selecting green.

Of course, the strategy in the above example isn’t an exact science, and there is a lot of behavioral psychology behind how people make choices in situations like this, especially when betting with real money. But the example provides a very rough idea of how you might discern a subjective probability of an event. The example also illustrates that probabilities can be “personal”; your information or assumptions will influence your assessment of the likelihood.

We close this section with some brief comments about subjectivity. Subjectivity is not bad; “subjective” is not a “dirty” word. Any probability model involves some subjectivity, even when probabilities can be interpreted naturally as long run relative frequencies. For example, assuming a die is fair does not codify an objective truth about the die. Instead, “fairness” reflects a reasonable and tractable mathematical model. In the real world, any “fair” six-sided die has small physical imperfections that cause the six faces to have different probabilities. However, the differences are usually small enough to be ignored for most practical purposes. Assuming that the probability that the die lands on each side is 1/6 is much more tractable than assuming the probability of a 1 is 0.1666666668, the probability of a 2 is 0.1666666665, etc. (Furthermore, measuring the probability of each side so precisely would be extremely difficult.) But assuming that the probability that the die lands on each side is 1/6 is also subjective. We might agree more easily on the probability that a six-sided die lands on 1 than on the probability that the Dodgers win the 2021 World Series. But the fact that there cam be many reasonable probability models for a situation like the 2021 World Series does not make the corresponding subjective probabilities any less valid than long run relative frequencies.

1.2.3 Exercises

  1. In each of the following, write a clearly worded sentence interpreting the numerical value of the probability as a long run relative frequency in context. (Just take the numerical values as given for now. We’ll see how to compute probabilities like these later.)

    1. The probability of rolling doubles when you roll two fair six-sided dice is 1/6.
    2. The probability of rolling doubles on three consecutive rolls of two fair six-sided dice is 0.00463.
    3. The probability that the sum of 100 rolls of a fair six-sided die is less than 370 is 12%.
    4. Roll a fair six-sided die until you roll a 6 three times and then stop. The probability that you roll the die at least 10 times is 0.822.

  2. Various sources post odds for who will win the 2024 U.S. Presidential Election. As of July 28, 2021, the website bonus.com lists the following probabilities.

    Potential candidate Probability of winning 2024 election
    Joe Biden 20.0%
    Kamala Harris 16.7%
    Donald Trump 12.5%
    Nikki Haley 7.7%
    Ron DeSantis 7.7%
    1. According to bonus.com, how many times more likely is Joe Biden to win than Nikki Haley is to win?
    2. According to bonus.com, is the probability that Nikki Haley wins the Republican nomination greater than, less than, or equal to 7.7%? Why?
    3. Another source list the probability for Kamala Harris as 22%. How many times more likely is Kamala Harris to win according to this source relative to bonus.com?
    4. Say it’s October 2024. How do you think the above table would change? We obviously can’t predict the future, but in general terms what would you expect a table like this to look like a month before the election?

  3. Identify your subjective probability of each of the following (to the nearest 5% or 10% is fine). Explain how you arrived at your value by considering bets like those in Example 1.3.

    1. The probability that a Cal Poly team will ever win an NCAA Division I championship.
    2. The probability that you will eventually visit all 50 U.S. states at some time in your life.
    3. The probability that we live in a multiverse.
    4. Choose a situation of interest to you and identify your subjective probability!

  1. The Grand Duke of Tuscany posed this problem to Galileo, who published his solution in 1620. However, unbeknownst to Galileo, the same problem had been solved almost 100 years earlier by Gerolamo Cardano, one of the first mathematicians to study probability.↩︎

  2. We do not advocate gambling. We merely use gambling contexts to motivate probability concepts.↩︎