1.6 Appendix: Properties of Exponentials and Logarithms

The computation of continuously compounded returns requires the use of natural logarithms. The natural logarithm function, $\ln(\cdot),$ is the inverse of the exponential function, $e^{(\cdot)}=\exp(\cdot),$ where $e^{1}=2.718.$ That is, $\ln(x)$ is defined such that $x=\ln(e^{x}).$ Figure 1.6 plots $e^{x}$ and $\ln(x)$. Notice that $e^{x}$ is always positive and increasing in $x$. $\ln(x)$ is monotonically increasing in $x$ and is only defined for $x>0.$ Also note that $\ln(1)=0$ and $\ln(0)=-\infty.$

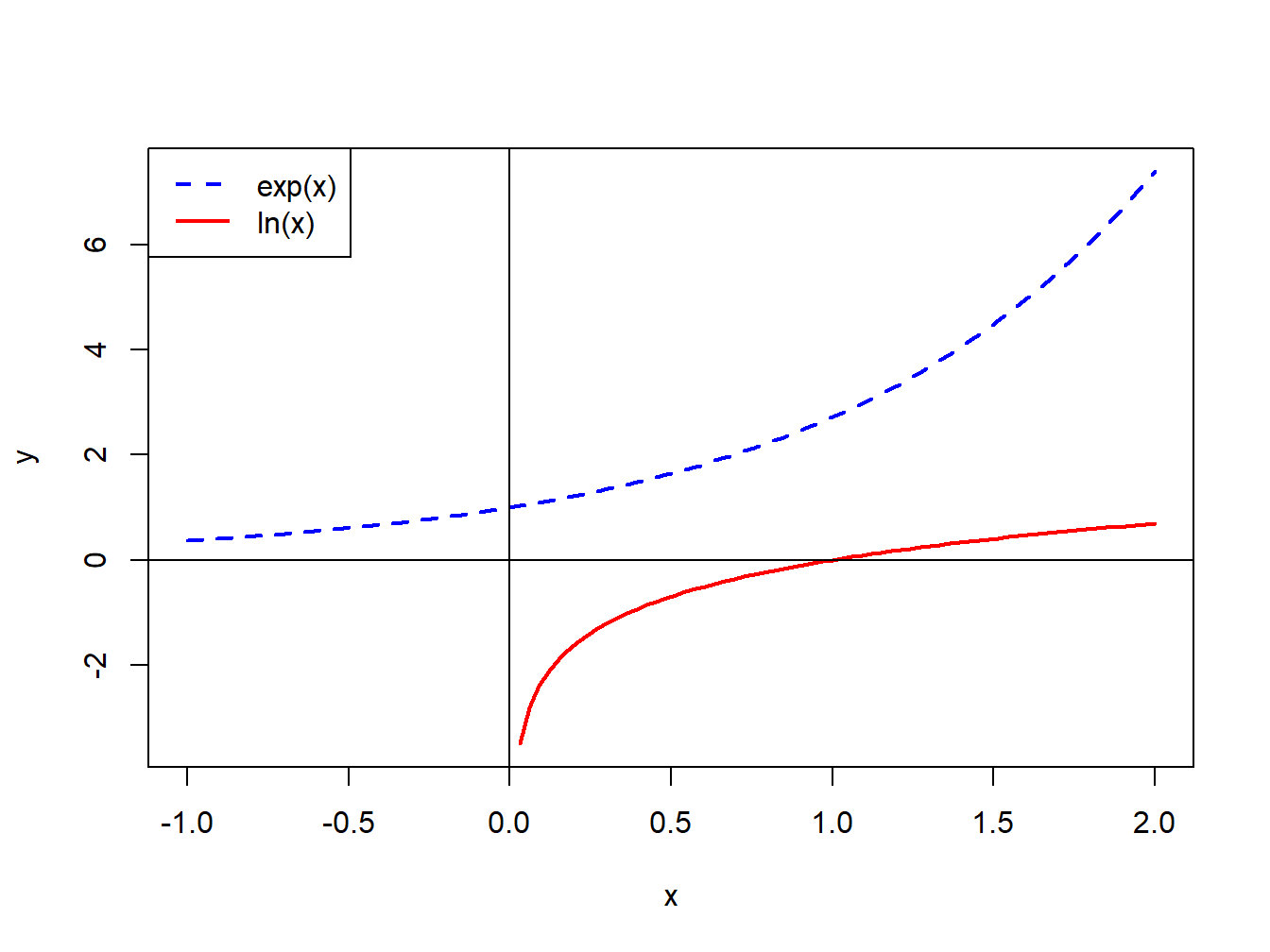
Figure 1.6: Exponential and natural logarithm functions.

The exponential and natural logarithm functions have the following properties:

1. $\ln(x\cdot y)=\ln(x)+\ln(y),$ $x,y>0$
2. $\ln(x/y)=\ln(x)-\ln(y),$ $x,y>0$
3. $\ln(x^{y})=y\ln(x),$ $x>0$
4. $\frac{d\ln(x)}{dx}=\frac{1}{x},$ $x>0$
5. $\frac{d}{dx}\ln(f(x))=\frac{1}{f(x)}\frac{d}{dx}f(x)$ (chain-rule)
6. $e^{x}e^{y}=e^{x+y}$
7. $e^{x}e^{-y}=e^{x-y}$
8. $(e^{x})^{y}=e^{xy}$
9. $e^{\ln(x)}=x$
10. $\frac{d}{dx}e^{x}=e^{x}$
11. $\frac{d}{dx}e^{f(x)}=e^{f(x)}\frac{d}{dx}f(x)$ (chain-rule)