17.2 Distributions: An example

To begin, consider the heights of all Australian adult males. Clearly, the height of all Australian adult males is unknown: no-one has ever, or could ever realistically, measure the height of all Australian adult males. The Australian Bureau of Statistics (ABS), however, takes samples of Australians to compute estimates of the heights and other measurements.
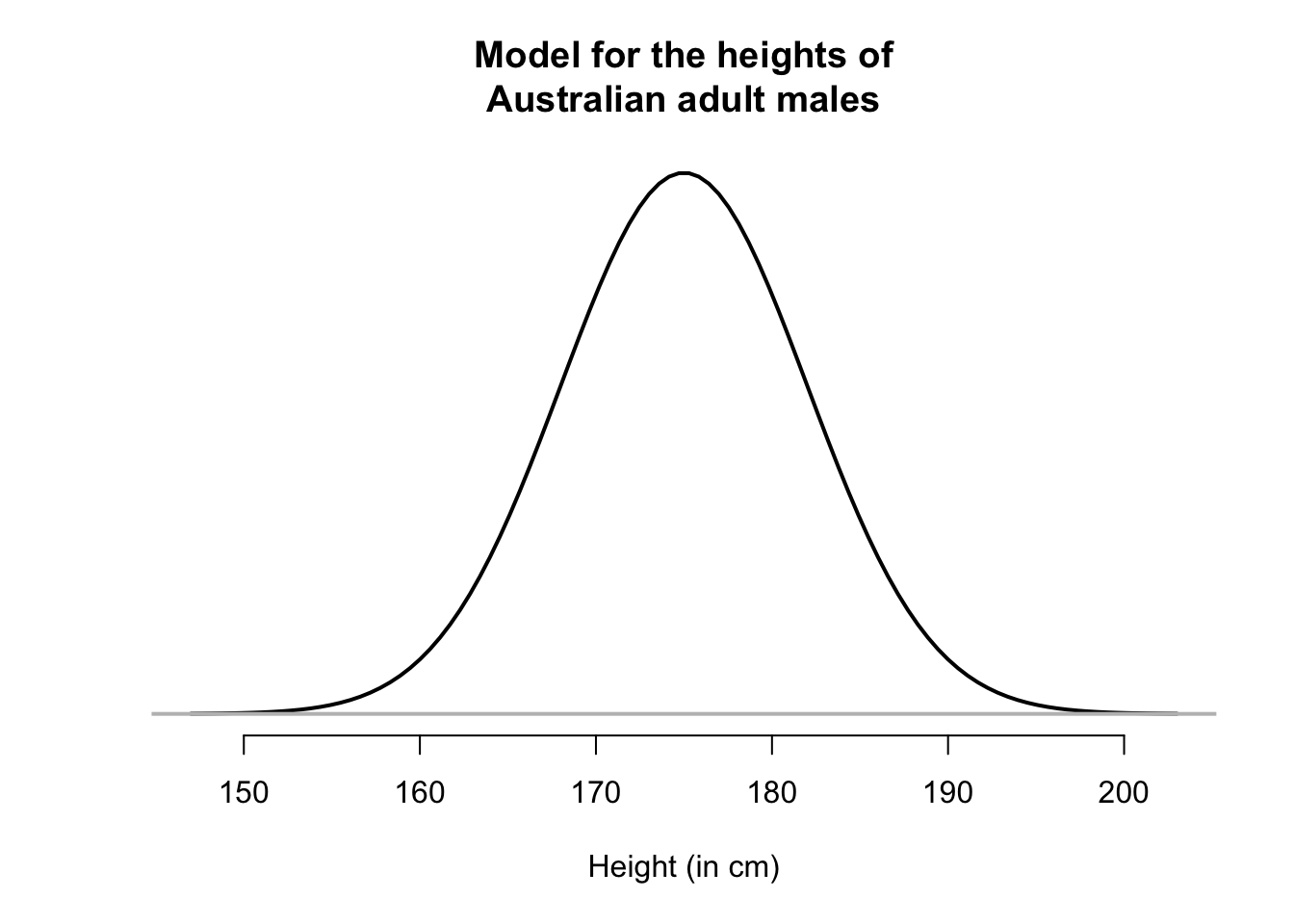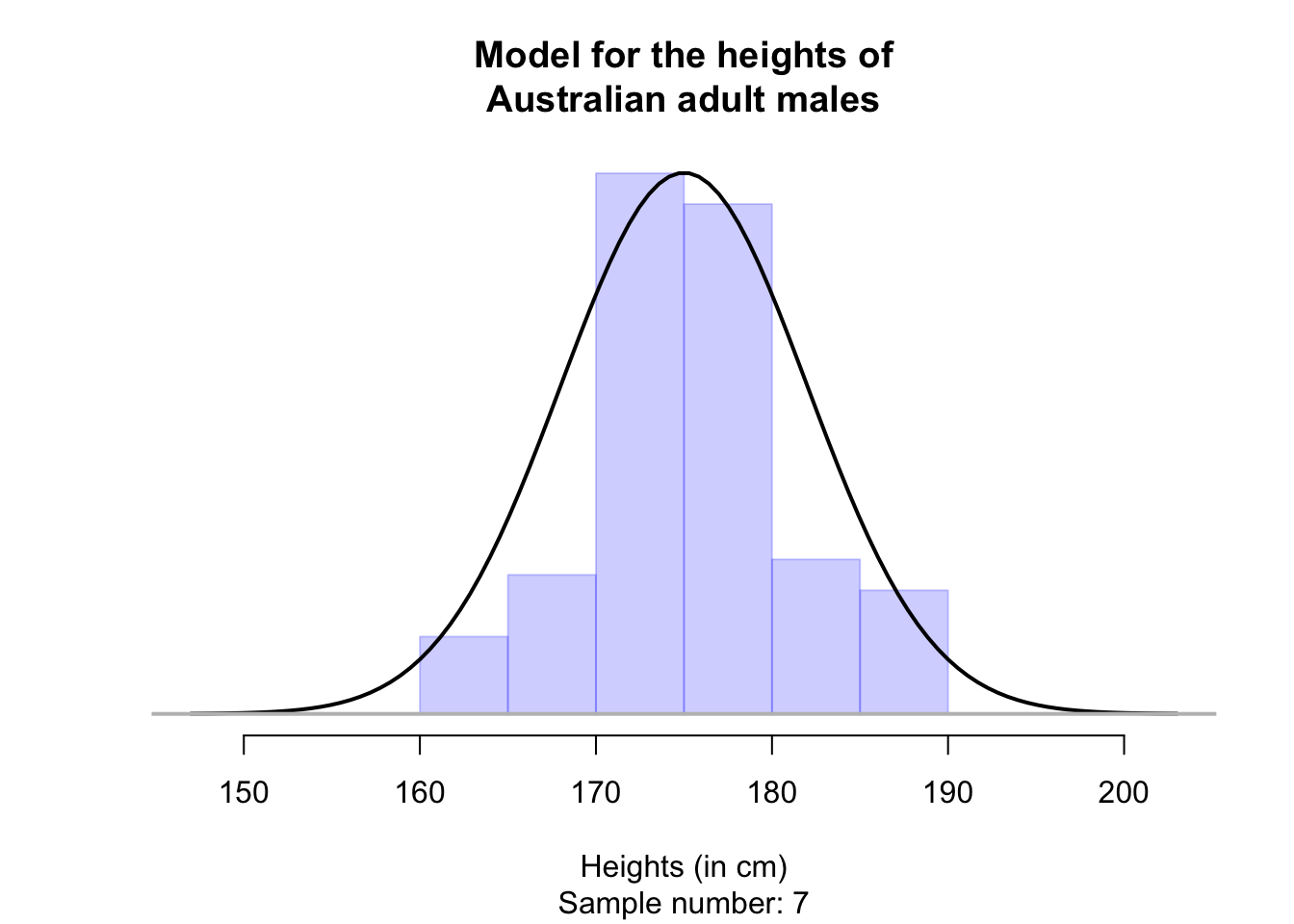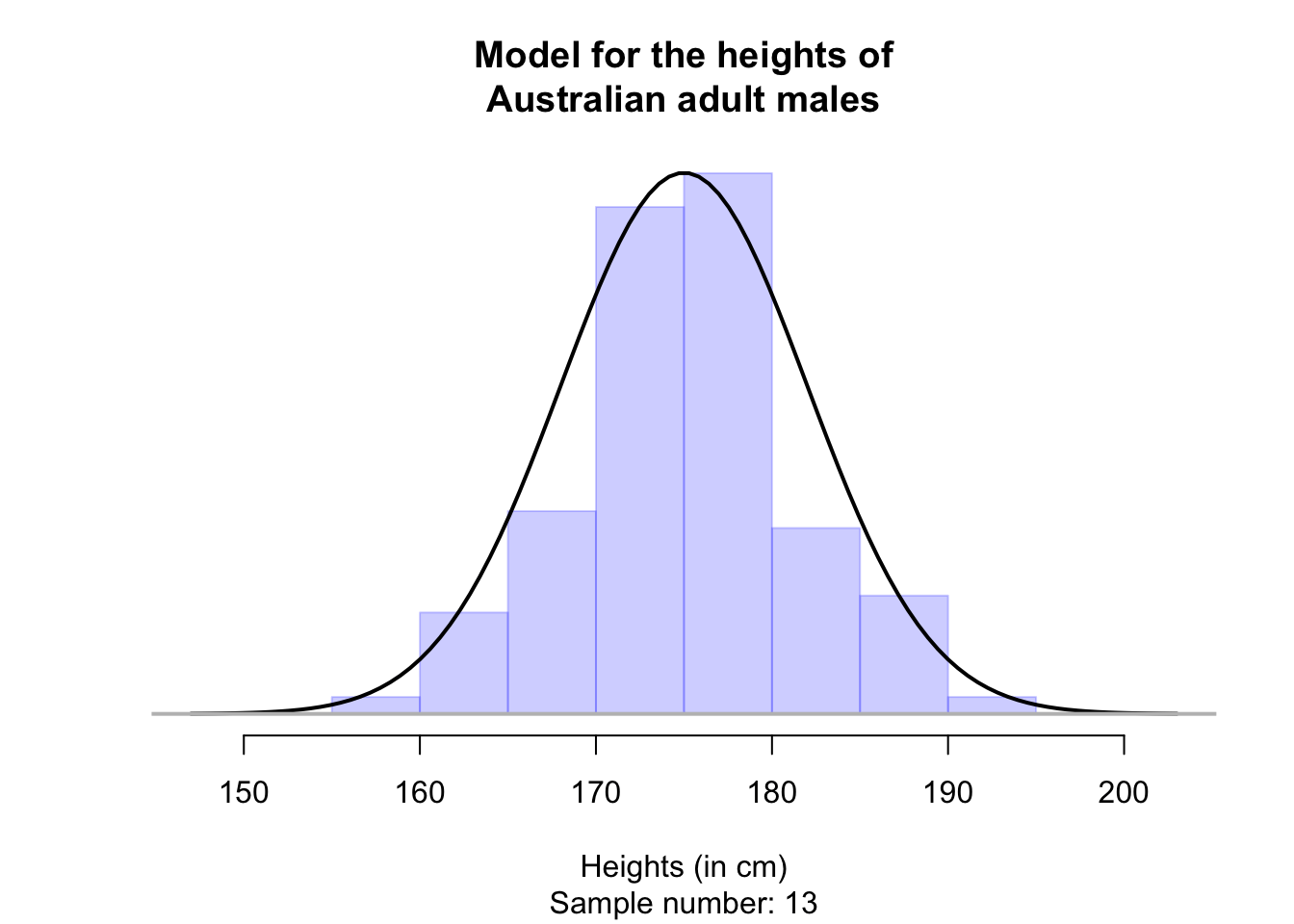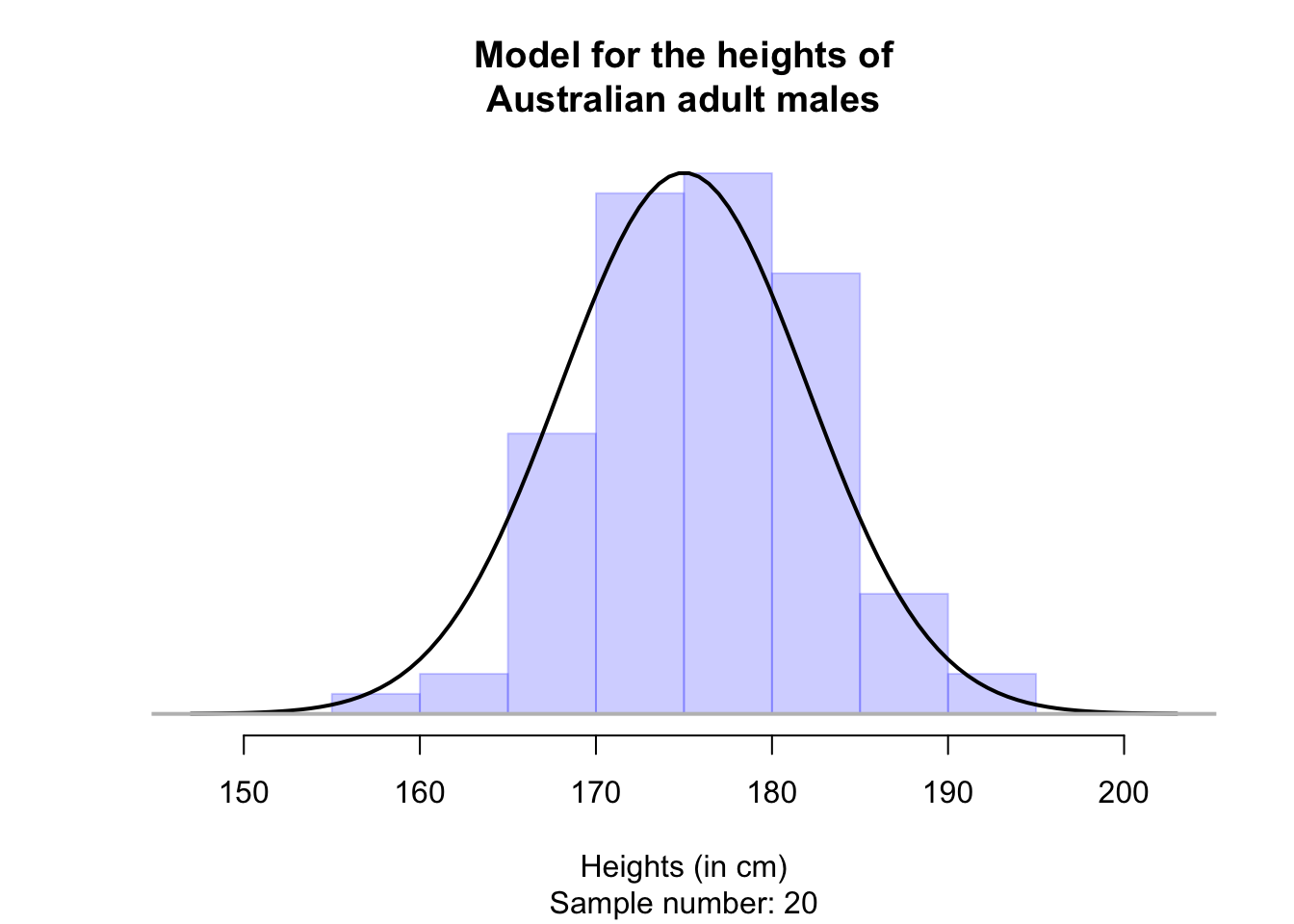
A model could be assumed for the heights of all Australian adult males. This is a theoretical idea that might be a useful description of the heights of Australian adult males in the population. Suppose a model for the heights of Australian adult males is adopted that has:
- a symmetric distribution,
- with a mean height of 175 cm, and
- a standard deviation of 7 cm.
Then, the distribution of the heights of Australian adult males may look like Fig. 17.1. That is, most Australian adult males are between about 168 and 182cm, and very few are taller than 196cm or shorter than 154cm.
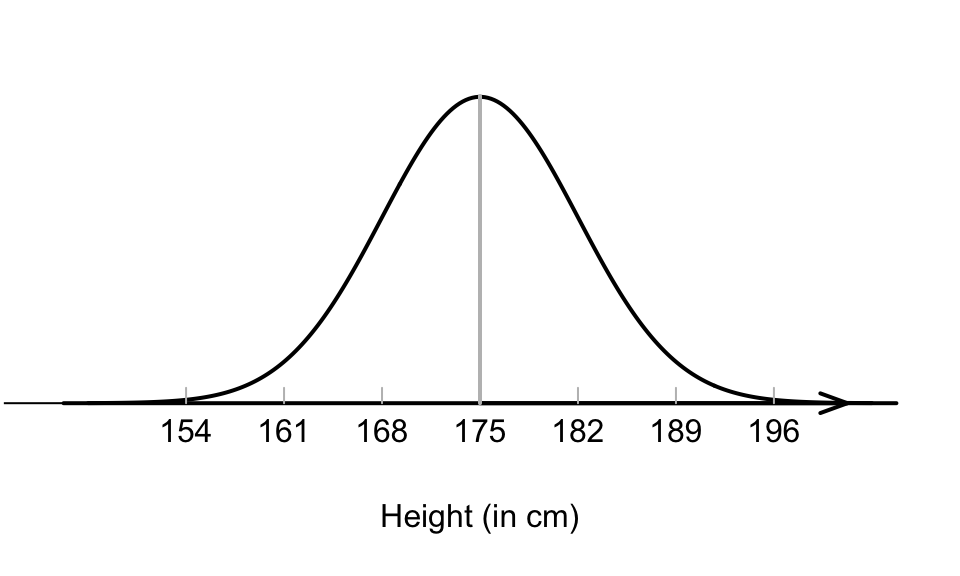
FIGURE 17.1: A model for the heights of Australian adult males
This model represents an idealised, or assumed, picture of the histogram of the heights of all Australian adult males in the population. If this model is a accurate, the distribution of heights in any sample, may be shaped a bit like this, but sampling variation will exist.
Any one sample will look a bit different than this model, but this model captures the general feel of the histogram from many of these samples. For example, see the animation below, where many samples of \(n=100\) men are taken.
The model of heights has approximately a bell-shape: that is, most values are near the average height, but a small number of men are very tall or very short. A bell-shaped distribution is formally called a normal distribution or a normal model. A normal distribution is a way of modelling the population.
A model is a theoretical or ideal concept. In the same way that a model skeleton isn’t 100% accurate (wire joins?) and certainly not exactly like your skeleton, it suitably approximates reality. None of us probably have a skeleton exactly like the model, but the model is still useful and helpful.
Likewise, no variable has exactly a normal distribution, but the model is still useful and helpful. The model is a theoretical way of describing the distribution in the population.