24.13 Exercises

Selected answers are available in Sect. D.23.

Exercise 24.1 Earlier, we studied the NHANES study (Sect. 12.10), and this RQ:

Among Americans, is the mean direct HDL cholesterol different for current smokers and non-smokers?

Use the SPSS output (Fig. 24.16) to answer these questions.

  1. Construct an appropriate table showing the numerical summary.
  2. Determine, and suitably communicate, the 95% CI for the difference between the direct HDL cholesterol values between current smokers and non-smokers.
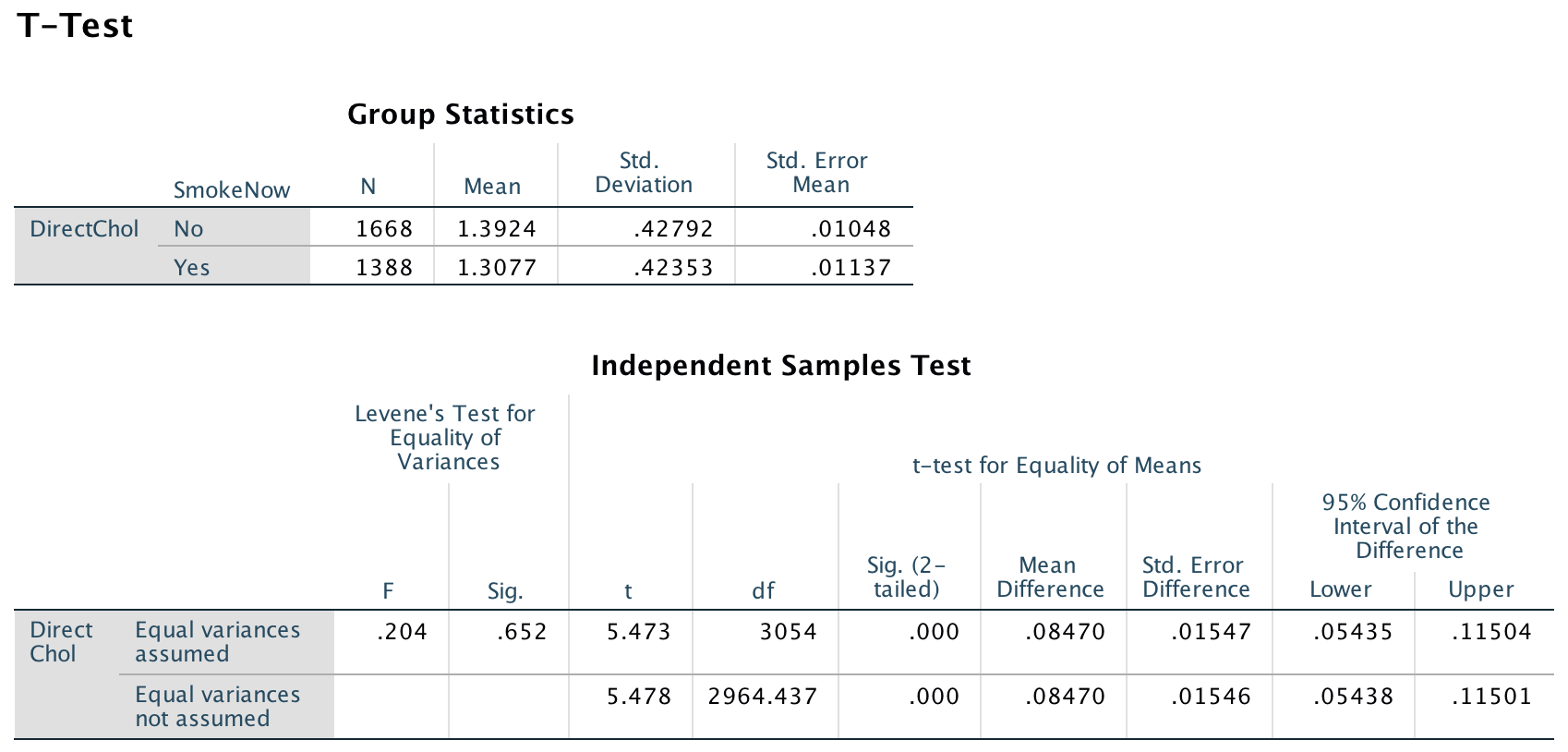
SPSS output for the NHANES data

FIGURE 24.16: SPSS output for the NHANES data

Exercise 24.2 A study (Barrett et al. 2010) of the effectiveness of echinacea to treat the common cold compared, among other things, the duration of the cold for participants treated with echinaca or a placebo. Participants were blinded to the treatment, and allocated to the groups randomly. A summary of the data is given in Table 24.6.

  1. Compute the standard error for the mean duration of symptoms for each group.
  2. Compute an approximate 95% CI for the difference between the mean durations for the two groups.
  3. In which direction is the difference computed? What does it mean when the difference is calculated in this way?
  4. Compute an approximate 95% CI for the population mean duration of symptoms for those treated with echinacea.
  5. Are the CIs likely to be statistically valid?
TABLE 24.6: Numerical summary of duration (in days) of common cold symptoms, for blinded patients taking echinacea or a placebo
Mean Std deviation Std error Sample size
Placebo 6.87 3.62 176
Echinacea 6.34 3.31 183
Difference 0.53 0.367

Exercise 24.3 Carpal tunnel syndrome (CTS) is pain experienced in the wrists. One study (Schmid et al. 2012) compared two different treatments: night splinting, or gliding exercises. Participants were randomly allocated to one of the two groups. Pain intensity (measured using a quantitative visual analog scale; larger values mean greater pain) were recorded after one week of treatment. The data are summarised in Table 24.7.

  1. Compute the standard error for the mean pain intensity for each group.
  2. In which direction is the difference computed? What does it mean when the difference is calculated in this way?
  3. Compute an approximate 95% CI for the difference in the mean pain intensity for the treatments.
  4. Compute an approximate 95% CI for the population mean pain intensity for those treated with splinting.
  5. Are the CIs likely to be statistically valid?
TABLE 24.7: Numerical summary of pain intensity for two different treatments of carpal tunnel syndrome
Mean Std deviation Std error Sample size
Exercise 0.8 1.4 10
Splinting 1.1 1.1 10
Difference 0.3 0.563
Exercise 24.4 A study (Woodward and Walker 1994) examined the sugar consumption in industrialised (mean: 41.8 kg/person/year) and non-industrialised (mean: 24.6 kg/person/year) countries. Using the jamovi output (Fig. 24.17), write down and interpret the CI.
jamovi output for the sugar-consumption data

FIGURE 24.17: jamovi output for the sugar-consumption data

References

Barrett B, Brown R, Rakel D, Mundt M, Bone K, Barlow S, et al. Echinacea for treating the common cold: A randomized trial. Annals of Internal Medicine. 2010;153(12):769–77.
Schmid AB, Elliott JM, Stridwick MW, Little M, Coppeiters MW. Effect of splinting and exercise on intraneural edema of the median nerve in Carpal Tunnel Syndrome—an MRI study to reveal therapeutic mechanisms. Journal of Orthopaedic Research. 2012;30(8):1343–50.
Woodward M, Walker ARP. Sugar consumption and dental caries: Evidence from 90 countries. British Dental Journal. 1994;176:297–302.
Peter K. Dunn, 2021: CC BY-NC-SA 4.0