35.3 Regression using software

In the population, the intercept is denoted by \(\beta_0\) and the slope is denoted by \(\beta_1\). These population values are unknown, and are estimated by the statistics \(b_0\) and \(b_1\) respectively.

The symbol \(\beta\) is the Greek letter ‘beta,’ pronounced ‘beater’ (as in ‘egg beater’).

The formulas for computing \(b_0\) and \(b_1\) are ugly, so we will use software to do the calculations. As usual, the values of these population parameters are unknown, and the values of the sample statistics will change from sample to sample (so they have sampling variation).

For the red deer data again (Fig 33.2), part of the relevant output is shown in Fig. 35.3 (using jamovi) and Fig. 35.4 (using SPSS). From the output, the slope \(b_1\) in the sample is \(b_1 = -0.181\), and the \(y\)-intercept \(b_0\) in the sample is \(b_0 = 4.398\). That is, the values of \(b_0\) and \(b_1\) are in the column labelled Estimate in jamovi, or the column labelled B in SPSS. These are the values of the two regression coefficients; then

\[ \hat{y} = 4.398 + (-0.181\times x), \] which is usually written more simply as

\[ \hat{y} = 4.398 - 0.181 x. \]

The sign of the slope \(b_1\) and the correlation coefficient \(r\) are always the same. For example, if the slope is negative, the correlation coefficient will also be negative.

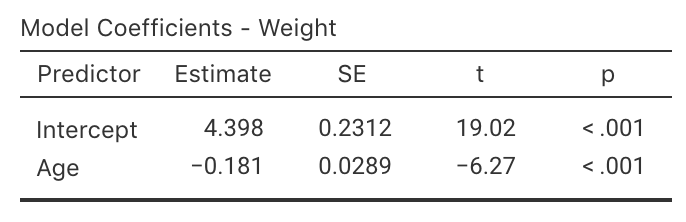
FIGURE 35.3: jamovi output for the red-deer data

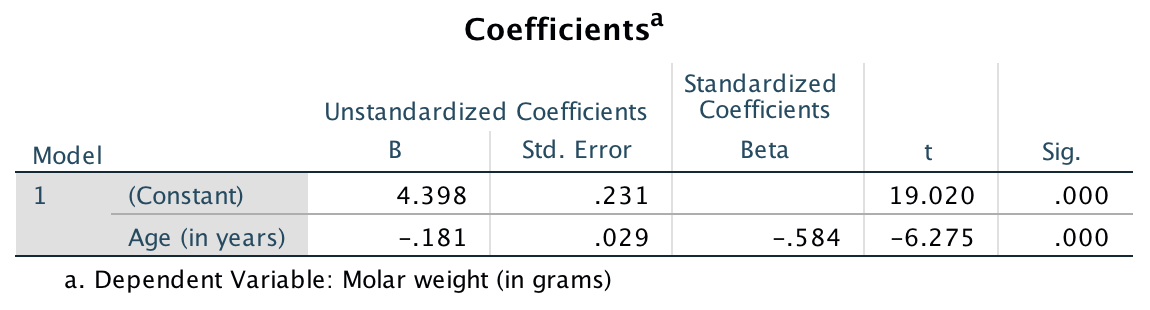
FIGURE 35.4: SPSS output for the red-deer data

Example 35.3 (Regression coefficients) The regression equation for the cyclone data (Fig. 35.2) can be found from the jamovi output (Fig. 35.5): \[ \hat{y} = 12.14 - 2.23x, \] where \(x\) is the ONI (averaged over October, November, December) and \(y\) is the number of cyclones. These values are close the guesses made in Example 35.2.

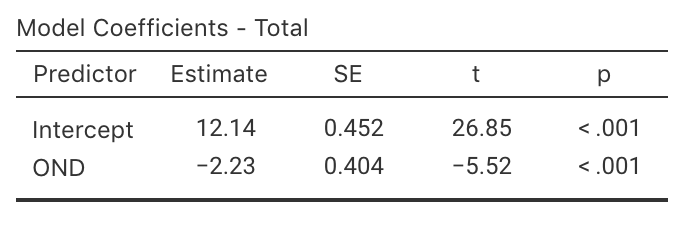
FIGURE 35.5: jamovi output for the cyclone data