25.5 Statistical validity conditions: Comparing odds
As usual, these results hold under certain conditions. The CI computed above is statistically valid if
- All expected counts are at least five.
Some books may give other (but similar) conditions.
In addition to the statistical validity condition, the CI will be
- internally valid if the study was well designed; and
- externally valid if the sample is a simple random sample and is internally valid.
The statistical validity condition is a bit tricky to understand (but is explained further in Sect. 31.3). SPSS will let you know if the expected count condition is not met, underneath the first output table in Fig. 25.3. In jamovi, the expected counts must be explicitly requested to see if this condition is satisfied.
Example 25.2 (Statistical validity) In Fig. 25.3 (for the uni-students data), the text under the first table table of SPSS output (labelled Chi-Square Tests) says
0 cells (0.0%) have expected count less than 5.
That is, all the cells have expected counts of at least five, so the statistical validity condition is satisfied. Notice from Table 25.1 that the observed counts are not all greater than five (one cell has a count of 2). The statistical validity condition is about the expected counts though, not the observed counts.
In jamovi, the expected counts must be requested explicitly (Fig. 25.4), but again none are less than five.
In either case, the conclusion is statistically valid.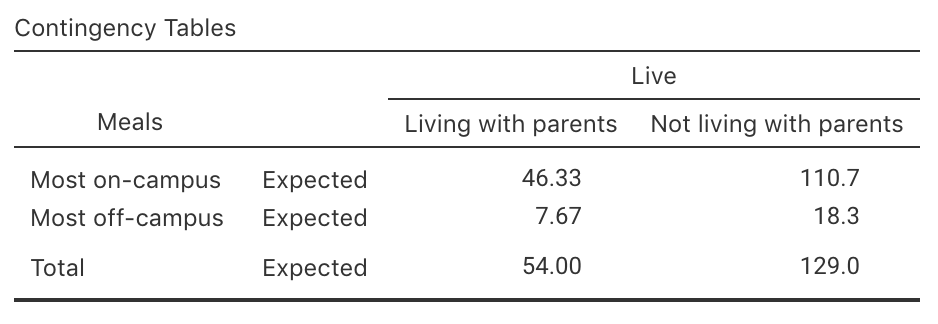
FIGURE 25.4: The expected counts in jamovi, for the uni-students data
Example 25.3 (Car crashes in China) In Example 25.1, all the observed counts are larger than five.
The expected counts are shown below. Since all expected counts are larger than five, the CI will be statistically valid.
| Type of crash | 2011 | 2015 |
|---|---|---|
| Involving pedestrians | 15.11 | 36.88 |
| Involving vehicles | 34.88 | 85.12 |
These counts are what we would expected to find if there was no relationship between the type of crash in 2011 and 2015; that is, if the proportion of crashes involving pedestrians was the same in 2011 and 2015.
The observed counts are very close to these expected counts, meaning that what we observe is very close to what we expected if there was no relatiionship.