2.1 Variable aléatoire stable
Proposition 2.1 Une variable aléatoire \(S\) sera qualifiée de stable si la probabilité est forte qu’une réalisation de cette variable ne s’éloigne pas plus de sa moyenne qu’une limite fixée arbitrairement.
En termes mathématiques, si nous travaillons avec la variable aléatoire \(S\), le principe s’exprime comme:
\[\begin{eqnarray} \Pr[(1-K) \mu_{S} < S < (1+K) \mu_{S}] &\ge& p \label{stab_principle} \end{eqnarray}\]
où :
- \(S\) = Variable aléatoire modélisée (fréquence, sévérité ou charge pure);
- \(\mu_{S} = E[S]\) = Espérance de la variable aléatoire \(S\) (inconnue);
- \(K\) = Variation autorisée autour de \(\mu_{S}\);
- \(p\) = Probabilité que la variation soit plus forte que plus ou moins \(K\).
Proposition 2.2 Si \(S\) respecte la relation précédente pour \(K\) petit (près de 0) et \(p\) grand (près de 1), on dira que la variable aléatoire \(S\) est stable d’ordre (\(K,p\)).
Cela signifie que si nous tirons au hasard une réalisation \(s\) d’une variable aléatoire stable d’ordre (\(K,p\)), il y a une probabilité \(p\) que l’observation \(s\) soit à plus ou moins \(K\)% de la moyenne \(\mu_S\).
2.1.1 Exemple: Loi uniforme
Exemple 2.1 On suppose que \(S \sim Uniforme(100,a)\). Trouvez la condition sur le paramètre \(a\) afin que la variable \(S\) respecte le critère de stabilité d’ordre \((K=0.1, p=0.90)\).
(Exemple à faire en classe)
Le résultat de l’exemple signifie que si nous tirons au hasard un nombre \(s\) d’une loi Uniforme(\(100, 125\)), nous avons 90% des chances que \(s\) soit à plus ou moins 10% de la moyenne \(\mu_S = 112.5\), c’est-à-dire entre \(101.25\) et \(123.75\).
Vérifions le résultat de l’exemple précédent par simulations.
## [1] 122.8702La valeur obtenue est entre \(101.25\) et \(123.75\), mais ce n’est qu’une seule réalisation, qu’un seul tirage.
On pourrait refaire l’exercice plusieurs fois et calculer le nombre de fois qu’un nombre aléatoire tiré de la distribution uniforme(\(a\), \(b\)) respecte la condition de stabilité énoncée plus tôt.
# paramètres de l'uniforme
a <- 100
b <- 125
# moyenne de l'uniforme
mu <- (a+b)/2
# critères de stabilité
K <- 0.10
p <- 0.90
# nb de simulations
n <- 100000
x <- data.frame(runif(n, min = a, max = b))
x %>%
mutate(y = ifelse(x > mu*(1-K) & x < mu*(1+K), 1, 0)) %>%
summarize(percent = 100*sum(y)/n)## percent
## 1 89.882Par curiosité, on peut aussi changer les paramètres de l’uniforme pour voir à quel point le critère de stabilité est touché.
# paramètres de l'uniforme
a <- 100
b <- 150
# moyenne de l'uniforme
mu <- (a+b)/2
x <- data.frame(runif(n, min = a, max = b))
x %>%
mutate(y = ifelse(x > mu*(1-K) & x < mu*(1+K), 1, 0)) %>%
summarize(percent = 100*sum(y)/n)## percent
## 1 49.872Les simulations nous confirment ainsi le résultat mathématique que nous avons calculé. Avec une loi uniforme(\(100, 125\)), nous avons 90% des chances que \(s\) soit à plus ou moins 10% de la moyenne \(\mu_S = 112.5\), mais les chances tombent à environ 50% si nous utilisons une loi uniforme(\(100, 150\)).
Exemple 2.2 Montrez mathématiquement le résultat des dernières simulations en utilisant une loi uniforme(100,150)$.
(Exemple à faire en exercice)
2.1.2 Exemple: Loi normale
Exemple 2.3 On suppose que \(S \sim Normal(a,b^2)\). Trouvez la condition sur les paramètres \(a\) et \(b^2\) pour laquelle la variable aléatoire \(S\) respecterait le critère de stabilité d’ordre \((K, p)\).
(Exemple à faire en classe)
On peut utiliser nos connaissance du package ggplot2 pour dessiner la densité d’une loi normale, et identifier correctement ce que nous cherchons avec les quantiles reliés au critère de stabilité.
values <- data.frame(x=seq(-4, 4, by=0.1))
values$y <- dnorm(values$x)
p <- 0.90
q <- (1-p)/2
Q <- qnorm((1-p)/2, lower.tail = FALSE)
Q2 <- format(round(Q, 3), nsmall = 3)
dnorm_one_sd <- function(x){
norm_one_sd <- dnorm(x)
norm_one_sd[x < -Q| x > Q] <- NA
return(norm_one_sd)
}
ggplot() +
geom_line(data=values, aes(x = x, y=y), size=1.1)+
stat_function(fun = dnorm_one_sd, geom = "area", fill = "red", alpha = 0.3) +
geom_text(aes(x=0, y=0.15, label=paste0('p=', scales::percent(p))), size=5, show.legend = FALSE)+
geom_text(aes(x=-2, y=0.02, label=paste0('1-q=', scales::percent(q))), size=3.2, show.legend = FALSE)+
geom_text(aes(x=2, y=0.02, label=paste0('1-q=', scales::percent(q))), size=3.2, show.legend = FALSE)+
geom_text(aes(x=-Q+0.05, y=-0.015, label=paste0('-Q(q) =', format(round(-Q, 3), nsmall = 3))), show.legend = FALSE)+
geom_text(aes(x=Q-0.05, y=-0.015, label=paste0('Q(q) =', format(round(Q, 3), nsmall = 3))), show.legend = FALSE)+
geom_segment(aes(x = Q-0.05, y = 0, xend = Q-0.05, yend = dnorm(Q-0.05))) +
geom_segment(aes(x = -Q+0.05, y = 0, xend = -Q+0.05, yend = dnorm(Q-0.05))) +
geom_point(aes(x = -Q+0.05, y = 0)) +
geom_point(aes(x = Q-0.05, y = 0)) +
xlim(c(-4, 4)) +
labs(x = "\n x", y = "f(x) \n") +
theme_bw()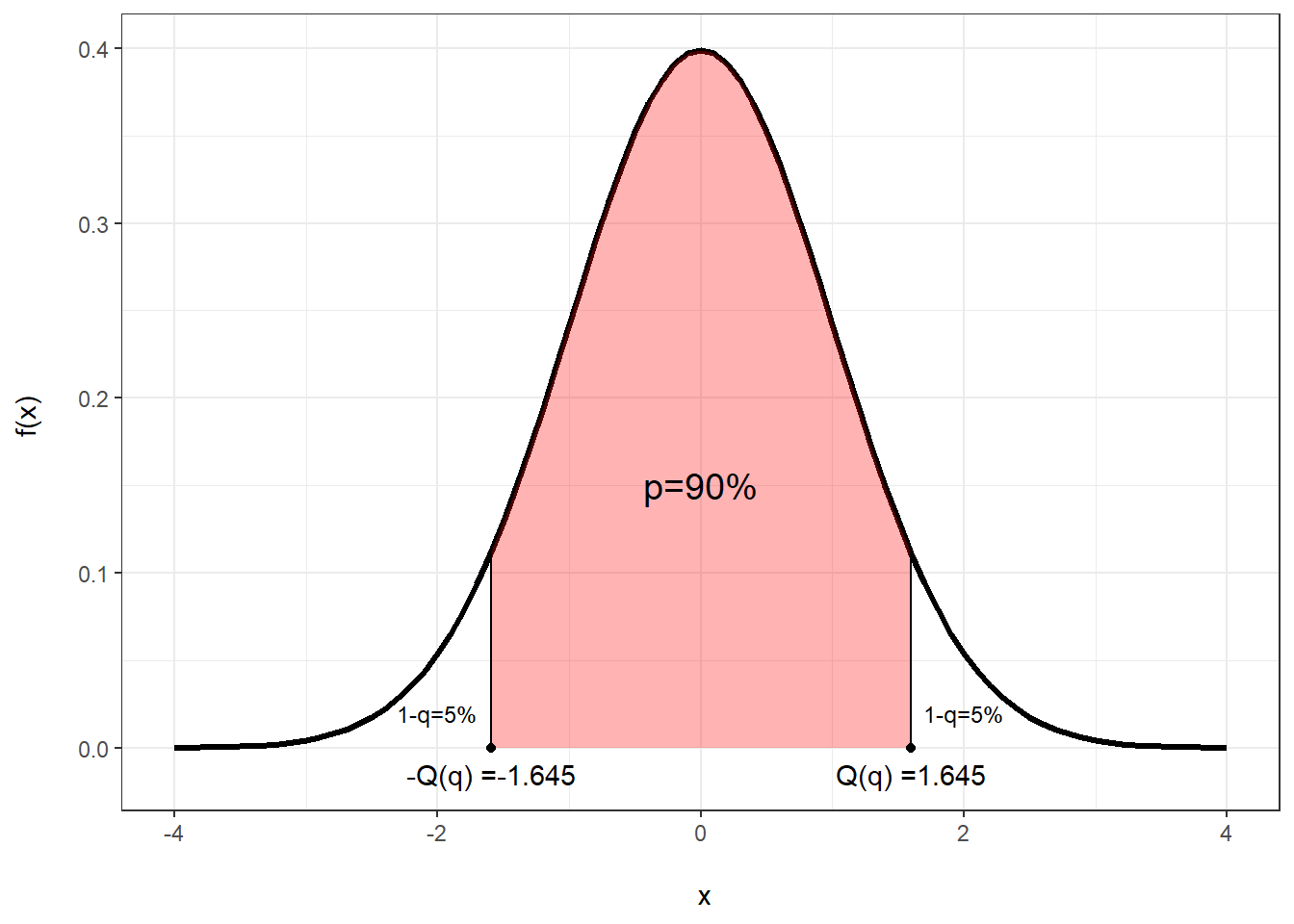
Exemple 2.4 Supposons que \(p=0.90\). Trouvez les quantiles \(Q(q)\) et \(-Q(q)\) d’une loi gaussienne centrée réduite (\(Normal(0,1)\)).
(Exemple à faire en classe)
Exemple 2.5 On suppose que \(S \sim Normal(a,b^2)\). Quelle est la condition sur \(a\) et \(b\) pour que la variable aléatoire \(S\) respecte le critère de stabilité d’ordre \((K=0.05, p=0.9)\).
(Exemple à faire en classe)
Cela signifie que si on tirait au hasard une réalisation \(s\) d’une loi \(Normale(a,b^2)\) satisfaisant
\[\left( \frac{a}{b} \right)^2 \ge 1082, \]
nous serons certains à \(90\%\) que \(s\) serait située entre \(0.95\) et \(1.05\) fois la moyenne \(a\).
Exemple 2.6 On suppose que \(S \sim Normal(1000,b^2)\). Quelle est la condition sur \(b\) pour que la variable aléatoire \(S\) respecte le critère de stabilité d’ordre \((K=0.05; p=0.9)\).
(Exemple à faire en classe)
Il est encore une fois possible de vérifier les résultats mathématiques obtenus en passant par la simulation.
# initialisation du générateur de nombres aléatoires
set.seed(42)
# paramètres de la loi normale
a <- 1000
# critères de stabilité
K <- 0.05
p <- 0.90
Qq <- qnorm((1-p)/2, lower.tail = FALSE)
borne <- Qq/K
(b <- a/borne)## [1] 30.39784 # nb de simulations
n <- 1000000
x <- data.frame(rnorm(n, mean=a, sd=b))
x %>%
mutate(y = ifelse(x > a*(1-K) & x < a*(1+K), 1, 0)) %>%
summarize(percent = 100*sum(y)/n) ## percent
## 1 89.9645Vérifions ce que serait l’impact d’une augmentation de 10% de la valeur de \(b\).
x <- data.frame(rnorm(n, mean=a, sd=b*1.1))
x %>%
mutate(y = ifelse(x > a*(1-K) & x < a*(1+K), 1, 0)) %>%
summarize(percent = 100*sum(y)/n) ## percent
## 1 86.5496Exemple 2.7 Montrez mathématiquement le résultat précédent, avec une augmentation de 10% de la valeur de \(b\).