4.2 Hétérogénéité
On réfère souvent au terme d’hétérogénéité lorsqu’on parle de ces catégories invisibles, du type bon ou mauvais conducteur.
Formellement, on rend compte de l’hétérogénéité en introduisant un effet aléatoire \(\Theta\) (par exemple, le fait d’être un conducteur \(b\) ou \(m\)), et \(\Theta\) représente le niveau de risque inconnu de l’assuré.
La présence d’hétérogénéité dans un portefeuille d’assurance fait en sorte que le profil du conducteur devient lui aussi une variable aléatoire.
Exemple 4.4 On pourrait donc formaliser l’exemple des bons et mauvais conducteurs en introduisant un effet aléatoire \(\Theta\) pour remplacer le type de conducteurs \(C\). Dans un tel cas, on dira que le portefeuille d’assurance se divise en \(2\) types de conducteurs avec \(N_t|\Theta=\theta \sim Poisson(\theta)\) et:
| Profils | #1 | #2 |
|---|---|---|
| \(\Theta\) | \(\theta_1\) | \(\theta_2\) |
| \(\Pr(\Theta=\theta)\) | \(p_1\) | \(p_2\) |
En exercice, refaites l’exemple avec la nouvelle notation.
(Exemple à faire en classe)
Les résultats obtenus dans l’exemple des conducteurs seront toujours valides, seule la notation et l’écriture du problème auront changé.
Exemple 4.5 On généralise le problème et on suppose maintenant que le portefeuille d’assurance se divise en \(J\) types de conducteurs. Ainsi, nous avons \(N_t|\Theta=\theta \sim Poisson(\theta)\) et:
| Profils | #1 | #2 | \(\ldots\) | #J |
|---|---|---|---|---|
| \(\Theta\) | \(\theta_1\) | \(\theta_2\) | \(\ldots\) | \(\theta_J\) |
| \(\Pr(\Theta=\theta)\) | \(p_1\) | \(p_2\) | \(\ldots\) | \(p_J\) |
Montrez que:
- La distribution de l’hétérogénéité \(\Theta\), sachant \(N_1=n_1, \ldots, N_{T} =n_{T}\), s’exprime comme:
\[ \Pr[\Theta=\theta_k|N_1=n_1, \ldots, N_{T} =n_{T}] = \frac{\exp(-T \theta_k) \theta_k^{\sum_{t=1}^{T} n_t} p_k} {\sum_{j=1}^J \exp(-T \theta_j) \theta_j^{\sum_{t=1}^{T} n_t} p_j}, \forall k \in {1, \ldots, J}.\]
- La forme de la prime prédictive s’exprime comme:
\[ E[N_{T+1}|N_1=n_1, \ldots, N_{T} =n_{T}] = \frac{\sum_{j=1}^J \theta_j \exp(-T \theta_j) \theta_j^{\sum_{t=1}^{T} n_t} p_j} {\sum_{j=1}^J \exp(-T \theta_j) \theta_j^{\sum_{t=1}^{T} n_t} p_j}.\]
(Exemple à faire à la maison)
Il peut être intéressant de voir un peu plus concrètement ce genre de modèle. Ainsi, pour \(N_t|\Theta=\theta \sim Poisson(\theta)\), on peut supposer \(J\) types de conducteurs différents, avec:
| Profils | #1 | #2 | \(\ldots\) | #j | \(\ldots\) | #J |
|---|---|---|---|---|---|---|
| \(\Theta\) | \(\frac{1}{2J}\) | \(\frac{2}{2J}\) | \(\ldots\) | \(\frac{j}{2J}\) | \(\ldots\) | \(\frac{J}{2J}\) |
| \(\Pr(\Theta=\theta)\) | \(\frac{1}{J}\) | \(\frac{1}{J}\) | \(\ldots\) | \(\frac{1}{J}\) | \(\ldots\) | \(\frac{1}{J}\) |
Les graphiques ci-dessous illustrent l’évolution de la prime d’assurance d’un assuré en fonction de son historique de sinistres sur 10 ans pour \(J \in \{2,5,10, 20\}\).
Les lignes pointillées bleues représentent chaque \(\lambda_j, j=1,\ldots, J\), alors que la ligne pointillée rouge représente la prime a priori.
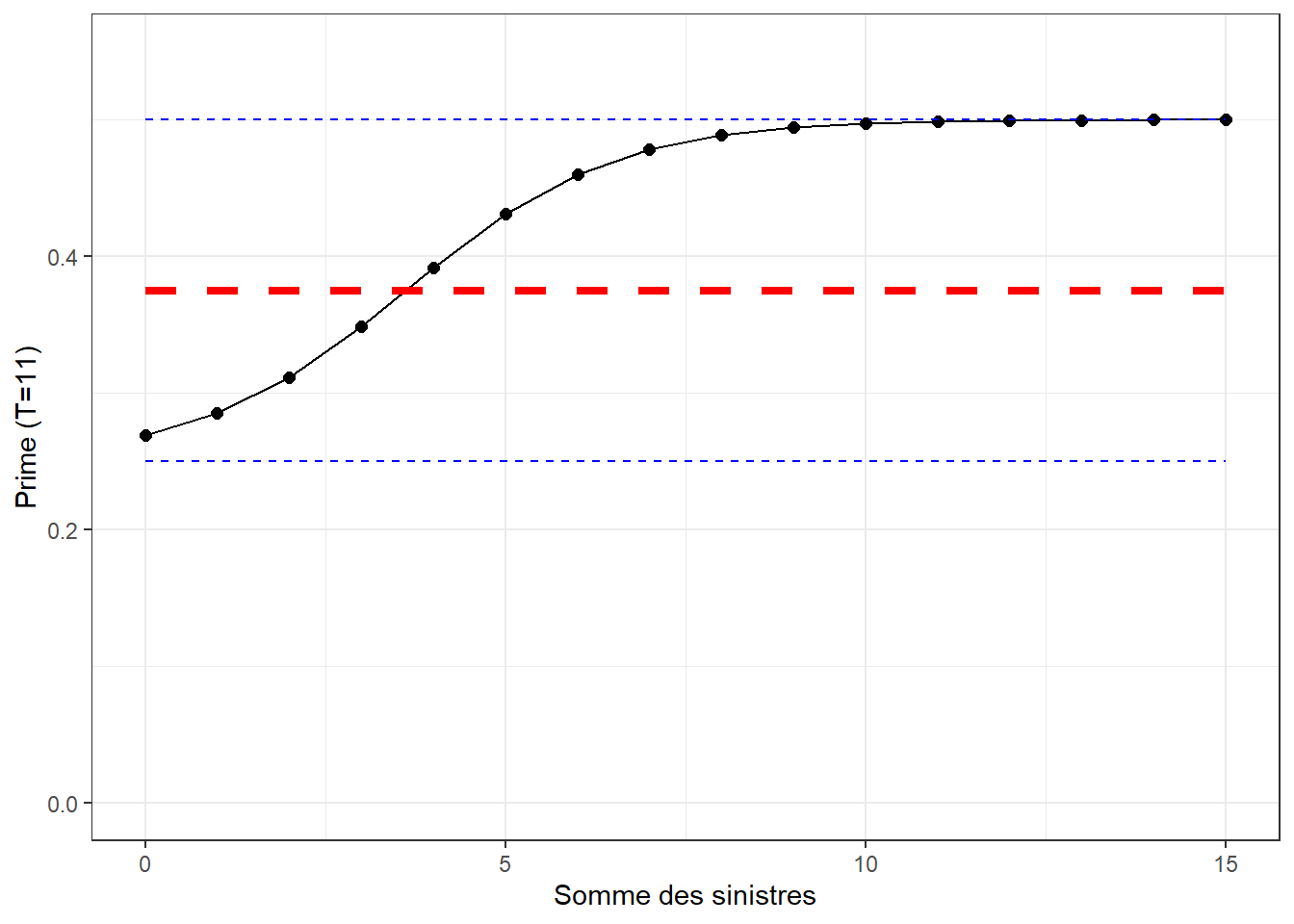
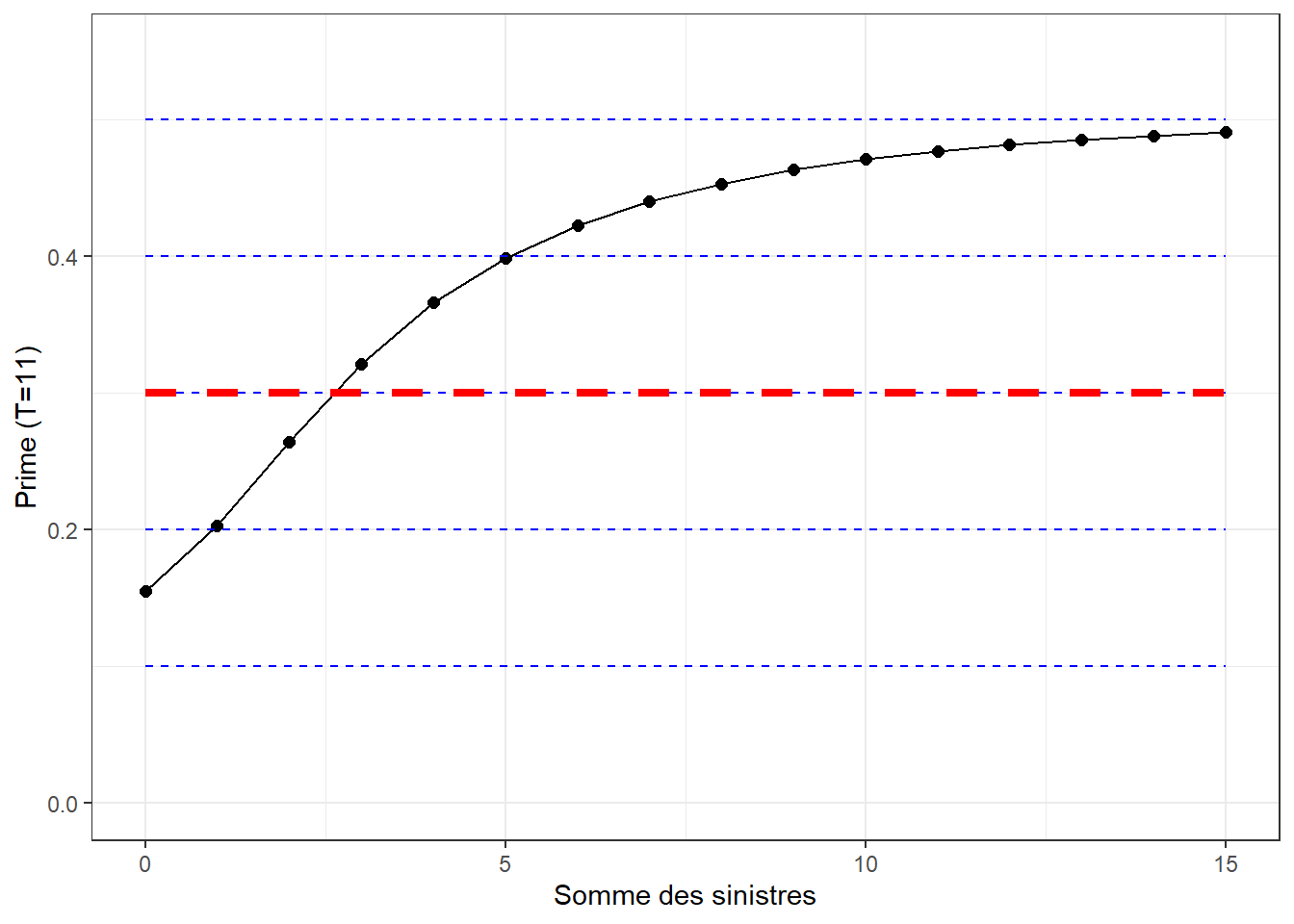

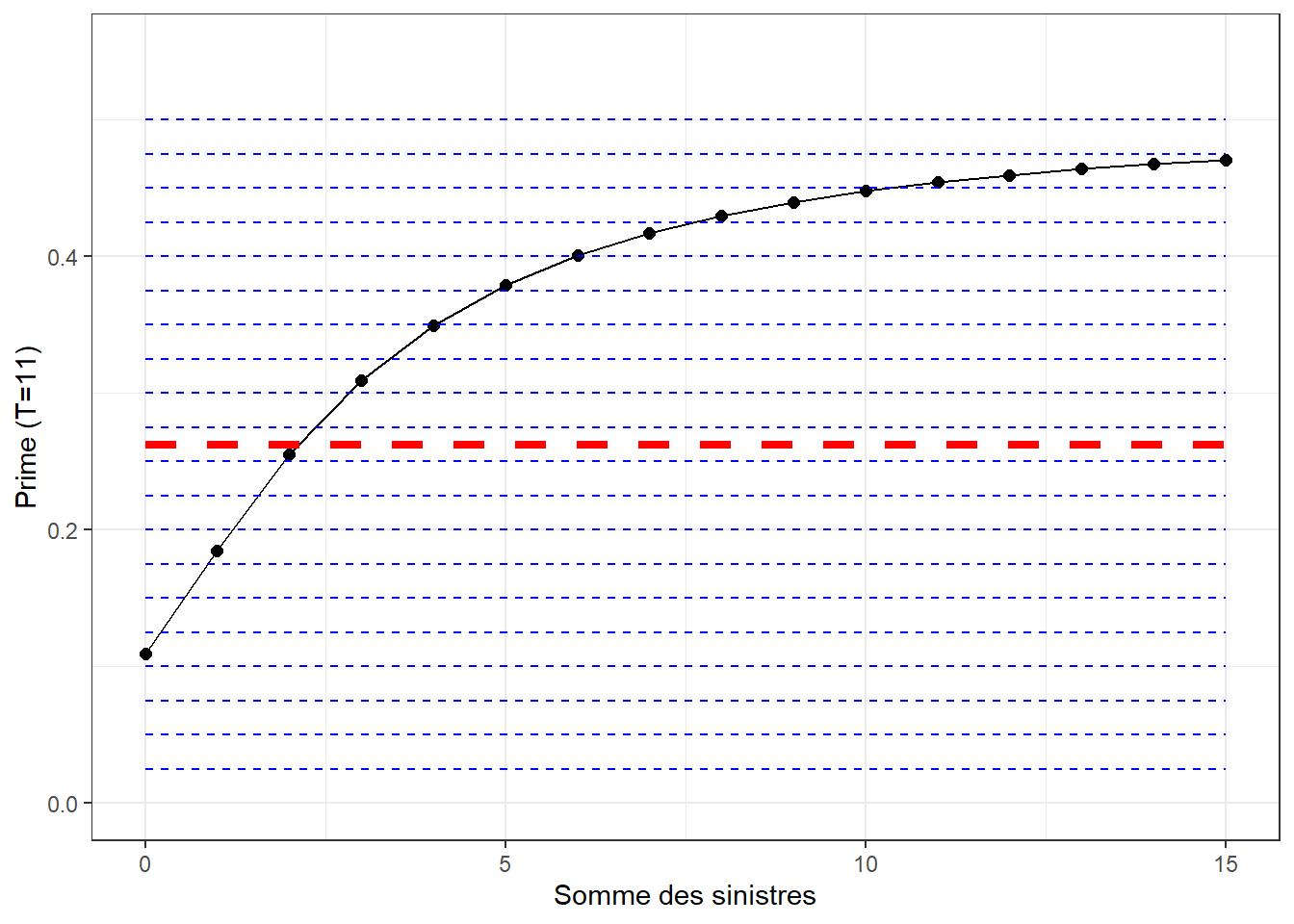
Exercice 4.1 En exercice informatique, écrivez un code informatique qui calcule la prime prédictive pour n’importe quel temps \(T\) et n’importe quel nombre de profils \(J\). De plus, générez les mêmes figures que celles ci-dessus.