6.2 Coefficient de crédibilité de Bühlmann
Le modèle de Bühlmann (dans un article publié en 1967) peut être vu comme une alternative aux modèles bayésiens. L’approche de Bühlmann est en effet basée sur les mêmes hypothèses générales que le modèle de crédibilité bayésien, à savoir
- qu’il existe une forme d’hétérogénéité dans le portefeuille, et
- que la dépendance entre les réalisations d’un même assuré \(i\) provient uniquement d’une hétérogénéité cachée notée ici \(\Theta\).
L’idée du modèle de crédibilité de Bühlmann est de restreindre, pour un assuré \(i\), la prime prédictive à avoir une forme linéaire. Plus précisément, nous cherchons à ce que la prime ait la forme suivante
\[p_{i,T+1} = \mathsf{Z} \times \overline{S_{i}} + b\]
avec \(\overline{S_i} = \frac{1}{T}\sum_{t=1}^T S_{i,t}\), la moyenne des réclamations de l’assuré pour ses périodes passées, soit \(t=1, \ldots, T\).
Proposition 6.1 Les paramètres \(\mathsf{Z}\) et \(b\) qui minimisent la fonction \(E\left[\left((\mathsf{Z}\overline S_i + b) - S_{i,T+1} \right)^2\right]\) sont:
\[\begin{eqnarray*} \mathsf{Z} &=& \frac{Cov[\overline{S}_i, S_{i,T+1}]}{Var[\overline{S}_i]}, \ \text{ et } \ b = (1-\mathsf{Z}) \mu \end{eqnarray*}\]
et la prime \(p_{i,T+1}\) s’exprime comme:
\[p_{i,T+1} = \mathsf{Z} \overline{S} + (1-\mathsf{Z}) E[\mu(\Theta)]\]
(Développement à faire en classe)
6.2.1 Paramètres de structure
On débute avec la notation suivante pour l’espérance conditionnelle et la variance conditionnelle:
\[\begin{eqnarray*} \mu(\Theta) &=& E[S_{i,t}|\Theta] \\ \sigma^2(\Theta) &=& Var[S_{i,t}|\Theta] \end{eqnarray*}\]
Dans le chapitre sur la crédibilité bayésienne, nous avions vu que la prime de risque \(\mu(\Theta)\) est une fonction \(\mu()\) qui dépend uniquement de son argument \(\Theta\), et que la prime de risque ne dépend ni de \(t\), ni de \(i\).
La même remarque s’applique à \(\sigma^2(\Theta)\): il s’agit d’une fonction \(\sigma^2()\) qui dépend uniquement de son argument \(\Theta\), et ne dépend ni du contrat \(t\), ni de l’assuré \(i\).
On peut aussi profiter de l’occasion pour rappeler l’important résultat concernant la covariance conditionnelle, et impliquant l’indépendance conditionnelle, soit que:
\[\begin{eqnarray*} Cov[S_{i,t}, S_{i,s}|\Theta] = 0 \text{, pour } s \ne t. \end{eqnarray*}\]
En d’autres mots, lorsque le paramètre d’hétérogénéité \(\Theta\) est connu, les variables aléatoires \(S_{i,t}\) et \(S_{i,s}\) sont indépendantes pour \(s \ne t\).
Par la suite, afin d’obtenir la prime de crédibilité du modèle de Bühlmann, il suffit de développer une séries de résultats qui seront nécessaires aux calculs du coefficient de crédibilité \(\mathsf{Z}\).
6.2.1.1 Définitions
Définition 6.1 La moyenne a priori (correspondant aussi à la prime a priori, ou à la prime collective) est donnée par:
\[\begin{eqnarray*} \mu = E[S_{i,t}] = E[\mu(\Theta)] \end{eqnarray*}\]
Définition 6.2 La moyenne des variances individuelles, ou en anglais expected value of process variance, et donc souvent notée EPV, correspond à:
\[\Sigma^2 = E[\sigma^2(\Theta)]\]
Définition 6.3 La variance des moyennes individuelles, ou en anglais variance of the hypothetical mean, et donc souvent notée VPH, correspond à:
\[M^2 = Var[\mu(\Theta)]\]
Proposition 6.2 La variance a priori , notée \(\sigma^2\), se décompose donc comme:
\[\begin{eqnarray*} \sigma^2 = Var[S_{i,t}] &=& E[Var(S_{i,t}|\Theta)] + Var[E(S_{i,t}|\Theta)]\\ &=& E[\sigma^2(\Theta)] + Var[\mu(\Theta)]\\ &=& \Sigma^2 + M^2 \end{eqnarray*}\]
6.2.1.2 Covariances
En ayant définis quelques termes, il est possible de calculer la covariance entre plusieurs termes, ou variables aléatoires du modèles de crédibilité de Bühlmann.
Proposition 6.3 La covariance entre les montants annuels \(S_{i,t}\) et \(S_{i,s}\) s’exprime comme:
\[\begin{align*} Cov(S_{i,t},S_{i,s}) &=& \begin{cases} & \Sigma^2 + M^2, \ \ \ \text{ si } s = t \\ & M^2, \ \ \ \ \ \ \ \ \ \ \ \ \text{ si } s \ne t \end{cases} \end{align*}\]
(Développement à faire en classe)
Corollaire 6.1 La covariance entre les montants annuels \(S_{i,t}\) et \(S_{i,T+1}\), (pour \(T+1 \ne t\)), s’exprime comme:
\[Cov(S_{i,t}, S_{i,T+1} ) = M^2\]
Proposition 6.4 La covariance entre la moyenne des montants annuels \(S_{i,t}\) pour \(t=1, \ldots, T\), notée \(\overline{S}_{i}\), et \(S_{i,T+1}\) s’exprime comme:
\[ Cov(\overline{S}_{i}, S_{i,T+1} ) = M^2\]
(Développement à faire en classe)
Proposition 6.5 La variance de la moyenne des montants annuels \(S_{i,t}\) pour \(t=1, \ldots, T\), notée \(\overline{S}_{i}\) s’exprime comme:
\[ Var(\overline{S}_{i}) = \frac{1}{T} \Sigma^2 + M^2 \]
(Développement à faire en classe)
6.2.2 Exemples
La crédibilité de Bühlmann s’applique assez facilement avec des modèles paramétriques.
Exemple 6.1 On suppose que le coût total des réclamations annuelles d’un assuré \(i\) suit une loi normale de moyenne \(\theta\) et de variance \(100,000\). Formellement, nous avons ainsi
\[S_{i,t} |\Theta = \theta \sim Normal(\theta, \sigma^2 = 100,000).\]
Les actuaires pensent qu’il existe 3 types d’assurés dans le portefeuille
\[\begin{eqnarray*} \Pr(\Theta = \theta) = \begin{cases} 0.2, \ \text{pour } \theta=100\\ 0.3, \ \text{pour } \theta=500\\ 0.5, \ \text{pour } \theta=1000\\ \end{cases}, \end{eqnarray*}\]
- Calculez la valeur du coefficient \(\mathsf{Z}\) pour ce modèle;
- Calculez la prime qu’on offrirait à un nouvel assuré sans expérience;
- Si l’expérience observée au cours des trois dernières années était \(s_1 = 230; s_2 = 120; s_3 = 400\), trouvez la prime de crédibilité de Bühlmann pour l’année 4.
(Exemple à faire en classe)
Exemple 6.2 On reprend le même exemple, mais on suppose maintenant que les coûts ne suivent pas une normale, mais plutôt une exponentielle de moyenne \(\Theta\). On garde la même distribution des types d’assurés dans le portefeuille. Répondez de nouveau aux questions suivantes:
- Calculez la valeur du coefficient \(\mathsf{Z}\) pour ce modèle;
- Calculez la prime qu’on offrirait à un nouvel assuré sans expérience;
- Si l’expérience observée au cours des trois dernières années était \(s_1 = 230; s_2 = 120; s_3 = 400\), trouvez la prime de crédibilité de Bühlmann pour l’année 4.
(Exemple à faire en classe)
On peut comparer la précision de la prime de crédibilité de Bühlmann, et la comparant avec la prime de crédibilité bayésienne.
set.seed(123)
## paramètres
p <- c(0.2,0.3,0.5)
theta <- c(100,500,1000)
sigma2 <- 100000
std <- sqrt(sigma2)
nsimul <- 10000
all.result <- data.frame()
for(i in 1:nsimul){
rand <- runif(1, 0, 1)
type <- ifelse(rand < p[1], theta[1], ifelse(rand < p[1]+p[2], theta[2], theta[3]))
normal <- c(rnorm(1, type, std), rnorm(1, type, std),rnorm(1, type, std))
expo <- c(rexp(1, 1/type), rexp(1, 1/type),rexp(1, 1/type))
### normal ###
p1 <- dnorm(normal[1], theta[1], std)*dnorm(normal[2], theta[1], std)*dnorm(normal[3], theta[1], std)
p2 <- dnorm(normal[1], theta[2], std)*dnorm(normal[2], theta[2], std)*dnorm(normal[3], theta[2], std)
p3 <- dnorm(normal[1], theta[3], std)*dnorm(normal[2], theta[3], std)*dnorm(normal[3], theta[3], std)
prob1 <- p1*p[1]/(p1*p[1]+p2*p[2]+p3*p[3])
prob2 <- p2*p[2]/(p1*p[1]+p2*p[2]+p3*p[3])
prob3 <- p3*p[3]/(p1*p[1]+p2*p[2]+p3*p[3])
priori.norm <- p[1]*theta[1]+p[2]*theta[2]+p[3]*theta[3]
pred.norm <- prob1*theta[1]+prob2*theta[2]+prob3*theta[3]
Z.norm <- 3/(3 + sigma2/128100)
X.bar <- (normal[1]+normal[2]+normal[3])/3
buhl.norm <- Z.norm * X.bar + (1-Z.norm)*priori.norm
##
result1 <- cbind(i, type, calcul="Bayes", value = pred.norm)
result2 <- cbind(i, type, calcul="Bühlmann", value = buhl.norm)
all.result <- rbind(all.result, result1, result2)
}
all.result$type <- factor(all.result$type, levels=c('100', '500', '1000'))
ggplot(all.result, aes(x=calcul, y=as.numeric(value), fill=calcul))+
geom_boxplot(show.legend = FALSE)+
labs(y = "Prediction", x = ".") +
facet_wrap(~type) +
theme_bw()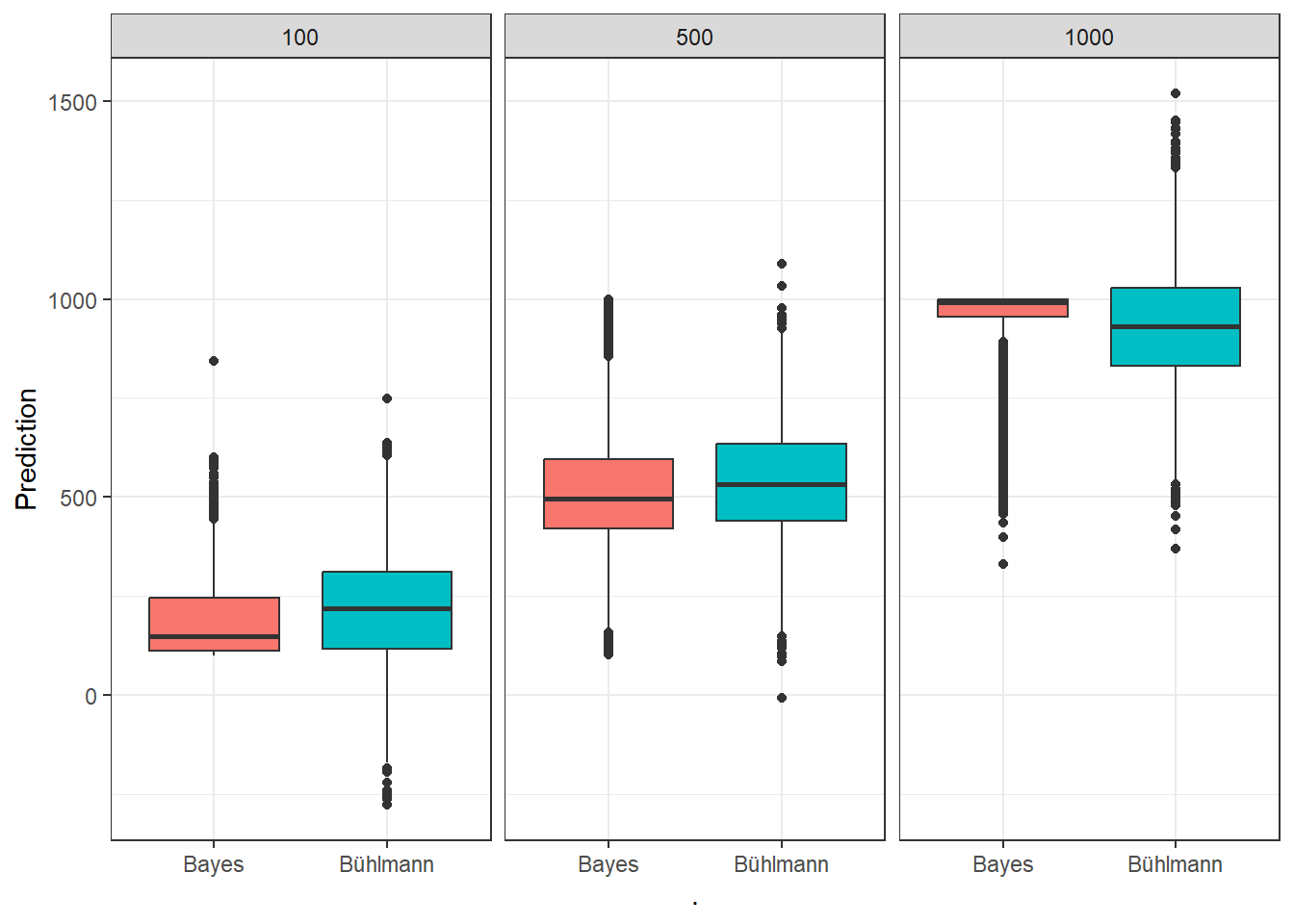
Quelques remarques sur la simulation:
L’approximation par Bühlmann est beaucoup plus simple et rapide que le long calcul bayésien
Le modèle de Bühlmann semble produire des résultats satisfaisants, comparativement au calcul exact par le théorème de Bayes;
Même l’approche bayésienne peut parfois se tromper: on voir en effet que dans certaines situations, la prime prédictive était loin de la vraie valeur de \(\Theta\);
Contrairement à l’approche bayésienne, il n’y aucunes limites inférieure ou supérieure à la valeur de la prime de crédibilité de Bühlmann. Alors que la prime bayésienne est limitée à être entre \(100\) et \(1000\) (le plus petit et le plus grand \(\theta\)), la prime de crédibilité de Bühlmann peut proposer des primes inférieures à \(100\) ou supérieure à 1000. La prime ne propose en effet aucune limite puisque sa forme est:
\[p_{i,T+1} = \mathsf{Z} \overline{S} + (1-\mathsf{Z}) E[\mu(\Theta)]\]
Exercice 6.1 Faites une comparaison, en R, entre le modèle de crédibilité de Bühlmann et la crédibilité bayésienne, pour le dernier exemple qui utilisait une loi exponentielle pour les coûts.
6.2.3 Analyse du coefficient de crédibilité
Nous avons déterminé que le coefficient \(\mathsf{Z}\) du modèle de la crédibilité de Bühlmann était égal à :
\[\begin{eqnarray*} \mathsf{Z} &=& \frac{T}{K + T}, \text{ où } K = \frac{\Sigma^2}{M^2} = \frac{E[\sigma^2(\Theta)]}{Var[\mu(\Theta)]} \end{eqnarray*}\]
On peut voir que trois éléments influencent la valeur de \(\mathsf{Z}\), soit \(T\), \(\Sigma^2\) et \(M^2\). Il est intéressant de comprendre de quelle manière chacun des ces éléments font augmenter ou diminuer le poids qu’on accorde à l’expérience individuelle dans le calcul d’une prochaine réalisation de la variable aléatoire.
6.2.3.1 Le nombre d’observations passées, \(T\)
Lorsque \(T=0\), cela signifie que nous n’avons pas d’observations passées pour ajuster notre connaissance a priori de l’hétérogénéité \(\Theta\). Ainsi, il est logique que \(\mathsf{Z}\) soit égal à 0 dans ce cas.
À l’inverse, on peut voir que lorsque \(T\) augmente, nous avons de plus en plus d’observations nous permettant de mieux connaitre le profil de risque, et estimer la valeur du paramètre d’hétérogénéité \(\Theta\). Ainsi, lorsque \(T \rightarrow \infty\), nous avons aussi \(\mathsf{Z} \rightarrow 1\).
Puisque nous avons la forme de prime suivante:
\[p_{i,T+1} = \mathsf{Z} \overline{S} + (1-\mathsf{Z}) E[\mu(\Theta)],\]
une convergence de \(\mathsf{Z} \rightarrow 1\) implique que \(p_{i,T+1} \rightarrow \overline{S}\) signifiant que la prime future sera simplement égale à l’expérience moyenne individuelle.
6.2.3.2 Les paramètres \(\Sigma^2\) et \(M^2\)
Il convient d’analyser conjointement les deux paramètres \(\Sigma^2\) et \(M^2\) pour comprendre de quelle manière ils ont une influence sur le facteur de crédibilité \(\mathsf{Z}\).
Puisque nous avons \(\mathsf{Z} = \frac{T}{K + T}\), nous savons:
- qu’une grande valeur de \(K\) diminue le poids accordé à l’expérience individuelle,
- qu’une petite valeur de \(K\) augmente le poids accordé à l’expérience individuelle.
Alors, avec \(K= \frac{\Sigma^2}{M^2}\), on sait donc que:
- une grande valeur de \(\Sigma^2\) diminuera le poids accordé à l’expérience individuelle (ou inversement, augmentera),
- une grande valeur de \(M^2\) augmentera le poids accordé à l’expérience individuelle (ou inversement, diminuera).
Mais il n’est pas si intuitif de comprendre pourquoi nous avons ce résultat, ni ce que cela signifie.
Le paramètre \(\Sigma^2\) représente la moyenne des variances, sachant le profil de risque. Si la valeur de \(\Sigma^2\) est petite, cela signifie que l’expérience de sinistre d’un profil de risque précis, ne varie pas beaucoup. Il est plus simple d’identifier un profil de risque si les réalisations de ce profil de risque sont similaires, et la crédibilité accordée èa l’expérience passée sera élevée.
Le paramètre \(M^2\) représente la variance de l’espérance, sachant le profil de risque. Si la valeur de \(M^2\) est très élevée, cela signifie que les profils de risque du portefeuille sont différents les uns des autres. Il est donc plus facile d’associer un historique de sinistres a un profil précis, et la crédibilité accordée èa l’expérience passée sera élevée.
Pour mieux illustrer l’impact de \(\Sigma^2\) et \(M^2\) sur le facteur de crédibilité et l’importance qu’on accorde à l’expérience individuelle pour prévoir une prochaine réalisation aléatoire, supposons des joueurs de dards qui lancent vers une cible. Chacun des joueurs vise une cible en particulier, et on essaie de prévoir l’endroit d’un prochain lancer et se basant, ou non, sur les lancers précédents de cette personne.
Supposons ainsi 3 joueurs, et débutons nos simulations avec
une petite valeur de \(\Sigma^2\) et
une grande valeur de \(M^2\).
Dans un tel cas, tel que nous venons de le voir, le coefficient \(\mathsf{Z}\) serait très élevé, signifiant qu’on se baserait beaucoup sur l’expérience individuelle pour prévoir l’endroit d’un prochain lancer. Le graphique plus bas illustre une telle situation.
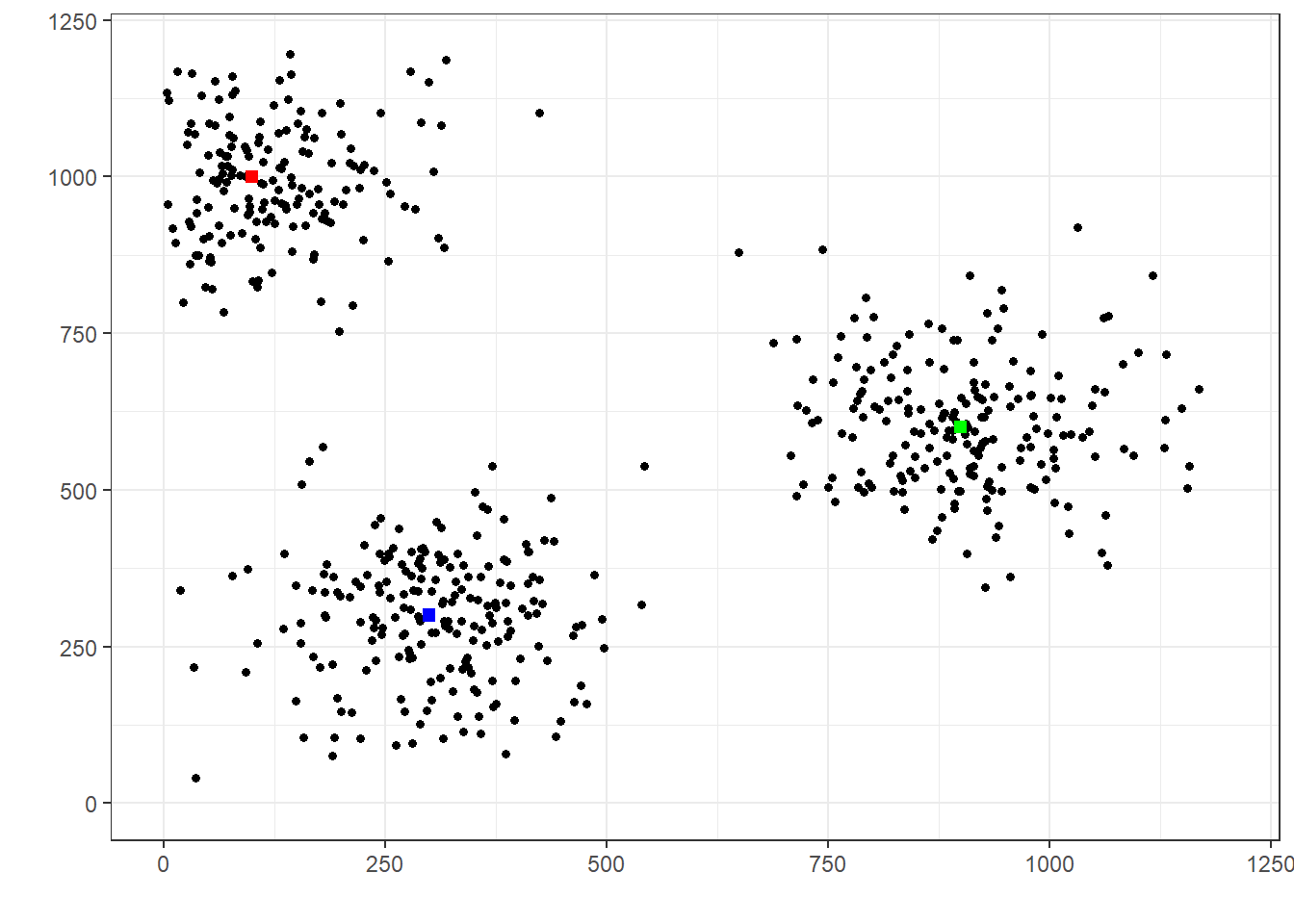
La cible de chacun des lanceurs est identiée par les trois carrés rouge, bleu et vert.
On voit qu’il est assez simple d’associer chaque lancer à une cible et donc à un lanceur. Ainsi, en se basant sur les lancers précédents d’une personne, il serait relativement simple de prévoir où son prochain lancer sera. Le facteur de crédibilité est élevé dans une telle situation.
Maintenant, modifions les paramètres de la simulation et augmentons \(\Sigma^2\) représentant la moyenne des variances, sachant le profil de risque.
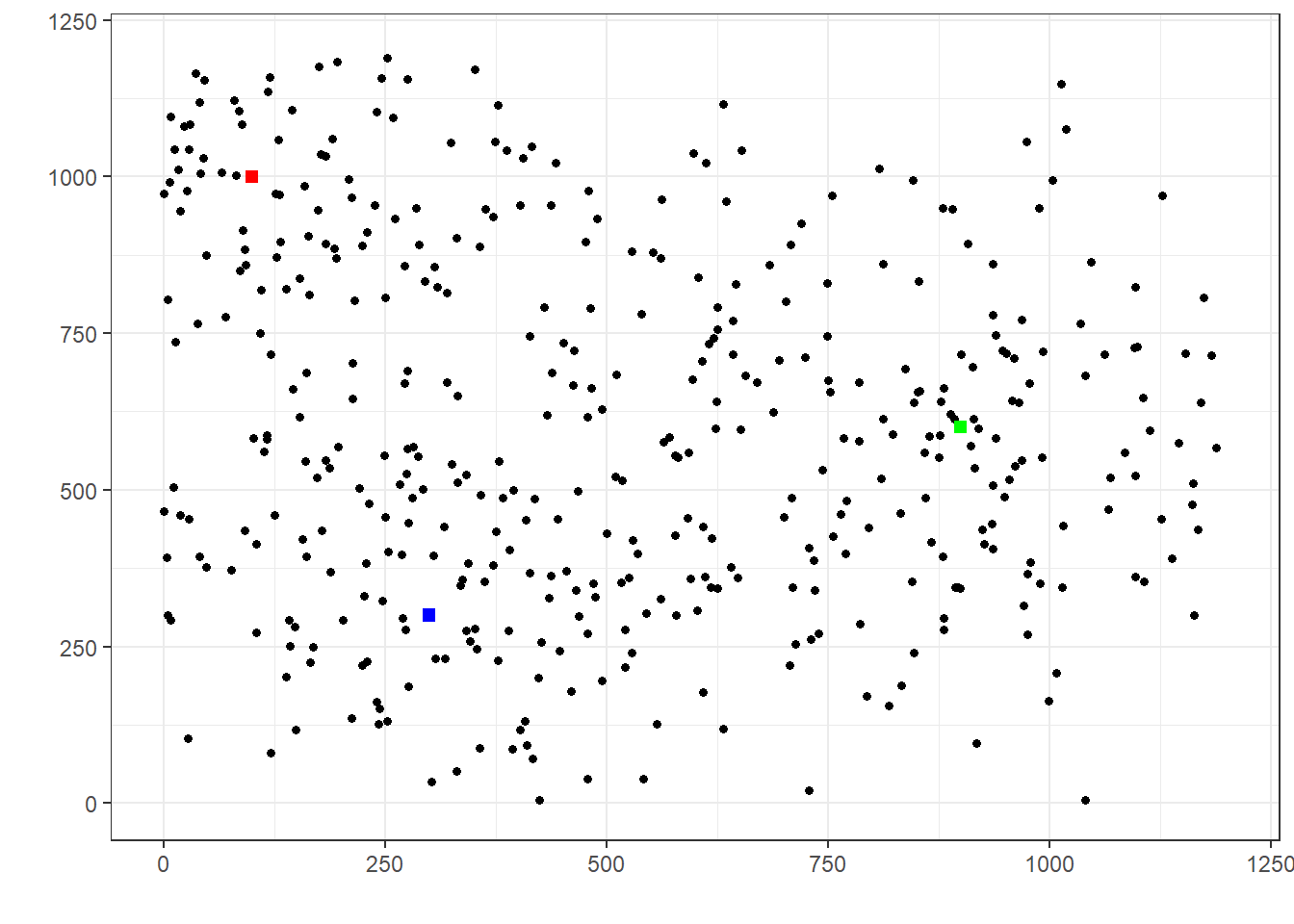
En analysant le graphique, on peut voir qu’il devient beaucoup plus difficile d’associer un lancer particulier à l’une des trois cibles. Ainsi, si on veut prévoir le prochain lancer d’une personne, se baser sur ses lancers précédents nous donne moins d’information que dans le premier graphique. En d’autres mots, on accordera moins de crédibilité aux résultats passés pour prévoir l’endroit du prochain lancer.
Comme dernière illustration, revenons avec la valeur de \(\Sigma^2\) initiale, mais diminuons maintenant \(M^2\), la variance de l’espérance, sachant la profil de risque.
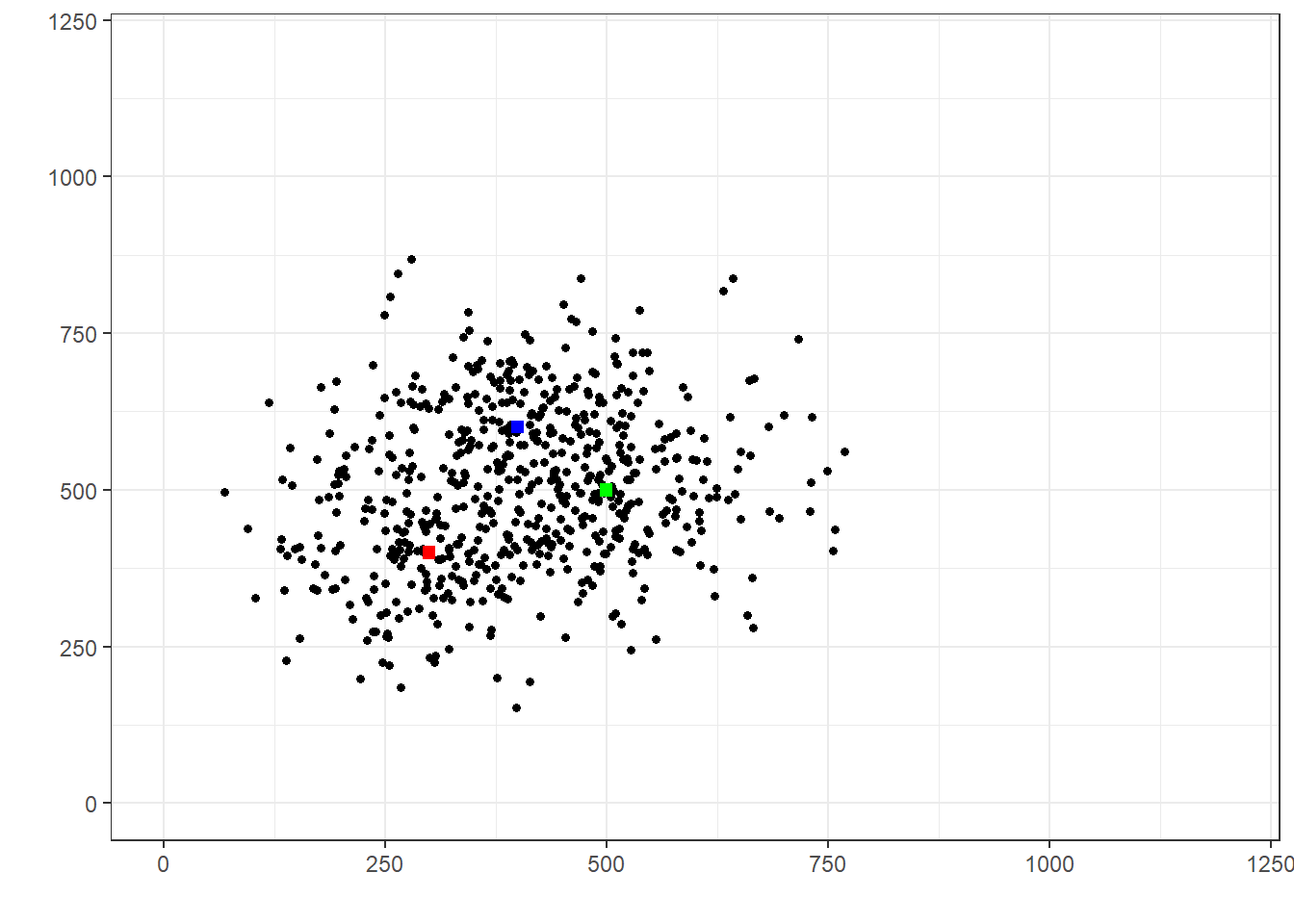
Dans ce cas-ci, même si \(\Sigma^2\) est revenu à son niveau initial, on voit malgré tout qu’il devient difficile d’associer chaque lancer à une cible, simplement parce que les cibles sont proches, donc similaires. Dans un tel cas, comparativement à la première simulation, nous accorderons moins d’importance à l’expérience individuelle pour le prévision d’un prochain lancer.