3.3 Crédibilité partielle
Les actuaires reprennent la même astuce qu’en crédibilité complète pour passer d’un critère de stabilité à une utilisation de la crédibilité pour une observation \(s\). Par contre, quelques ajustements doivent être fait dans le cas d’une crédibilité partielle.
Proposition 3.6 L’expérience de sinistre observée \(s\) a une crédibilité partielle \(\mathsf{Z}\) d’ordre \((K,p)\) si elle provient d’une variable aléatoire \(S\) respectant la relation exprimée par l’équation de la proposition 3.2.
Exemple 3.6 On reprend l’exemple des constructeurs automobiles. Les actuaires supposent que la variable aléatoire \(S\) modélisant la charge totale de réclamations de Bombardieret celle pour Pangloss Automobile suit une Poisson composée, avec \(N \sim Poisson(\lambda)\) et \(X_i \sim Exponentiel(\beta)\).
L’historique de sinistre des deux constructeurs, et celui de l’industrie, sont résumés dans le tableau suivant:
| Cie. | Charge pure | Nb. de sin. |
|---|---|---|
| Bombardier | 12.51 | 3,251 |
| Pangloss | 11.49 | 983 |
| Industrie | 18.23 | 49,486 |
Dans l’exemple au chapitre de la crédibilité complète, nous avons vu que
Pour la stabilité d’ordre \((K = 0.05, p=0.90)\), \(\lambda_{cc} = 2164\);
Puisque \(3251 > 2164\), l’historique de réclamations de Bombardierest stable et une crédibilité de 100% était accordée à son expérience de réclamation.
Quelle crédibilité accorderait-on à l’expérience de réclamation de Pangloss Automobile?
(Exemple à faire en classe)
3.3.1 Complément de crédibilité
Nous savons ce qu’implique la valeur de \(\mathsf{Z} < 100\%\) au niveau de la stabilité de la variable aléatoire \(S\). Par contre, pour la crédibilité et la tarification, que voudrait dire l’expression “accorder \(\mathsf{Z}\) de crédibilité à l’expérience d’un assuré”?
Exemple 3.7 La charge pure observée de Pangloss Automobile est de \(11.49\) par employé, et nous venons de voir dans l’exemple précédent que pour un ordre \(K = 0.05, p=0.90)\), nous accorderions une crédibilité de \(\mathsf{Z} = 67.39\%\) à son expérience individuelle.
Il ne ferait pas de sens de tarifer Pangloss Automobile à un taux de \(\mathsf{Z} \times 11.49 = 7.74\), soit une prime encore plus basse que si on considérait son expérience de sinistres totalement crédible.
Afin d’obtenir une prime d’assurance, un complément de crédibilité, noté \(\mu_{comp}\), doit être ajouté en complément de \((1-\mathsf{Z})\) à l’expérience de sinistre crédibilisé \(\mathsf{Z} s\). La plupart du temps, le complément de crédibilité \(\mu_{comp}\) correspond à l’expérience observée du portefeuille d’assurance en entier, ce qui souvent appelé prime collective.
Proposition 3.7 Une prime crédibilisée s’exprime comme:
\[\text{Prime} = \mathsf{Z} s + (1-\mathsf{Z}) \mu_{comp} \]
Exemple 3.8 En poursuivant l’exemple des constructeurs automobiles, proposez une prime crédibilisée pour Pangloss Automobile.
(Exemple à faire en classe)
Il pourrait être intéressant d’analyser la prime crédibilisée de Pangloss Automobile en fonction de son nombre de réclamations observés.
# critères de stabilité
K <- 0.05
p <- 0.95
# charge pure observée
mu_pangloss <- 11.49
mu_comp <- 18.23
values <- data.frame(nb.sin=seq(0, 2500, by=1))
values$Z <- pmin(sqrt(values$nb.sin/2164),1)
values$Prime <- values$Z*mu_pangloss + (1-values$Z)*mu_comp
ggplot() +
geom_line(data=values, aes(x = nb.sin, y=Prime), size=1)+
geom_point(data=values, aes(x = 983, y=values[984,3]), size=3, color='red')+
geom_point(data=values, aes(x = 983, y=0), size=3, color='red')+
geom_text(aes(x=2000, y=19, label='Charge pure industrie'), color='blue', show.legend = FALSE)+
geom_text(aes(x=500, y=11, label='Charge pure Pangloss'), color='blue', show.legend = FALSE)+
geom_text(aes(x=1100, y=14.5, label= format(round(values[984,3], 2), nsmall = 2)), color='red', show.legend = FALSE)+
geom_segment(aes(x = 0, xend = 2500, y = mu_comp, yend = mu_comp), linetype = 'dashed', color='blue') +
geom_segment(aes(x = 0, xend = 2500, y = mu_pangloss, yend = mu_pangloss), linetype = 'dashed', color='blue') +
geom_segment(aes(x = 983, xend = 983, y = 0, yend = values[984,3]), color='red') +
labs(x = "Nb. sinistres", y = "Prime") +
ylim(0, 20)+
theme_bw()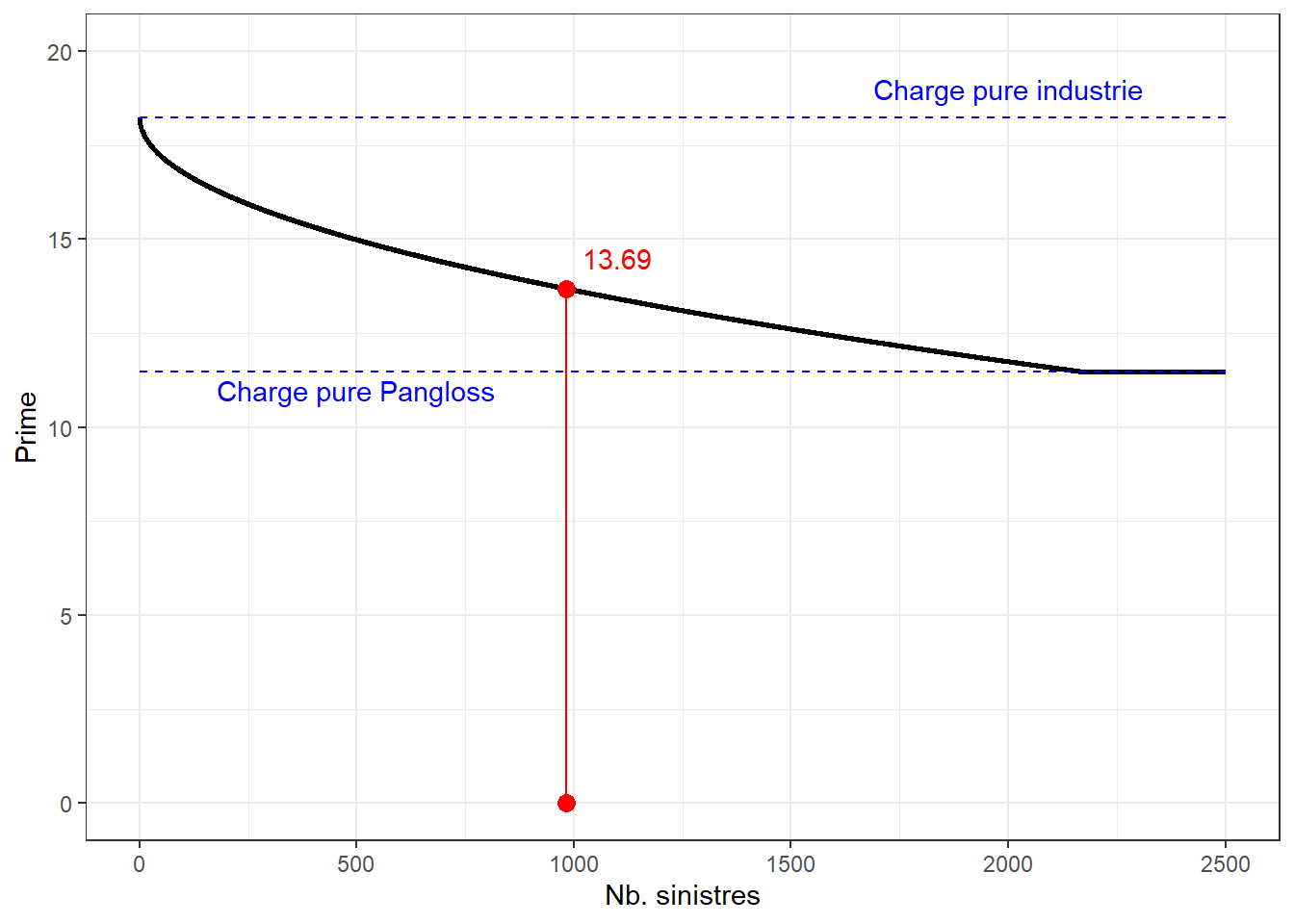
Exemple 3.9 Dans un modèle Poisson composé, \(E[N] = 725\), \(S_i \sim Gamma(100,000; 20)\) et la charge pure pour la population totale est de 105$ par unité d’exposition. Si la charge pure observée de la dernière année a été de 90$, calculez la prime de crédibilité d’ordre \((K =0.05; p=0.95)\) pour l’année suivante.