5.3 Sévérité des réclamations

Au lieu de modéliser la fréquence de réclamations, on pourrait aussi analyser la sévérité des réclamations avec lmodèle exponentiel-gamma, par exemple.

On prend encore le jeu de données dbfictif.Rda. Nous nous intéressons maintenant à la sévérité des réclamations. Cela signifie que nous ne considérons pas les assurés qui n’ont pas réclamés.

db <- db.fictif %>%
  filter(nb.sin > 0)

nrow(db)

## [1] 63493

sum(db$nb.sin)

## [1] 73703

Le jeu de données db contient $63,493$ observations, pour un total de $73,703$ sinistres. En effet, certains assurés ont plus d’une réclamation par contrat. Il nous faut donc modifier le jeu de données db pour qu’il y ait un sinistre par observation (pour avoir l’une des caractéristiques de ce qu’on appelait tidy data au premier chapitre).

La fonction gather du package tidyr crée une nouvelle observation pour chacune des colonnes Cost1 à Cost7. Pour ne pas créer d’observation lorsque les colonnes Cost2 à Cost7 sont nulles, un filtre est ajouté.

library(tidyr)
db <- db %>%
  gather(Rang, Cost, Cost1:Cost7) %>%
  filter(Cost > 0)

nrow(db)

## [1] 73703

Le jeu de données db contient maintenant $73,703$ observations, soit exactement le nombre de sinistres dans la base de données dbfictif.Rda originale.

Avant d’appliquer un modèle de crédibilité bayésienne, on peut analyser quelques éléments sommaires.

library(stats)
# moyenne
mean(db$Cost)

## [1] 6623.502

# variance
var(db$Cost)

## [1] 894671899

#variance comme puissance de la moyenne
log(var(db$Cost))/log(mean(db$Cost))

## [1] 2.3427

# quantiles
quantile(db$Cost, probs = seq(0, 1, 0.1),)

##          0%         10%         20%         30%         40%         50%         60%         70%         80%         90%        100% 
##      50.040     123.014     173.220     251.726     367.260     519.640     748.492    1122.904    2155.160   14875.598 1538270.040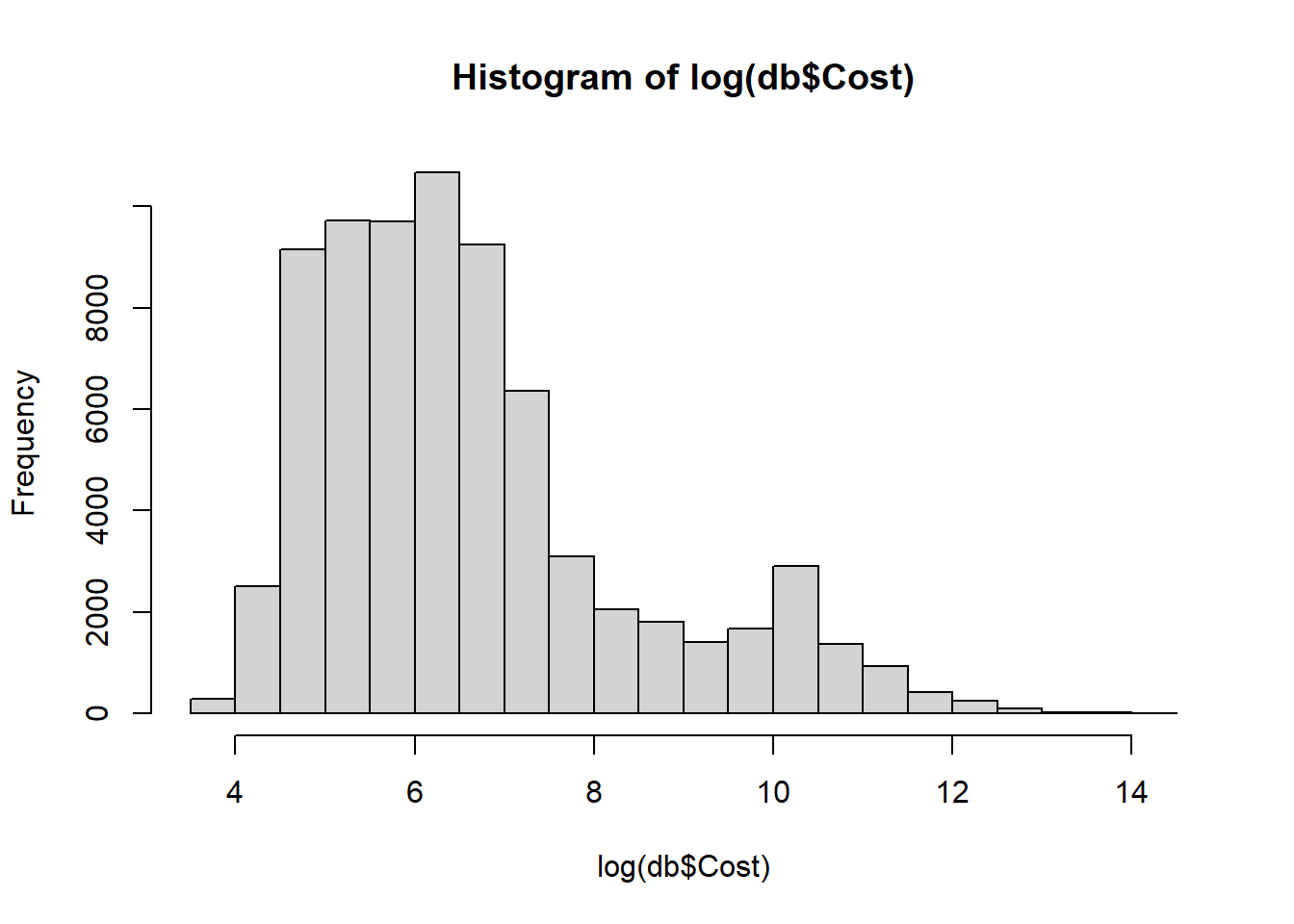

# histogramme du log(cost)
hist(log(db$Cost))

Tout comme on l’avait fait pour les réclamations, une première tarification simple serait d’assigner un coût moyen de $6623.502$ à toutes les réclamations. De cette manière, nous avons au minimum un équilibre financier.

db$prime.sev <- mean(db$Cost)

c(sum(db$prime.sev), sum(db$Cost))

## [1] 488171982 488171982

Il pourrait être intéressant de voir si la sévérité passée donne de l’information sur la modélisation de la sévérité future.

db2 <- db %>%
  arrange(policy_no, veh.num, Rang) %>%
  group_by(policy_no, veh.num) %>%
  mutate(claim.no = row_number(),
         past.cost = cumsum(Cost)- Cost, 
         mean.past = ifelse(claim.no >0, past.cost/(claim.no - 1), NA)) %>%
  ungroup()

claim1 <- db2 %>%
  filter(claim.no == 1) %>%
  summarize(sev0 = mean(Cost))

db2 <- db2 %>%
  filter(claim.no > 1) %>%
  dplyr::select(mean.past, Cost) %>%
  mutate(past_group = floor(mean.past/500) * 500) %>%
  group_by(past_group) %>%
  summarise(mean.sev = mean(Cost),
            n_claim = n())

ggplot(db2, aes(x = past_group, y = mean.sev, size = n_claim)) +
  geom_point(show.legend = FALSE) +
  geom_hline(yintercept = claim1$sev0, color='red', linetype='dashed')+
  labs(y = "Sévérité", x = "Moyenne des réclamations passées") +
  xlim(0, 20000)+ ylim(0, 12000)+
  theme_bw()

## Warning: Removed 263 rows containing missing values (`geom_point()`).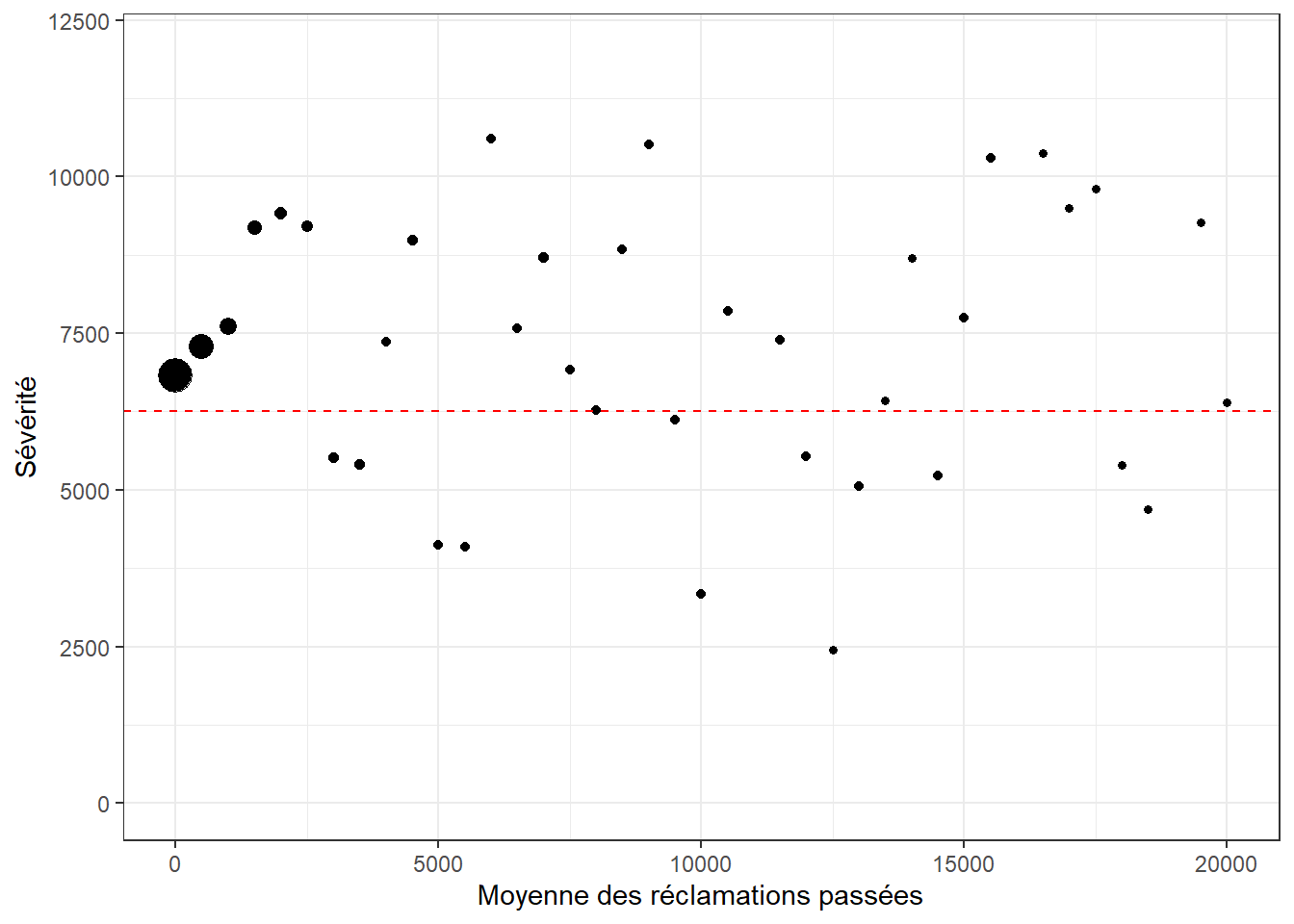

La ligne rouge représente la sévérité moyenne de premier sinistre, c’est-à-dire une réclamation n’ayant aucun sinistre passé. Les points noirs du graph représentent, quant à eux, la moyenne de la sévérité en fonction de la moyenne de réclamations passées. Des pas de 500$ ont été utilisés pour discrétiser la moyenne des réclamations passées.

Les résultats des données sont peu concluants. Pour les petites réclamations, les 6 premiers points pour moins de 3000$, on semble voir que la sévérité moyenne augmente en fonction de la moyenne des réclamations. Ces trois points qui sont assez gros et qui composent ainsi une proportion importante des sinistres, sont supérieurs à la ligne rouge. Si cette tendant était restée pour les autres points, on aurait pu proposer que le coût des réclamations passées donne une indication de la sévérité future. Par contre, pour une moyenne de réclamations supérieure à 3000$, aucune tendance claire n’est visible.

Utiliser des modèles de crédibilité pour modéliser la sévérité des réclamations est souvent difficile car le montant des sinistres passés n’est pas souvent un bon indicateur du coût des sinistres futurs. C’est pourquoi la tarification par expérience se base habituellement sur le nombre de réclamations passées, et non sur les coûts.

Ceci génère des situations où l’augmentation de prime produite après la réclamation d’un sinistre pourrait être plus élevée que le coût de la réclamation. Dans un tel cas, qu’on appelle soif du bonus il est peu stratégique pour l’assuré de réclamer ce sinistre.