4.1 Introduction

Tel qu’en témoigne le titre de ce chapitre, nous utiliserons la théorie bayésienne pour calculer une prime crédibilisée. Nous utiliserons aussi le terme de prime prédictive, ce qui correspond à la tarification d’un assuré en fonction de son historique de sinistres.

Au chapitre précédent, on parlait de crédibilité de stabilité. On réfère souvent à la crédibilité bayésienne en parlant de crédibilité de précision.

4.1.1 Exemple des deux urnes

Exemple 4.1 On suppose 2 urnes \(A\) et \(B\). L’urne A contient \(10\) balles numérotées de \(1\) à \(10\), et l’urne B contient \(5\) balles numérotées de \(1\) à \(5\). On sélectionne une urne au hasard, dans laquelle nous effectuons plusieurs tirages consécutifs avec remise. On note \(U\), la variable aléatoire représentant l’urne pigée et, \(T_i\) le résultat du \(i^e\) tirage.

Calculez la valeur espérée d’un premier tirage si nous connaissons l’urne pigée;
Calculez la valeur espérée d’un premier tirage si nous ne connaissons pas l’urne pigée;
Lors du premier tirage, nous pigeons une balle dont le numéro est \(3\). Déterminez la probabilité que la bille pigée provienne de l’urne A, ou encore de l’urne B;
Déterminez la valeur espérée du deuxième tirage, sachant que nous ne connaissons pas l’urne choisie et que nous avons pigé une balle dont le numéro était \(3\) lors du premier tirage.

(Exemple à faire en classe)

Quelques remarques importantes suite à ce premier exemple:

Lorsque nous ne connaissons pas l’urne pigée pour les tirages, tous les tirages sont dépendants;
Lorsque nous connaissons l’urne pigée pour les tirages, tous les tirages sont indépendants. On dit que les tirages sont conditionnellement indépendants;
Il s’agit d’un exemple classique pour expliquer la différence entre une contagion apparente et une vraie contation:

Le fait d’avoir obtenu une bille numérotée \(3\) au premier tirage ne modifie pas la manière dont seront effectués les prochains tirages, mais nous donne meilleure une idée de l’identité de l’urne pigée. Ainsi, alors que nous avions \(50\%\) d’avoir pigée l’urne \(A\) au début de l’expérience, nous passons à une probabilité de \(33.3\%\) lorsque nous savons que le premier tirage est une bille numérotée \(3\).

Une illustration de vraie contagion serait de modifier la composition des urnes en fonction des tirages passés, par exemple, ajouter de nouvelles billes en fonction de la bille pigée.

En 3e année du baccalauréat en actuariat, l’exemple précédent peut sembler trop simple. Pourtant, il capture pratiquement tous les éléments importants de la théorie de la crédibilité bayésienne.

Dans votre étude pour le cours, si tout semble devenir trop complexe, particulièrement la notation et les définitions, je recommande de refaire cet exemple plusieurs fois pour mieux comprendre la formalisation mathématique que nous verrons plus tard.

4.1.2 Exemple des deux types de conducteurs

Exemple 4.2 Les études en sécurité routière sont claires: le risque d’avoir un accident est fortement augmenté lorsque le conducteur utilise son téléphone en conduisant.

Malheureusement, lorsque les agents d’assurance posent la questions, les assurés n’avouent pas être des texteurs. Nous avons toutefois les statistiques suivantes:

Il existe 2 types de conducteurs \(C\) au sein de la population: une proportion \(p_b\) de bons conducteurs qui ne textent pas au volant, et une proportion \(p_m\) de mauvais conducteurs qui textes. On aurait pu aussi les appeler les texteurs et les non-texteurs;
On ne sait pas à quel type de conducteurs \(C\) appartient chaque assuré;
Le nombre de sinistres réclamés par un assuré pour l’année \(t\), \(N_{t}\), suit une loi de Poisson de moyenne \(\lambda_b\) pour les bons conducteurs et de moyenne \(\lambda_m\) pour les mauvais conducteurs;
Lorsque nous connaissons le type de conducteur (texteurs ou non-texteurs), le nombre de sinistres réclamés à une certaine année est indépendant du nombre de sinistres réclamés à une autre année.

Pour un assuré quelconque, calculez:

\(E[N_t|C=b]\) et \(E[N_t|C=m]\), l’espérance du nombre de réclamations à l’année \(t\) lorsque nous connaissons le type du conducteur;
\(E[N_t]\), l’espérance du nombre de réclamation à l’année \(t\) lorsque nous ne connaissons pas le type du conducteur;
Déterminez la probabilité que \(C=b\), si le conducteur a réclamé \(k\) sinistres au cours de l’année \(t=1\);
\(E[N_2|N_1 = k]\), l’espérance du nombre de réclamation à l’année \(t=2\), sachant que l’assuré a réclamé \(k\) sinistres au cours de l’année \(t=1\).

(Exemple à faire en classe)

L’analogie entre ce dernier exemple et celui des urnes est direct. On peut néanmoins commencer à reconnaître l’idée d’une certaine forme de tarification puisque:

\(E[N_1]\) pourrait représenter la prime de la composante fréquence pour un nouvel assuré (appelée prime a priori );
\(E[N_2|N_1=k]\) pourrait représenter la prime de la composante fréquence d’un assuré lors de son renouvellement, sachant qu’il a réclamé \(k\) fois lors de son premier contrat (appelée prime prédictive).

L’exemple est plutôt général avec des valeurs de \(p_b, p_m, \lambda_b\) et \(\lambda_m\). Voyons ce que tout cela implique avec des valeurs numériques.

## initialisation des parametres ##
p_b <- 0.6
p_m <- 1 - p_b
lambda_b <- 0.10
lambda_m <- 0.50

## Calcul de primes a priori ##
(prime_apriori <- p_b*lambda_b + p_m*lambda_m)

## [1] 0.26

## Calcul de primes predictives ##
all.prime <- data.frame()
for(k in 0:10){
    num.bayes_b <- dpois(k, lambda = lambda_b) * p_b
    num.bayes_m <- dpois(k, lambda = lambda_m) * p_m
    pr.bayes_b <- num.bayes_b/(num.bayes_b+num.bayes_m)
    pr.bayes_m <- 1 - pr.bayes_b
    prime_pred <-  pr.bayes_b*lambda_b + pr.bayes_m*lambda_m
    pct <- 100*prime_pred/prime_apriori - 100
    all.prime <- rbind(all.prime, 
    c(k, 100*pr.bayes_b, 100*pr.bayes_m, prime_pred, pct))
}
colnames(all.prime) <- c("k", "pb", "pm", "Prime", "Pct")
all.prime %>% mutate_at(vars(pb, pm, Prime, Pct), ~ round(., 3))

##     k     pb      pm Prime     Pct
## 1   0 69.114  30.886 0.224 -14.022
## 2   1 30.918  69.082 0.376  44.742
## 3   2  8.216  91.784 0.467  79.668
## 4   3  1.759  98.241 0.493  89.602
## 5   4  0.357  99.643 0.499  91.759
## 6   5  0.072  99.928 0.500  92.198
## 7   6  0.014  99.986 0.500  92.286
## 8   7  0.003  99.997 0.500  92.303
## 9   8  0.001  99.999 0.500  92.307
## 10  9  0.000 100.000 0.500  92.308
## 11 10  0.000 100.000 0.500  92.308

Pour les valeurs choisies dans l’application informatique, on voit que la probabilité que l’assuré soit un bon conducteur approche zéro rapidement lorsque \(k\) augmente, ce qui fait que la prime tend vers \(0.50\), le nombre de réclamations attendues d’un mauvais conducteur.
Peu importe le nombre de réclamations \(k\), la prime prédictive de cet exemple sera toujours entre \(0.10\) et \(0.50\).
La diminution de prime est lente: la seule manière d’avoir une diminution de prime est de ne pas réclamer. Dans un tel cas, la prime passe de \(0.26\) à \(0.224\). À l’inverse, l’augmentation de prime peut être rapide si l’assuré réclame beaucoup.

Exemple 4.3 En suite de l’exemple précédent, calculez: \[E[N_{11}|N_1=n_1, N_2=n_2, \ldots, N_{10} =n_{10}].\]

(Exemple à faire en classe)

On voit que l’espérance prédictive pour la \(T+1^e\) année, que l’on note \(E[N_{T+1}|N_1=n_1, N_2=n_2, \ldots, N_{T} =n_{T}]\), dépend uniquement de:

1- La valeur de \(T\);

2- La somme des réclamations des \(T\) dernières années, \(\sum_{t=1}^{T} n_t\).

Cela signifie que la répartition de ces réclamations à travers les \(T\) dernières années ne changent aucunement l’espérance prédictive. Un assuré réclamant une fois tous les ans, pendant \(T\) années, aura la même prime prédictive qu’un assuré ayant réclamé la totalité de ses \(T\) réclamations pendant la même année.

Application des résultats à l’aide de R.

## historique de 10 ans ###
all.prime <- data.frame()
for(sum.n in 0:15){
    num.bayes_b <- exp(-10*lambda_b) * lambda_b^sum.n * p_b
    num.bayes_m <- exp(-10*lambda_m) * lambda_m^sum.n * p_m
    pr.bayes_b <- num.bayes_b/(num.bayes_b+num.bayes_m)
    pr.bayes_m <- 1 - pr.bayes_b
    prime_pred <-  pr.bayes_b*lambda_b + pr.bayes_m*lambda_m
    all.prime <- rbind(all.prime, 
    c(sum.n, 100*pr.bayes_b, 100*pr.bayes_m, prime_pred))
}
colnames(all.prime) <- c("sum.n", "pb", "pm", "Prime")
all.prime %>% mutate_at(vars(pb, pm, Prime), ~ round(., 3))

##    sum.n     pb      pm Prime
## 1      0 98.794   1.206 0.105
## 2      1 94.246   5.754 0.123
## 3      2 76.613  23.387 0.194
## 4      3 39.584  60.416 0.342
## 5      4 11.585  88.415 0.454
## 6      5  2.554  97.446 0.490
## 7      6  0.521  99.479 0.498
## 8      7  0.105  99.895 0.500
## 9      8  0.021  99.979 0.500
## 10     9  0.004  99.996 0.500
## 11    10  0.001  99.999 0.500
## 12    11  0.000 100.000 0.500
## 13    12  0.000 100.000 0.500
## 14    13  0.000 100.000 0.500
## 15    14  0.000 100.000 0.500
## 16    15  0.000 100.000 0.500

Pour une valeur de \(T\) fixée à 10, la seule variable qui peut modifier la prime est \(\sum_{t=1}^{T} n_t\);
Contrairement à la crédibilité de stabilité, on voit que la prime d’un assuré peut changer après une seule année d’expérience;
Un assuré avec 2 réclamations ou moins au cours des 10 dernières années a une prime plus basse que la prime a priori (\(0.26\));
La probabilité qu’un assuré ayant 10 réclamations au cours des 10 dernières soit un mauvais conducteur est de \(99.999\%\);
La probabilité qu’un assuré n’ayant aucune réclamation au cours des 10 dernières soit un bon conducteur est de \(98.794\%\).

En modifiant légèrement le code informatique plus haut, il est aussi possible de calculer la prime d’un assuré selon la longueur de son historique de sinistres. Les graphiques ci-dessous présentent l’évolution de la prime en fonction du nombre de sinistres, pour un historique de 10 ans, de 100 ans et de 500 ans.

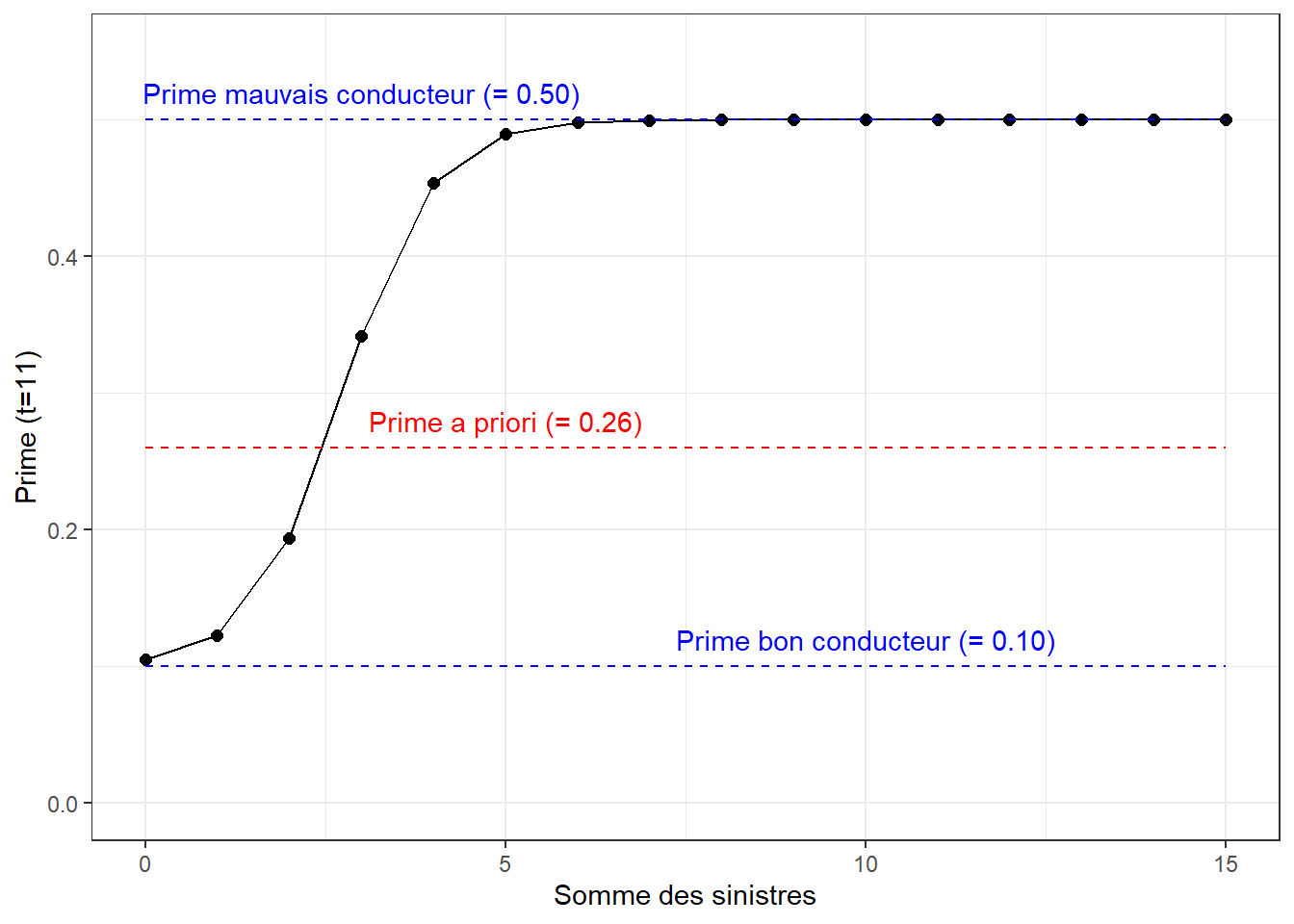
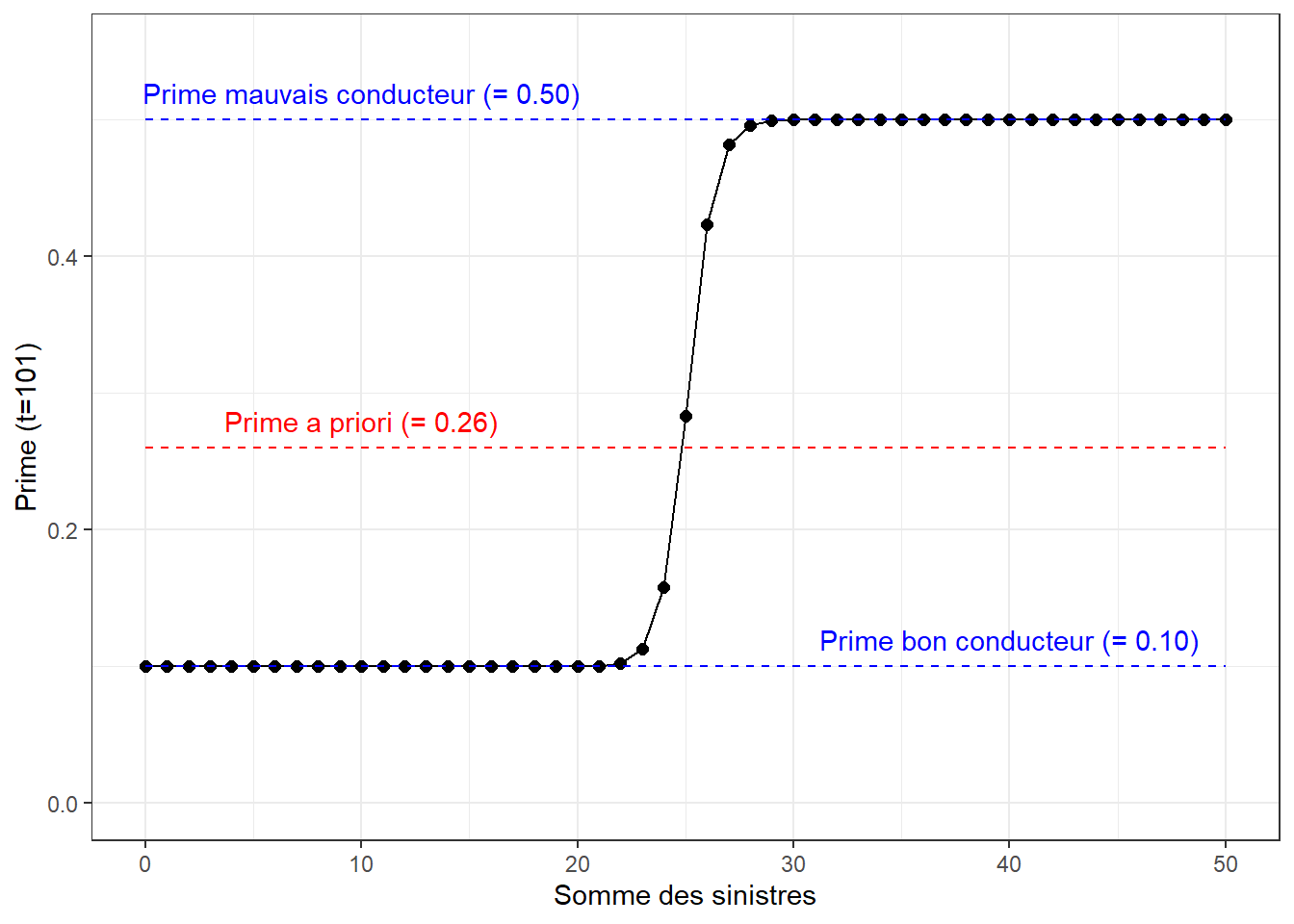
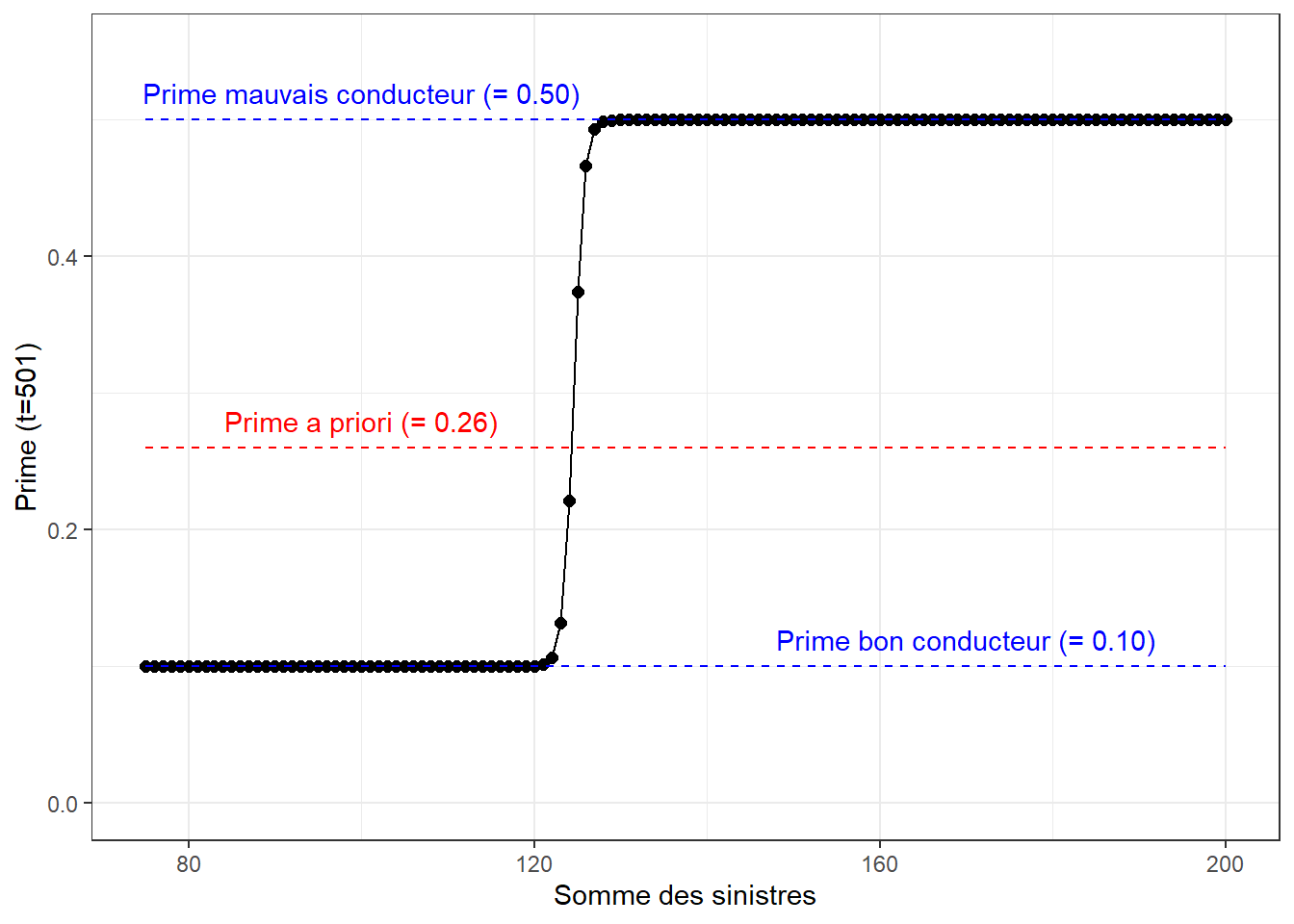
On y voit qu’il devient de plus en plus facile d’identifier le profil du conducteur (bon ou mauvais) en augmentant l’historique de réclamations.