5.2 Fréquence de réclamations
Pour pouvoir appliquer les modèles bayésiens, on ne prend que les polices qui contiennent des contrats annuels ayant une exposition au risque plus grande 0.8.
`%notin%` <- Negate(`%in%`)
remove <- db.fictif[which(db.fictif$expo < 0.8),]
data <- db.fictif[which(db.fictif$policy_no %notin% unique(remove$policy_no)),]Avant d’appliquer certains modèles bayésiens, il pourrait être intéressant de faire une analyse sommaire de la fréquence de réclamation.
c(mean(data$nb.sin), var(data$nb.sin), var(data$nb.sin)/mean(data$nb.sin), min(data$nb.sin), max(data$nb.sin))## [1] 0.1860964 0.2113058 1.1354641 0.0000000 7.0000000On peut aussi analyser la distribution du nombre de sinistres.
##
## Attaching package: 'janitor'## The following objects are masked from 'package:stats':
##
## chisq.test, fisher.test## nb.sin n percent
## 0 144067 0.839923276043
## 1 23577 0.137455982836
## 2 3368 0.019635736107
## 3 451 0.002629369651
## 4 55 0.000320654835
## 5 3 0.000017490264
## 6 2 0.000011660176
## 7 1 0.000005830088
## Total 171524 1.000000000000Pour mettre en place le modèle de crédibilité bayésienne, on pourrait débuter par analyser le comportement de chaque véhicule en fonction de son historique de réclamations. Analysons la fréquence de réclamations et regardons le nombre de réclamations moyen:
## [1] 0.1860964Ainsi, pour la portion fréquence de la prime, on pourrait charger \(0.1860964\) par année à tous les assurés. On aurait ainsi un équilibre financier car la somme des primes serait égale à la somme des sinistres.
## [1] 31920 31920Maintenant, on pourrait voir si une prime unique à tous les assurés, peu importe leur historique de réclamations, est juste.
data <- data %>%
arrange(policy_no, veh.num, renewal_date) %>%
group_by(policy_no, veh.num) %>%
mutate(contract.no = row_number(),
past.nbclaim = cumsum(nb.sin)- nb.sin) %>%
ungroup()Le code précédent fait les calculs suivants:
Avec la fonction arrange(), il trie le jeu de données selon policy_no, veh.num et renewal_date;
Avec la fonction group(), il groupe toutes les observations ayant les mêmes valeurs de policy_no, veh.num;
De cette manière, en utilisant le numéro de la ligne, row_number(), on peut déterminer si un véhicule a plus d’un contrat dans la base de données. Plus précisément, on compte le rang de chaque contrat.
Avec la fonction cumsum(), on compte le nombre de sinistres cumulatif pour chaque véhicule (ou soustrait nb.sin afin de n’avoir que le nombre de sinistres passés)
Pour mieux voir le calcul précédent, on peut sélectionner un véhicule précis.
data %>%
filter(policy_no==6007503 & veh.num == 1) %>%
select(policy_no, veh.num, renewal_date, nb.sin, contract.no, past.nbclaim)## # A tibble: 8 × 6
## policy_no veh.num renewal_date nb.sin contract.no past.nbclaim
## <dbl> <int> <date> <int> <int> <int>
## 1 6007503 1 2012-01-03 0 1 0
## 2 6007503 1 2013-01-03 0 2 0
## 3 6007503 1 2014-01-03 0 3 0
## 4 6007503 1 2015-01-03 1 4 0
## 5 6007503 1 2016-01-03 0 5 1
## 6 6007503 1 2017-01-03 0 6 1
## 7 6007503 1 2018-01-03 1 7 1
## 8 6007503 1 2019-01-03 0 8 2On voit ainsi que dans notre jeu de données, le véhicule 2 de la police 6007503 a 8 contrats annuels (se renouvellant à chaque 3 janvier). Un sinistre a été réclamé lors du contrat 4 et du contrat 7. Ainsi, en comptant le nombre de sinistres passés, les contrats 5, 6 et 7 indiquent past.nbclaim == 1, alors que le contrat 8 indique past.nbclaim == 2.
En ayant contrat.no et past.nbclaim, on peut donc vérifier si le nombre de réclamations moyen dépend du nombre de réclamations passées, et si une prime de \(0.1860964\) par année à tous les assurés semble équitable.
sommaire1 <- data %>%
mutate(past.nbclaim = pmin(4, past.nbclaim)) %>%
group_by(contract.no, past.nbclaim) %>%
summarise(nb = n(),
freq = mean(nb.sin), .groups = 'drop') %>%
mutate(pct = freq/0.1860964) %>%
filter(contract.no < 5) %>%
ungroup()Au lieu d’analyser un tableau de chiffres, on peut simplement illustrer le résultat en utilisant une heatmap.
ggplot(sommaire1, aes(as.factor(contract.no), as.factor(past.nbclaim), fill= as.numeric(pct))) +
geom_tile()+
geom_text(aes(label = paste(sprintf("%0.1f", 100*pct),'% (', sprintf("%0.0f", nb), ')') ), color = "black", size = 4) +
scale_fill_gradient2(low = "green", mid = "gray", midpoint = 1, high = "red")+
xlab("No. contrat") + ylab("Nb. réclamations passées")+
theme(legend.position = 'none')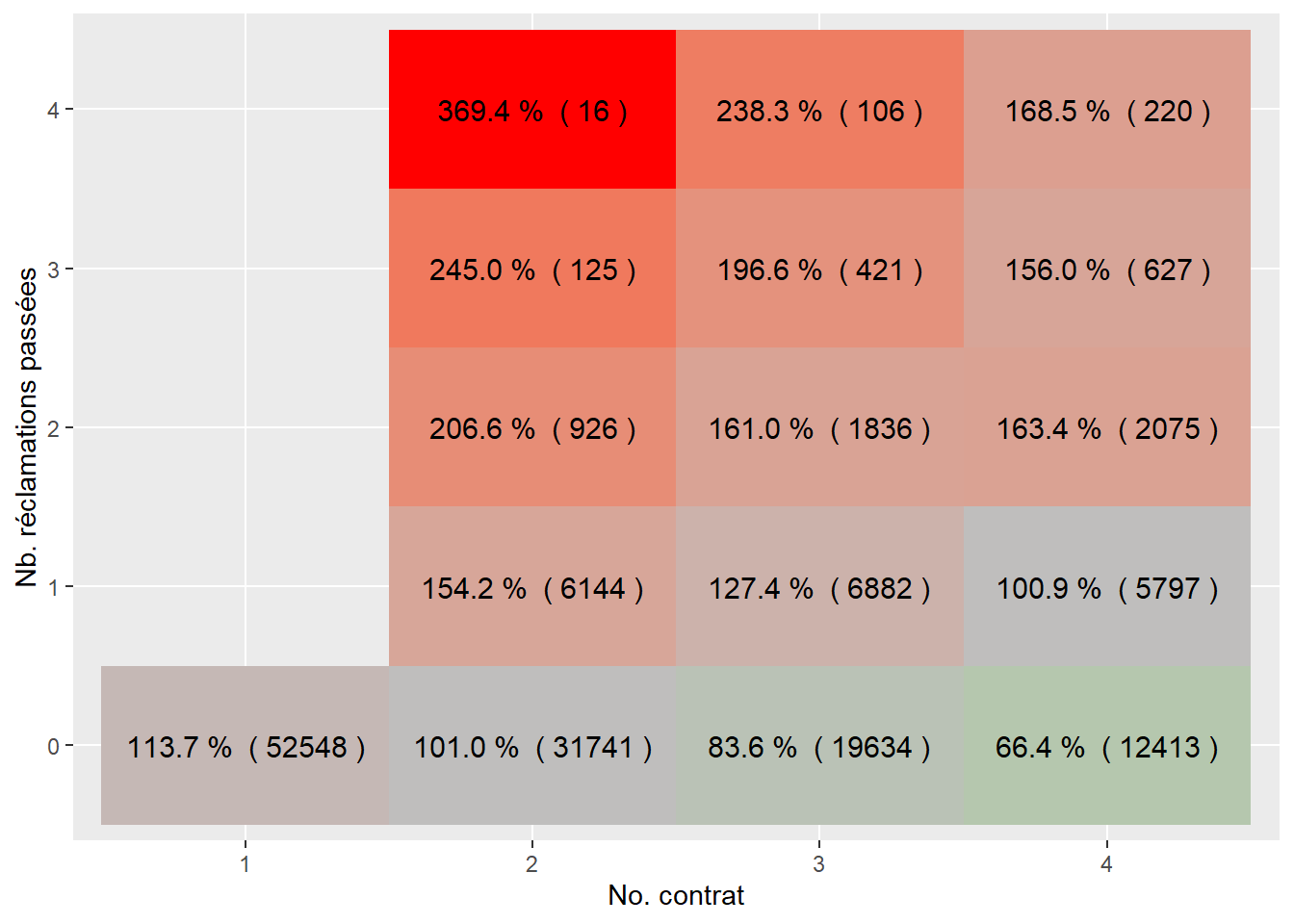
Il faut bien entendu remarquer que l’exposition totale pour chaque tuile n’est pas la même (chiffre entre parenthèses), et que la majorité des assurés ne réclament pas. Par contre, on peut voir certaines tendances assez nettes:
- les assurés réclamant dans le passé ont une fréquence de réclamations supérieure à la prime moyenne;
- les assurés qui ne réclament pas semblent ont une fréquence de réclamations inférieure à la prime moyenne;
- les nouveaux assurés, c’est-à-dire ceux qui n’ont aucune expérience d’assurance, ont une fréquence de réclamations supérieure à la moyenne.
5.2.1 Modèle Poisson-gamma
Comme on l’a vu précédemment, on pourrait donc appliquer un modèle de crédibilité bayésienne afin d’augmenter la prime des assurés qui réclament, et diminuer la prime des assurés qui ne réclament pas.
Supposons ainsi \(S_t|\Theta = \theta \sim Poisson(\theta)\), et \(\Theta \sim gamma(\alpha, \tau)\), qui semble un modèle idéal dans notre cas. Au chapitre précédent, nous avons vu que:
1- La prime a priori d’un assuré est égale à \(\frac{\alpha}{\tau}\);
2- La prime prédictive d’un assuré est égale à \(\frac{\alpha + s_{\bullet}}{\tau + T}\).
Le problème pratique des modèles bayésiens est dans l’estimation des paramètres. Il n’est en effet pas si simple ni direct d’estimer adéquatement les paramètres \(\alpha\) et \(\tau\) pour le modèle Poisson-gamma. La procédure d’estimation de ce type de modèles nécessiterait un cours sur les données longitudinales, ce qui dépasse totalement les objectifs du cours.
Pour poursuivre l’illustration et voir l’utilité de la crédibilité bayésienne en pratique, je vous donne toutefois les valeurs estimées de ces paramètres, soit \(\hat{\alpha} = 1.73778\) et \(\hat{\tau} = 9.182881\).
data <- data %>%
mutate(alpha = 1.73778,
tau = 9.182881,
prime.pg = (alpha + past.nbclaim)/(tau + (contract.no-1)))
c(sum(data$prime.pg), sum(data$nb.sin))## [1] 32633.84 31920.00Sur la totalité du portefeuille, nous n’avons plus un équilibre financier puisque la somme des sinistres n’est plus égale à la somme des primes.
On peut analyser la prime générée en fonction de l’historique de sinistre
sommaire2 <- data %>%
group_by(contract.no, past.nbclaim) %>%
summarise(nb = n(),
freq = mean(nb.sin),
prime = mean(prime.pg),
.groups = 'drop') %>%
mutate(pct = freq/prime) %>%
filter(contract.no < 5) %>%
ungroup()
ggplot(sommaire2, aes(as.factor(contract.no), as.factor(past.nbclaim), fill= as.numeric(prime))) +
geom_tile()+
geom_text(aes(label = paste(sprintf("%0.3f", prime), '(', sprintf("%0.0f", nb), ')') ), color = "black", size = 4) +
scale_fill_gradient2(low = "green", high = "red")+
xlab("No. contrat") + ylab("Nb. réclamations passées")+
theme(legend.position = 'none')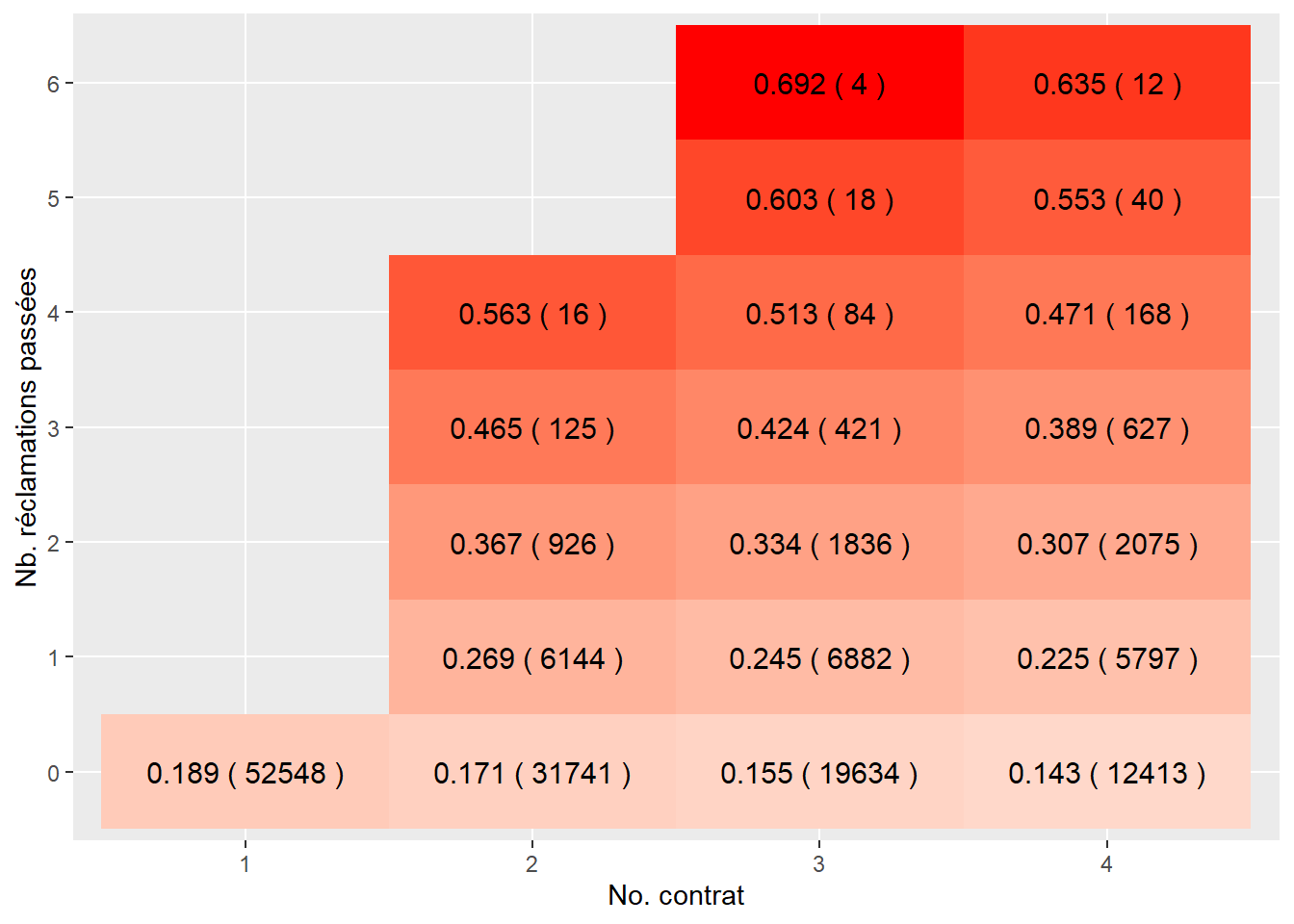
On peut aussi comparer l’expérience de réclamation avec la prime calculée.
sommaire3 <- sommaire2 %>% filter(past.nbclaim <= 4)
ggplot(sommaire3, aes(as.factor(contract.no), as.factor(past.nbclaim), fill= as.numeric(pct))) +
geom_tile()+
geom_text(aes(label = paste(sprintf("%0.1f", 100*pct),'% (', sprintf("%0.0f", nb), ')') ), color = "black", size = 4) +
scale_fill_gradient2(low = "green", mid = "gray", midpoint = 1, high = "red")+
xlab("No. contrat") + ylab("Nb. réclamations passées")+
theme(legend.position = 'none')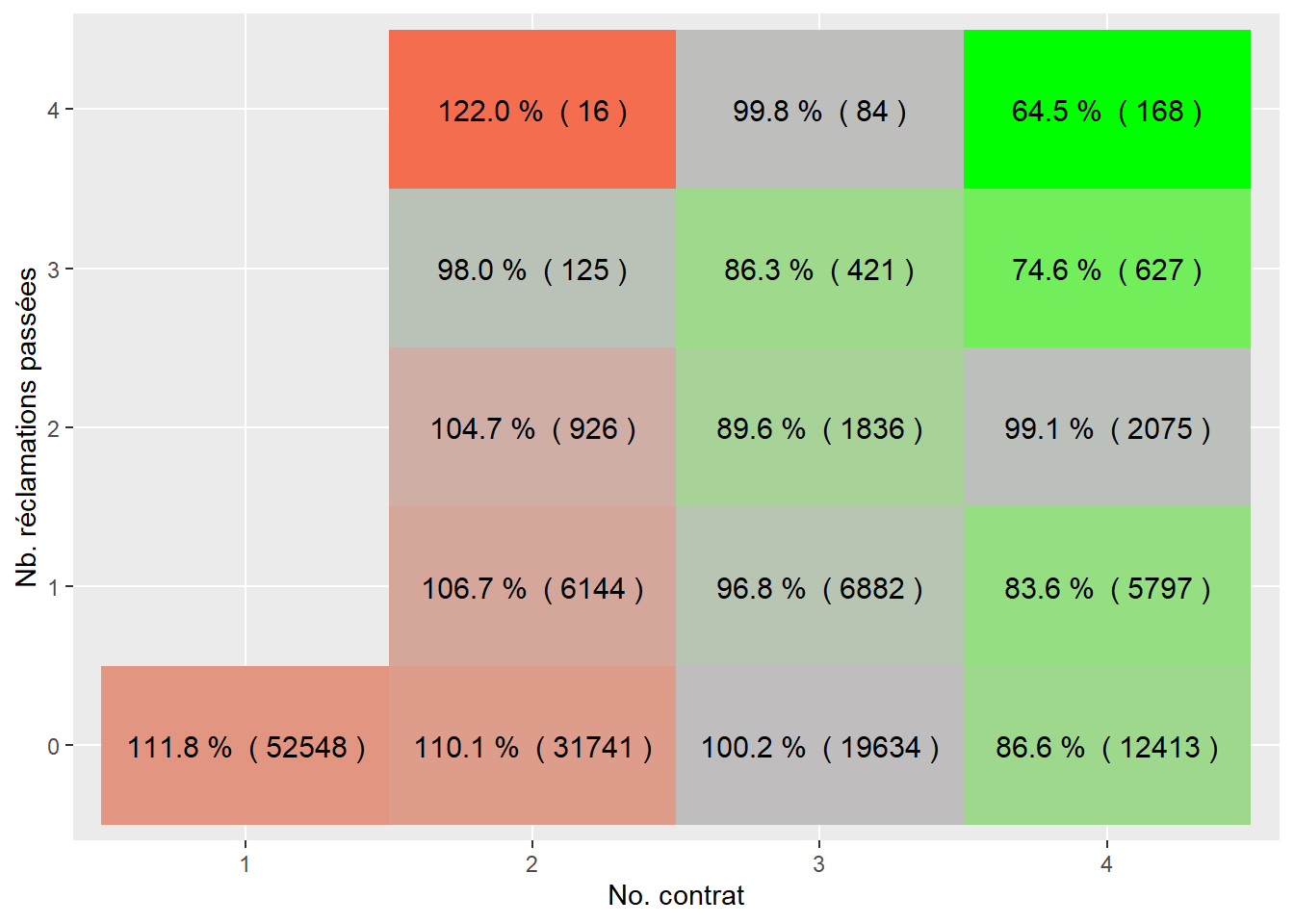
Ce n’est pas encore parfait, mais le modèle de prime prédictive bayésien est beaucoup plus équitable qu’une tarification qui ne tiendrait pas compte des réclamations passées.