4.4 Poisson-gamma

Supposons ainsi que nous avons \(S_t|\Theta = \theta \sim Poisson(\theta)\), avec \(\Theta \sim gamma(\alpha, \tau)\). Nous aurions ainsi la fonction de probabilité et la fonction de densité suivante:

\[ \underbrace{\Pr[S_t=s_t|\Theta=\theta] = \frac{\theta^{s_t} e^{-\theta}}{s_t!}}_{\text{Distribution conditionnelle}} \text{ pour } s_t \in \mathbb{N}\]

\[ \underbrace{f(\theta) = \frac{\tau^{\alpha}}{\Gamma(\alpha)} \theta^{\alpha - 1} e^{-\tau \theta}}_{\text{Distribution a priori}}, \text{ pour } \theta > 0, \text{ et } \alpha > 0, \tau >0.\]

---

Exercice 4.3 Trouvez les distributions suivantes:

1. La distribution marginale de \(S_{t}\);
2. La distribution a posteriori de \(\Theta\), sachant \(S_{1}=s_{1}, \ldots,S_{T}=s_{T}\);
3. La distribution prédictive de \(S_{T+1}\), sachant \(S_{1}=s_{1}, \ldots ,S_{T}=s_{T}\).

(Exercice à faire en classe)

---

Exercice 4.4 Trouvez les primes suivantes:

1. La prime de risque;
2. La prime collective;
3. La prime prédictive au temps \(t=T\);
4. La prime chargée à un nouvel assuré;
5. Le coefficient de crédibilité \(\mathsf{Z}\) pour la prime de crédibilité.

(Exercice à faire en classe)

---

Définition 4.1 (Distribution conjuguée) Une fonction de densité a priori \(g_{\Theta}(\theta)\) est dite conjuguée à la distribution conditionnelle (\(f_S(s|\theta)\)) si la densité a posteriori correspondante (notée \(g_{\Theta}(\theta|s_1,...,s_T)\)) est de la même forme que la densité a priori. Par même forme, on veut signifier que les deux fonction de densités correspondent à la même distribution, où seuls les paramètres sont différents.

---

Les résultats obtenus par le modèle Poisson-gamma sont tout-à-fait extraordinaires et permettent plusieurs interprétation de la tarification par expérience. Mais au lieu de regarder toutes les équations obtenues pour ce modèle, il est plus simple de faire quelques exemples pratiques qui permettront de mieux expliquer le modèle.

---

Exemple 4.8 On suppose une structure de tarification basée sur le modèle \(N_T |\Theta = \theta \sim Poisson(\theta)\), avec \(\Theta \sim gamma(\alpha = 0.6, \tau = 4)\).

Déterminez les différentes primes du modèle, au temps \(t=1, \ldots, 7\), si un assuré a eu l’expérience de sinistres suivante:

Année	Nb. de sin.
1	0
2	1
3	0
4	4
5	0
6	1

Avant de faire les calculs, il faut bien réaliser qu’un assuré paye la prime en début d’année, et subit des sinistres pendant l’année.

(Réponse)

Nous reprenons la totalité des résultats précédents, alors aucun développement mathématique n’est nécessaire.

1. Prime de risque : \(\mu(\Theta) = \Theta\).

2. Prime collective et prime a priori: \(\frac{\alpha}{\tau} = \frac{0.6}{4} = 0.15\).

3. Prime bayésienne ou prime prédictive: \(\frac{\alpha + n_{\bullet}}{\tau + T} = \frac{0.6 + n_{\bullet}}{4 + T}\), avec \(n_{\bullet} = \sum_{t=1}^T n_t\);

4. Facteur de crédibilité \(\mathsf{Z} = \frac{T}{\tau + T} = \frac{T}{4 + T}\).

Au lieu de calculer chaque possibilité, passons directement en R.

---

an <- (1:7)
nbsin <- c(0,1,0,4,0,1,0)
df <- data.frame(an, nbsin)
alpha <- 0.6
tau <- 4

df %>%
  mutate(T=row_number() - 1,
         n.bullet = cumsum(nbsin)- nbsin,
         prime.coll = alpha/tau,
         prime.pred = (alpha + n.bullet)/(tau + T),
         Z = T/(tau+4),
         nbsin = ifelse(an==7, NA, nbsin))

##   an nbsin T n.bullet prime.coll prime.pred     Z
## 1  1     0 0        0       0.15  0.1500000 0.000
## 2  2     1 1        0       0.15  0.1200000 0.125
## 3  3     0 2        1       0.15  0.2666667 0.250
## 4  4     4 3        1       0.15  0.2285714 0.375
## 5  5     0 4        5       0.15  0.7000000 0.500
## 6  6     1 5        5       0.15  0.6222222 0.625
## 7  7    NA 6        6       0.15  0.6600000 0.750

---

Nous venons de voir que le facteur de crédibilité ne dépend que de \(T\) et de \(\tau\) car \(\mathsf{Z} = \frac{T}{\tau + T} = \frac{T}{4 + T}\). Cela signifie que la proportion de la prime qui dépend uniquement que de l’expérience individuelle d’un assuré peut être facilement analysée.

db <- expand.grid(c(0:20), seq(0.5, 4, by=0.5))
colnames(db) <- c('T', 'tau')
db$Z <- db$T/(db$tau + db$T)

ggplot() +
  geom_line(aes(x = T, y = Z, group=factor(tau), 
                color=factor(tau)), size=1, data=db)+
  labs(x = "T", y = "Facteur de credibilite (Z)", color="Tau")+
  ylim(0,1)+
  theme_bw()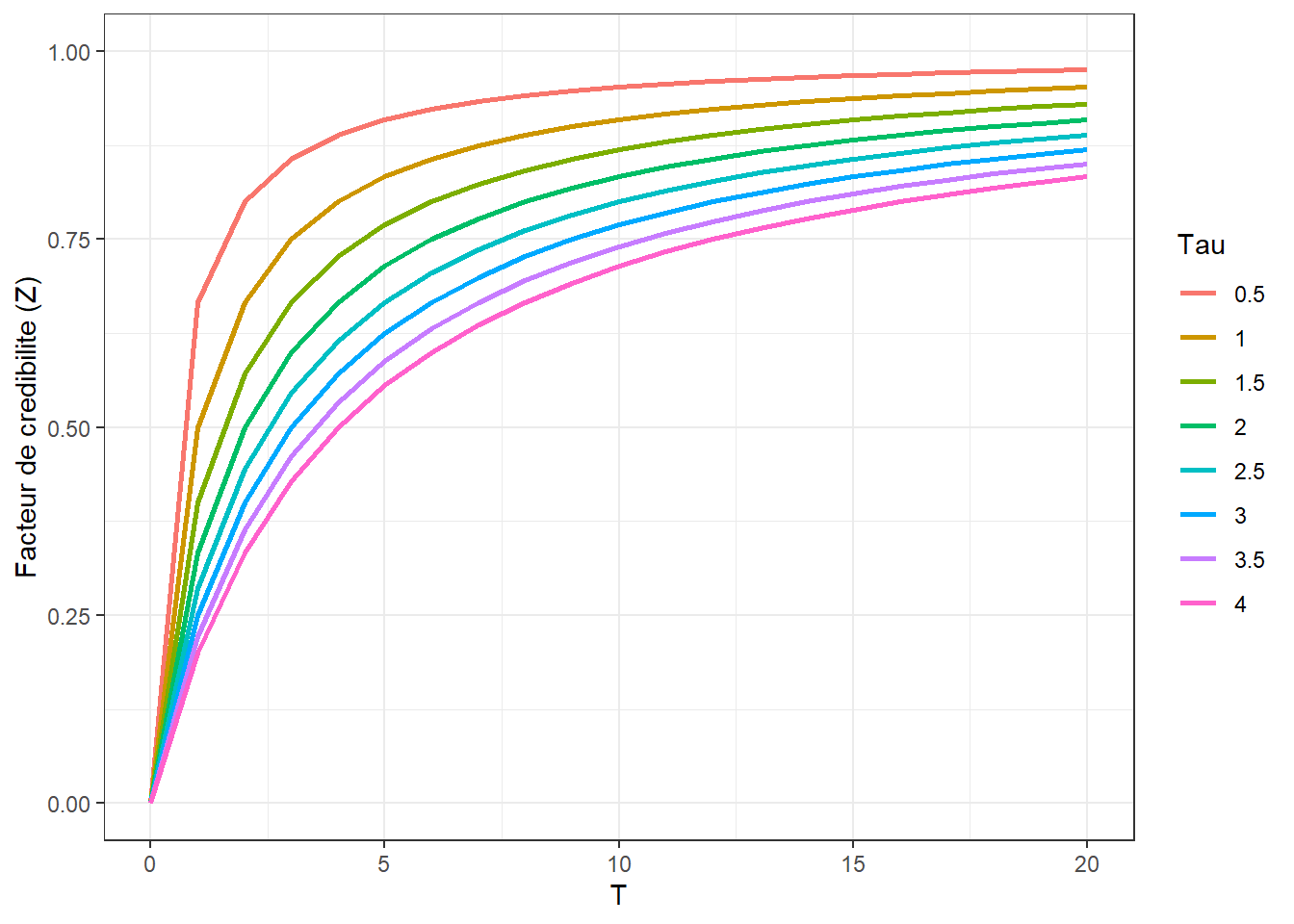    

---

Exemple 4.9 On suppose encore le modèle \(S_t|\Theta = \theta \sim Poisson(\theta)\), avec \(\Theta \sim Gamma(\alpha, \tau)\).

Calculez:

1. \(Var[S_t]\);

2. \(Var[S_{T+1}|S_1=s_1,S_2= s_2,...,S_{T}=s_{T}]\).

(Exemple à faire en classe)

---

Dernières remarques sur la Poisson-gamma

• Si on connait le paramètre de risque \(\Theta\) d’un assuré, tous ses contrats sont poissoniens et indépendants;

• Si on pige un assuré au hasard dans le portefeuille, sans connaître son paramètre de risque \(\Theta\), son nombre de réclamations annuelles suit une loi une binomiale négative, et les contrats d’un même assuré sont dépendants.

---