10.9 Optional: Tests for comparing the mean from two independent samples
(Answers available in Sect. A.10)
This question is optional; e.g., if you need more practice, or you are studying for the exam.
This question has a video solution in the online book, so you can hear and see the solution.
Batteries are expensive, so comparing the performance of expensive and cheap batteries is helpful.
A test on the lifetime of batteries (Lindström 2011) compared the time for two brands of \(1.5\) volt batteries to reduce their voltage to \(1.0\) volts under standard testing conditions.
The times (in hours) for nine Energizer Max batteries and nine ALDI brand batteries (Ultracell) are shown in Table 10.4.
| Energizer | 7.58 | 7.46 | 7.46 | 7.59 | 7.46 | 7.52 | 6.83 | 6.89 | 7.45 |
| Ultracell | 7.5 | 7.48 | 7.47 | 7.48 | 7.48 | 7.41 | 7.47 | 6.96 | 7.48 |
Write the hypotheses for testing the research question of interest. Is the test one- or two-tailed?
Explain the meaning of the standard error of the mean in this context.
The software output for the analysis is shown in Fig. 10.7 (jamovi) and Fig. 10.8 (SPSS). Determine the value of the \(t\)-statistic and the \(P\)-value for testing the hypotheses.
Write a statement that communicates the result of the test.
What conditions must be met for this test to be valid?
Is it reasonable to assume the assumptions are satisfied?
What did you learn from this study?
At the time of this analysis, a four-pack of the Ultracell Max batteries cost $2.49 from ALDI online, while a four pack of Energizer Max from Woolworths online cost $5.97 on special (usually $8.01)3.
On the basis of this information, would you be prepared to try the Ultracell batteries? Explain your reasoning.

FIGURE 10.7: Output from jamovi for the battery data
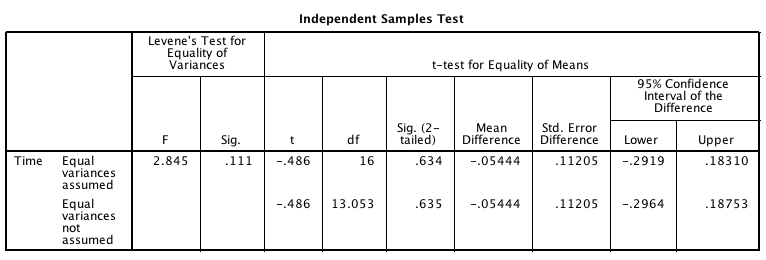
FIGURE 10.8: Output from SPSS for the battery data
References
Data from 05 September 2012.↩︎