9.10 Optional: Tests for paired samples
This question is optional; e.g., if you need more practice, or you are studying for the exam.
(Answers available in Sect. A.10)
This question has a video solution in the online book, so you can hear and see the solution.
After a number of runners collapsed near the finish of the Tyneside annual Great North Run, researchers decided to study the role of \(\beta\) endorphins as a factor in the collapses. (\(\beta\) endorphins are a peptide which suppress pain.)
A study (Dale et al. 1987) examined what happened with plasma \(\beta\) endorphins during fun runs: does the concentration of plasma \(\beta\) endorphins increase, on average, during fun runs.
The researchers recorded the plasma \(\beta\) concentrations in fun runners (participating in the Tyneside Great North Run). Eleven runners (who did not collapse) had their plasma \(\beta\) concentrations measured (in pmol/litre) before and after the race (Table 9.2.) A 'typical' value for \(\beta\) endorphines is usually under about 11 pmol/litre.
Explain why these data should be analysed as a paired means situation.
Which of the following is the correct null hypothesis for this question? Why are the others incorrect? Is the test one- or two-tailed?
- \(\mu_{\text{Before}} = \mu_{\text{After}}\)
- \(\mu_{\text{Difference}} = 0\)
- \(\mu_{\text{Before}} = 0\)
- \(\mu_{\text{After}} = 0\)
- \(\mu_{\text{Before}} < \mu_{\text{After}}\)
- \(\mu_{\text{Difference}} > 0\)
- \(\mu_{\text{Before}} < 0\)
- \(\mu_{\text{After}} > 0\)
Write down the mean, standard deviation and standard error, using Fig. 9.11 (jamovi) or Fig. 9.12 (SPSS).
Write down the value of the \(t\)-statistic, then estimate the \(P\)-value (using the \(68\)--\(95\)--\(99.7\) rule).
Write a statement that communicates the result of the test.
What conditions must be met for this test to be valid?
Is it reasonable to assume the assumptions are satisfied? Use the histogram of the data in Fig. 9.13 to help, if necessary.
| Before | After | Difference |
|---|---|---|
| 4.3 | 29.6 | 25.3 |
| 4.6 | 25.1 | 20.5 |
| 5.2 | 15.5 | 10.3 |
| 5.2 | 29.6 | 24.4 |
| 6.6 | 24.1 | 17.5 |
| 7.2 | 37.8 | 30.6 |
| 8.4 | 20.1 | 11.7 |
| 9.0 | 21.9 | 12.9 |
| 10.4 | 14.2 | 3.8 |
| 14.0 | 34.6 | 20.6 |
| 17.8 | 46.2 | 28.4 |
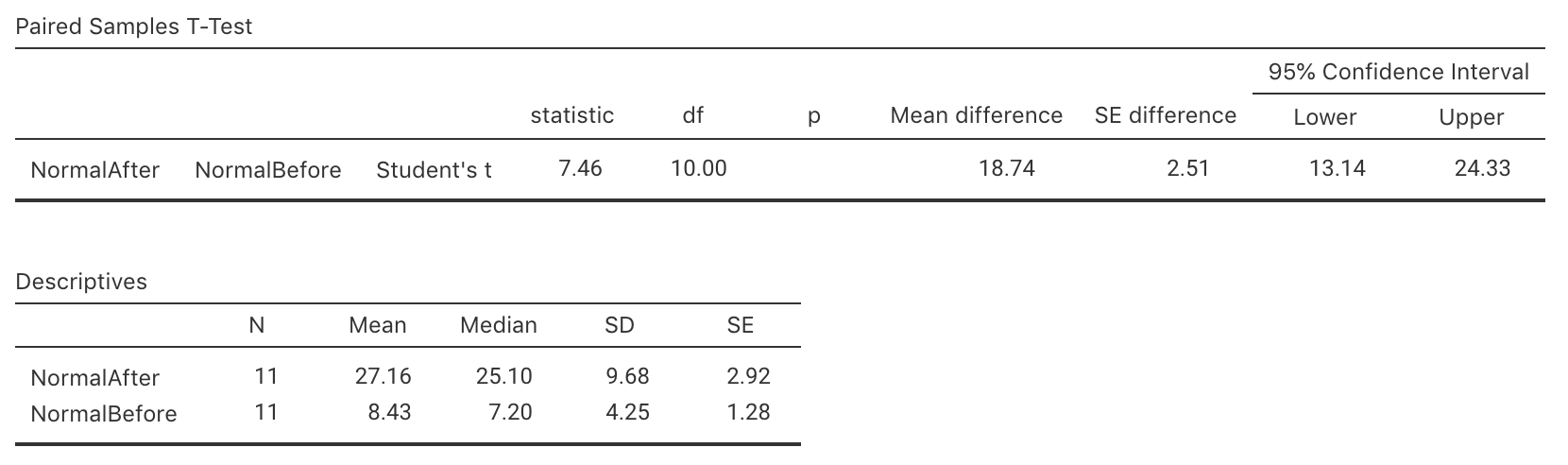
FIGURE 9.11: Output from jamovi for the fun run example, partially edited
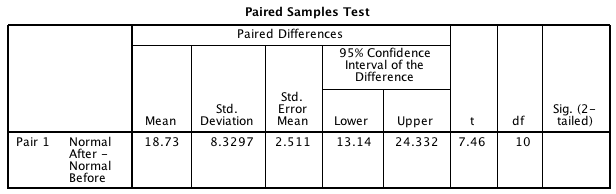
FIGURE 9.12: Output from SPSS for the fun run example, partially edited
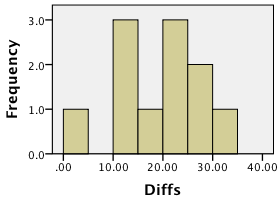
FIGURE 9.13: Histogram of differences for the fun run example