6.5 Random coin tosses
Use this website at RANDOM.org (at the bottom of the page, keep pressing Flip again to repeat) to flip ten Australian one-dollar coins at random (see Fig. 6.2).
FIGURE 6.2: Using the online random coin-tosser
Repeat this process numerous times (if you are in a class, each student can repeat the process numerous times so you get a large number of tosses), and complete the following table:
| Proportion of heads in 10 tosses | How many times observed |
|---|---|
| 0.0 (0 heads) | |
| 0.1 (1 head) | |
| 0.2 (2 heads) | |
| 0.3 (3 heads) | |
| 0.4 (4 heads) | |
| 0.5 (5 heads) | |
| 0.6 (6 heads) | |
| 0.7 (7 heads) | |
| 0.8 (8 heads) | |
| 0.9 (9 heads) | |
| 1.0 (10 heads) | |
- Use this data to create a histogram of the proportion of heads. How would you describe the histogram?
- I did the same thing, but I repeated the process of tossing \(10\) coins \(400\) times. My histogram is shown in Fig. 6.3. How would you describe the histogram?
- Sketch the theoretical sampling distribution of the sampling proportion.
- How would this sampling distribution change if we looked the proportion of heads in \(50\) tosses of a coin?
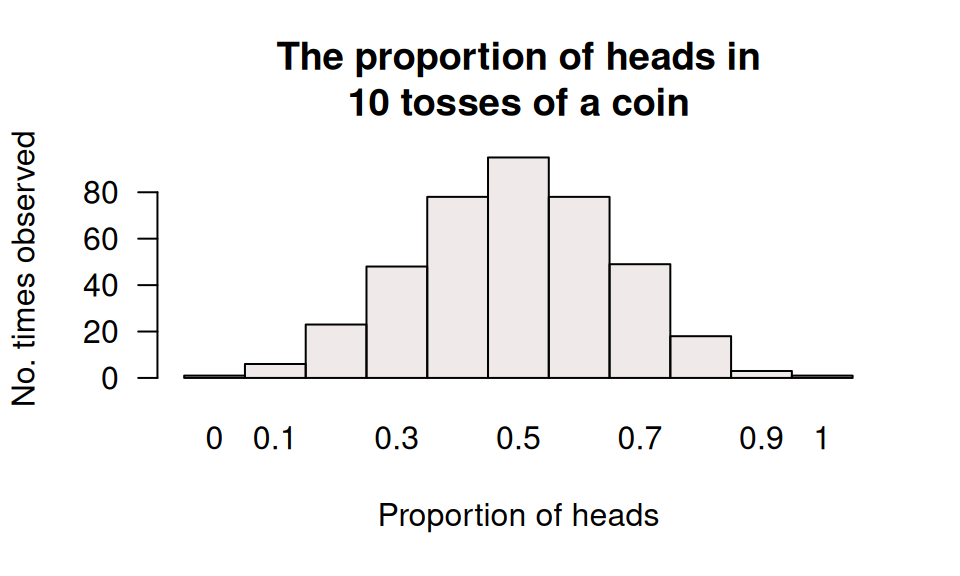
FIGURE 6.3: The histogram of the proportion of heads in \(10\) tosses, for \(400\) repetitions.