7.8 Optional questions
These questions are optional; e.g., if you need more practice, or you are studying for the exam. (Answers are available in Sect. A.7.)
7.8.1 Optional: CI for one mean
This question has a video solution in the online book, so you can hear and see the solution.
Shortly after metric units were introduced to Australia in 1977, a lecturer wondered how accurately students could estimate lengths using the metric measurements (Hand et al. 1996).
The aim of the study was to determine if, on average, students could correctly guess the width of the hall (which was \(13.1\) m).
To answer the RQ, a group of \(n = 44\) students were asked to estimate the width of the lecture hall to the nearest metre (data provided by Prof. Lewis). The data are given in Table 7.1.
The data were entered into software, producing the output in Fig. 7.7 (jamovi) and Fig. 7.8 (SPSS).
| 8 | 9 | 10 | 10 | 10 | 10 | 10 | 10 | 11 | 11 | 11 | 11 | 12 | 12 | 13 |
| 13 | 13 | 14 | 14 | 14 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 16 | 16 |
| 16 | 17 | 17 | 17 | 17 | 18 | 18 | 20 | 22 | 25 | 27 | 35 | 38 | 40 |
- What is the value of \(\bar{x}\)?
- What are the values of \(s\) and \(\text{s.e.}(\bar{x})\)? Explain the difference in the meaning of the two terms.
- Write down the \(95\)% CI for the population estimate (see Fig.
7.7 (jamovi) or Fig. 7.8 (SPSS)). - What conditions must be met for this test to be statistically valid?
- Is it reasonable to assume the statistical validity conditions are satisfied? The histogram in Fig. 7.6 may help.
- Do you think students were very good at estimating the width of the hall using metric units? Explain.
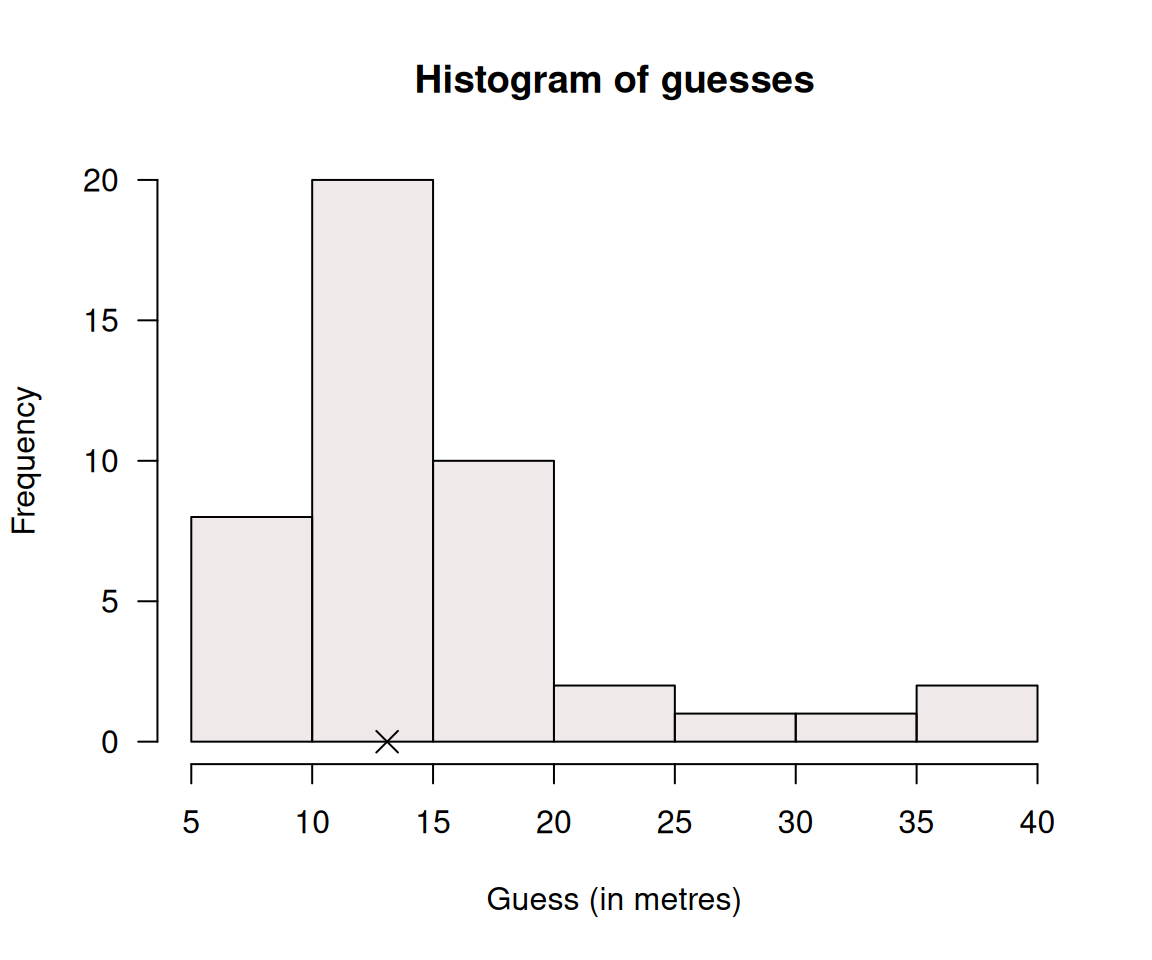
FIGURE 7.6: Histogram for the estimates of the width of a hall
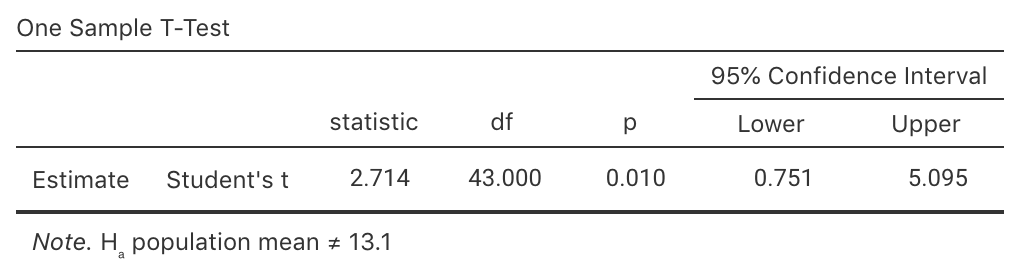
FIGURE 7.7: jamovi output for the estimates of the width of a hall in metres
FIGURE 7.8: SPSS output for the estimates of the width of a hall in metres
7.8.2 Optional: CI for one proportion
This question has a video solution in the online book, so you can hear and see the solution.
The timing of pubertal maturation can vary, which can have impacts upon behaviour. One research project studied
...the relationships between maturational timing and body image, school behavior, and deviance
--- Duncan et al. (1985), (p. 231)
Sample data were collected from
...children and youth of the entire United States drawn by the National Center for Health Statistics... known as the National Health Examination Survey (1966--1970). Data were collected on \(5\ 735\) adolescents' physical and psychological status...
- What type of research question is being answered: descriptive, relational, repeated-measures of correlational? Explain.
- For the \(2\ 864\) males in the sample, \(352\) were classified as maturing late. Compute the sample estimate of the population proportion of males who mature late.
- Compute the precision of this estimate (that is, the standard error).
- Compute an approximate \(95\)% confidence interval for the population proportion of boys that mature late based on the sample proportion.
- Confirm that the conditions necessary for this calculation to be statistically valid are met.
- If the researchers wished to estimate the true proportion of boys that mature late to within give-or-take \(0.02\) with \(95\)% confidence, would a larger or smaller sample be needed? Explain.
- If the researchers wished to estimate the proportion of boys maturing late within give-or-take \(0.02\) with \(95\)% confidence, what size sample would be needed?
7.8.3 Optional: CI for mean differences (paired data)
Wave power has been considered as a source of energy since 1890, but the engineering necessary to successfully and practically harness this energy is complex.
To understand one method of harnessing this energy, one study (Hand et al. 1996) examined the bending stress (in Newton--metres) in part of a device used to generate electricity from wave power.
Two different mooring types were compared (Table 7.2) in \(18\) different sea states.
| Method 1 | Method 2 | Differences |
|---|---|---|
| 2.23 | 1.82 | 0.41 |
| 2.55 | 2.42 | 0.13 |
| 7.99 | 8.26 | -0.27 |
| 4.09 | 3.46 | 0.63 |
| 9.62 | 9.77 | -0.15 |
| 1.59 | 1.4 | 0.19 |
| 8.98 | 8.88 | 0.1 |
| 0.82 | 0.87 | -0.05 |
| 10.83 | 11.2 | -0.37 |
| 1.54 | 1.33 | 0.21 |
| 10.75 | 10.32 | 0.43 |
| 5.79 | 5.87 | -0.08 |
| 5.91 | 6.44 | -0.53 |
| 5.79 | 5.87 | -0.08 |
| 5.5 | 5.3 | |
| 9.96 | 9.82 | |
| 1.92 | 1.69 | |
| 7.38 | 7.41 |
- Explain why these data should be analysed as mean differences.
- Compute the sample differences (most have been done for you).
- Using the statistics mode on your calculator, compute the sample mean and the sample standard deviation of these differences.
- Compute the standard error of the mean difference. What does this value mean?
- Compute an approximate \(95\)% CI for the population mean difference in two methods.
- What conditions must be met for this CI to be statistically valid?
- Is it reasonable to assume the CI is statistically valid? Draw a stem-and-leaf plot to check.
- Do you think the mooring types are really different? Explain.
7.8.4 Optional: CI for mean differences (paired data)
This question has a video solution in the online book, so you can hear and see the solution.
After a number of runners collapsed near the finish of the Tyneside annual Great North Run, researchers decided to study the role of \(\beta\) endorphins as a factor in the collapses. (\(\beta\) endorphins are a peptide which suppress pain.)
A study (Dale et al. 1987) examined what happened with plasma \(\beta\) endorphins during fun runs: how much do the concentrations change, on average?
The researchers recorded the plasma \(\beta\) concentrations in fun runners (participating in the Tyneside Great North Run). Eleven runners (who did not collapse) had their plasma \(\beta\) concentrations measured (in pmol/litre) before and after the race (Table 7.3.)
| Before race | After race | Difference |
|---|---|---|
| 4.3 | 29.6 | 25.3 |
| 4.6 | 25.1 | 20.5 |
| 5.2 | 15.5 | 10.3 |
| 5.2 | 29.6 | 24.4 |
| 6.6 | 24.1 | 17.5 |
| 7.2 | 37.8 | 30.6 |
| 8.4 | 20.1 | 11.7 |
| 9.0 | 21.9 | 12.9 |
| 10.4 | 14.2 | 3.8 |
| 14.0 | 34.6 | 20.6 |
| 17.8 | 46.2 | 28.4 |
The 'usual' value for \(\beta\) endorphines is usually less than about 11 pmol/litre.
- What do \(\mu_d\) and \(\bar{d}\) represent in this context?
- Explain why these data should be analysed as mean differences.
- Compute the changes in plasma \(\beta\) endorphin concentration during the run (i.e. the 'differences'). (Although it doesn't really matter, why does it probably makes more sense to compute the after values minus the before values?)
- Using the statistics mode on your calculator, compute the sample mean difference \(\bar{d}\) and the sample standard deviation of the differences.
- Compute the standard error of the mean difference. Explain what this means in this context.
- If another sample of eleven runners were studied, would the same sample mean difference be computed? How much variation would be expected in the sample means found from different samples?
- Compute an approximate \(95\)% confidence interval for the population mean difference in plasma \(\beta\) concentrations.
- Construct a one-sentence statement that communicates a \(95\)% CI for the population difference in plasma \(\beta\) concentrations.
- What conditions must be met for this CI to be statistically valid?
- Is it reasonable to assume the CI is statistically valid? Construct a stem-and-leaf plot to help.
- Do you think the population plasma \(\beta\) concentration changes during the race, on average? Explain.
- Suppose the researchers wished to estimate the change in plasma \(\beta\) endorphin concentrations to within \(2.5\) pmol/litre, with \(95\)% confidence. What size sample would be necessary?