5.4 Understanding correlations

Answer the following questions, referring to Fig. 5.8. The four correlation coefficients \(r\) are:

A: \(r = -0.95\)

B: \(r = 0.12\)

C: \(r = 0.75\)

D: \(r = 0.94\)

For two plots, a correlation is not suitable.

Determine which plot corresponds to which correlation coefficient (and for which two plots a correlation coefficient is not suitable).
Think of an example of two quantitative variables that might produce a plot with a direction similar to Plot 1.
Think of an example of two quantitative variables that might produce a plot with a direction similar to Plot 2.
Compute the values of \(R^2\) for each plot identified in Part 1 of this question.

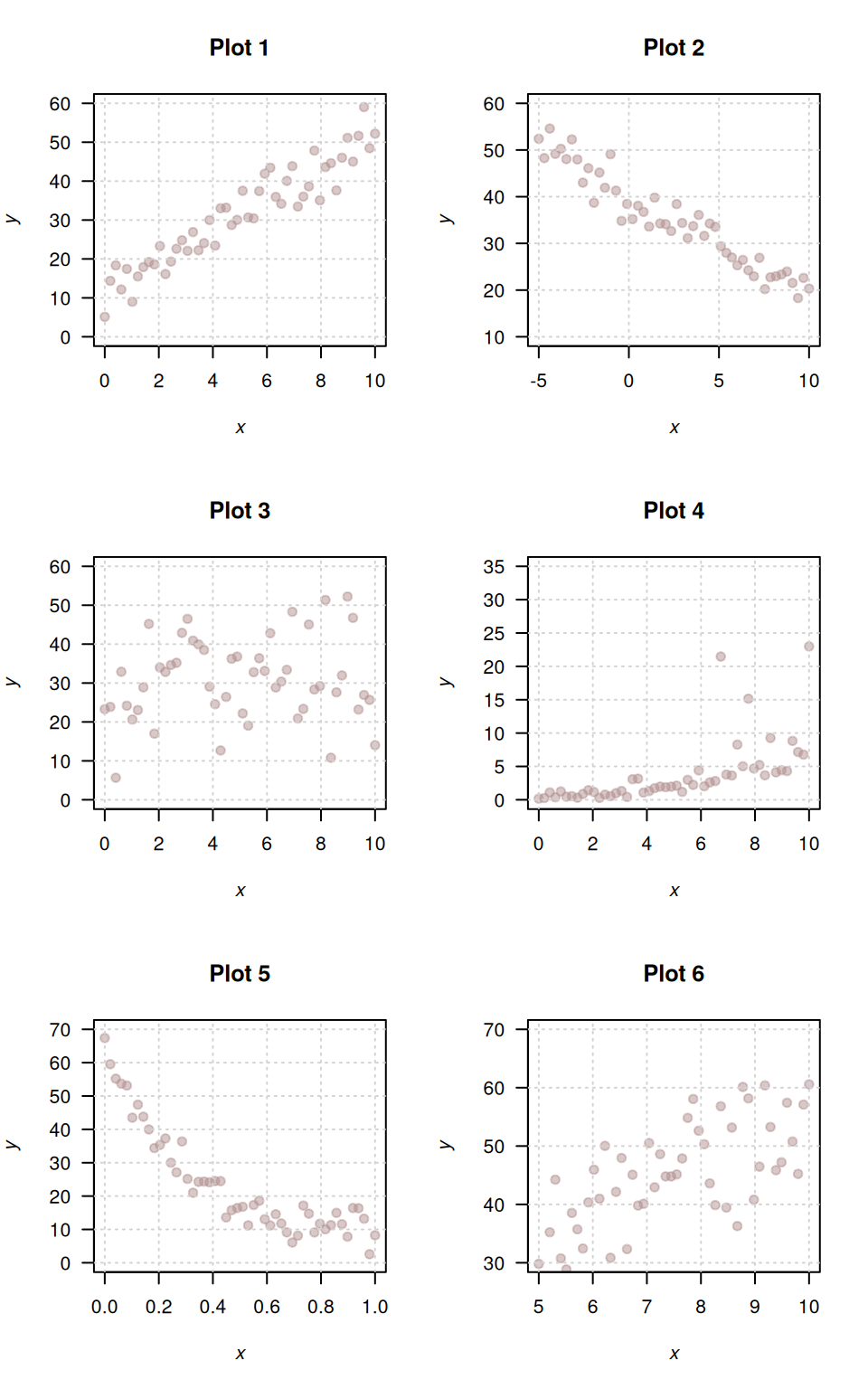
FIGURE 5.8: Six different scatterplots