A.12 Answer: TW 12 tutorial
Answers for Sect. 12.2
- No answer. But a line is fine for Plots 1, 2, 6 and 3 (but very weak!), but not for Plots 4 and 5.
- My very rough slope estimates are:
Plot 1: \((50-10)/10 \approx 4\); Plot 2: \((20 - 50)/15 \approx -2\); Plot 3: \(0\); Plot 6: \((55 - 35)/5 = 4\). - My very rough intercept estimates are: Plot 1: \(8\); Plot 2: \(40\); Plot 3: \(32\); Plot 6: \(10\).
- My very rough estimates are: Plot 1; \(\hat{y} = 8 + 4x\); Plot 2: \(\hat{y} = 40 - 2x\); Plot 3: \(\hat{y} = 32\); Plot 6: \(\hat{y} = 10 + 4x\).
Answers for Sect. 12.3
- Approximately linear, negative, reasonably strong.
- Condition, extras (air con, etc.), sedan/hatch, colour, when rego due, new/old tyres, location, etc.
- No answer.
- Looks to be expensive, as $15,000 would be above the line (at least for the line I'd draw).
- Probably $3900.
- My guess is about \(b_0\approx 17\) or $17,000. This would mean the average price of a 2014 second-hand Corolla can be expected to be about $17,000.
- \(b_1 = (1 - 17)/(16 - 0)\approx -1\). That is, the price reduces by about $1000 each year older the Corolla gets.
- Using the above, we have \(\hat{y} = 17 - x\) approximately. Guessing the regression line won't, of course, produce this level of precision, so anything close-ish to this is fine.
- \(\hat{y} = 16.54 - 0.96x\) (jamovi) or \(\hat{y} = 16.536 - 0.963x\) (SPSS), where \(y\) is the price in thousands of dollars, and \(x\) is the age in years.
- \(r = -0.929\), and so \(R^2 = (-0.929)^2 = 0.863\), or about \(86\)%, so about \(86\)% of the variation in prices can be explained by age alone. The rest can be explained by the car's condition, odometer reading, accessories, service history, etc.
- jamovi: \(\hat{y} = 16.54 - (0.96\times 20) = -2.66\), or -$2660.
SPSS: \(\hat{y} = 16.536 - (0.963\times 20) = -2.72\), or -$2720.
This is clearly silly, as we are extrapolating. - Hardly need a test... \(H_0\): \(\beta_1 = 0\) vs \(H_1\): \(\beta_1 < 0\). From output, \(t = -15.059\), and \(P = 0.000/2 = 0.000\), so \(P < 0.0001\): very strong evidence that older cars fetch lower second-hand prices, on average.
- \(-0.963 \pm (2\times 0.064)\), or \(-0.963\pm 0.128\), or from \(-1.091\) to \(-0.835\).
- Looks the same really, just reflected left-to-right.
- Size of \(r\) won't change, sign from negative to positive; i.e., \(r = 0.93\).
- Value of \(R^2\) will be the same.
- Slope will be the same except sign will change (in both cases, the values on the horizontal axis are one year apart).
- Intercept will change a lot... it is the predicted value of the price if the line is extended to year \(0\) (which is, of course, meaningless).
Answers for Sect. 12.4
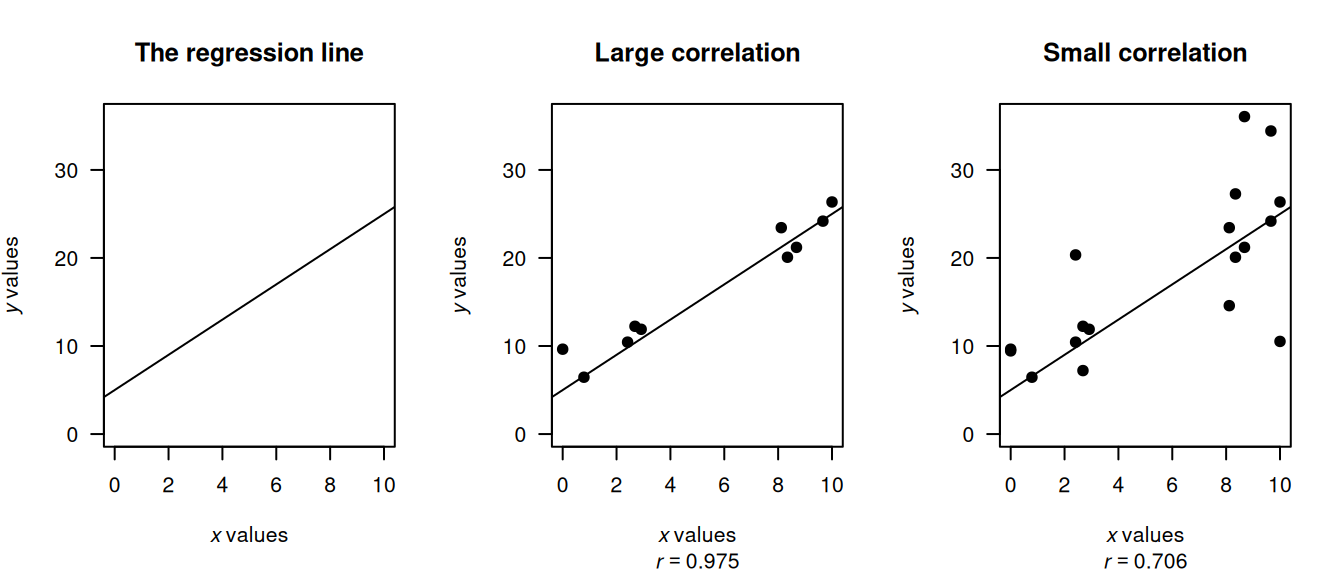
FIGURE A.1: Plots giving different correlations.