8.4 Tests for one mean

In 2011, Eagle Boys' Pizza ran a campaign that claimed that Eagle Boys' pizzas were 'Real size $12$ -inch large pizzas' (Dunn 2012). Eagle Boys' made the data from the campaign publicly available.

A summary of the diameters of a sample of $125$ of their large pizzas is shown in Fig. 8.1. We would like to test the company's claim, and ask the RQ:

For Eagle Boys' pizzas, is mean diameter actually $12$ inches, or not?

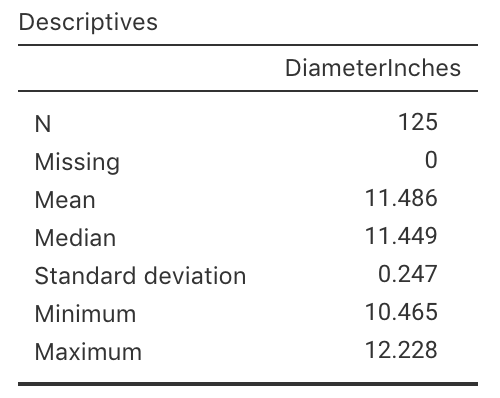
FIGURE 8.1: Summary statistics for the diameter of Eagle Boys' large pizzas; jamovi

What is the parameter of interest?
Write down the values of $\bar{x}$ and $s$ .
Determine the value of the standard error of the mean.
Explain the difference in meaning between $s$ and $\text{s.e.}(\bar{x})$ in this context.
Write the hypotheses to test if the mean pizza diameter is $12$ inches.
Is the alternative hypothesis one- or two-tailed? Why?
Draw the normal distribution that shows how the sample mean pizza diameter would vary by chance, even if the population mean diameter was $12$ inches.
Compute the $t$ -score for testing the hypotheses.
What is the approximate $P$ -value using the $68$ -- $95$ -- $99.7$ rule?
Write a conclusion. (The CI was found in the Teaching Week 7 tutorial.)
Is it reasonable to assume the statistical validity conditions are satisfied? How does Fig. 8.2 help, if at all?
Do you think that the pizzas do have a mean diameter of $12$ inches in the population, as Eagle Boys' claim? Explain.

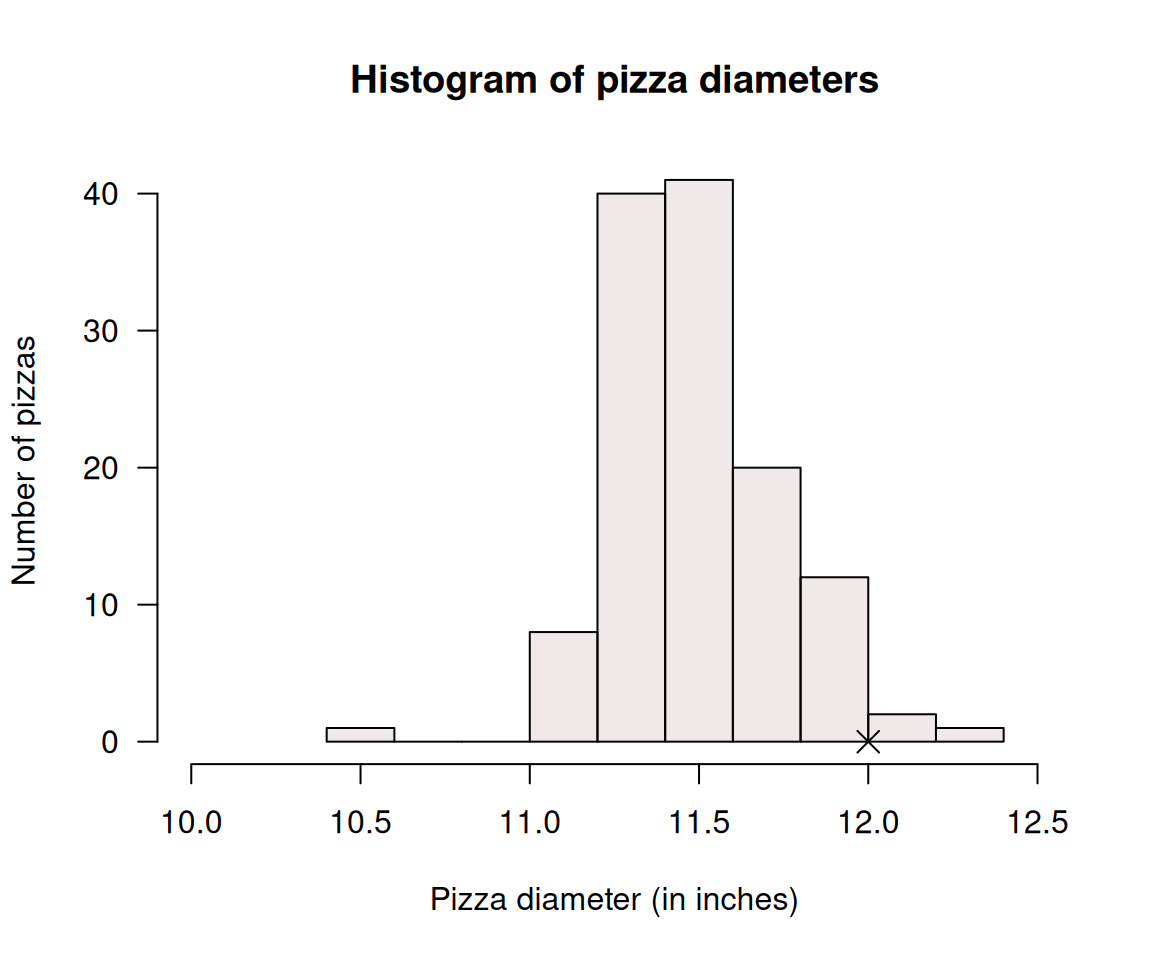
FIGURE 8.2: Histogram for the diameter of Eagle Boys' large pizzas. The cross represents the claimed diametet of $12$ inches.

References

Dunn PK. Assessing claims made by a pizza chain. Journal of Statistical Education [Internet]. 2012;20(1). Available from: www.amstat.org/publications/jse/v20n1/dunn.pdf.