2.5 Measures of model fit
In the Bayesian world, we don’t tend to appeal to the \(SS_{residual}\), the \(MS_{residual}\), or the standard error of estimate. We do sometimes, however, appeal to the \(R^2\). I’m not going to go into the technical details here, but you should be aware that the Bayesian \(R^2\) is not calculated the same as the OLS \(R^2\). If you want to dive in, check out the paper by Gelman, Goodrich, Gabry, and Ali. Here’s how to get it in brms.
bayes_R2(model4, summary = T) %>% round(digits = 3)
#> Estimate Est.Error Q2.5 Q97.5
#> R2 0.389 0.02 0.347 0.427Happily, it comes with 95% intervals, which will make the editors at APA journals happy. If you want to go beyond summary statistics and take a look at the full posterior, just set summary = F and data wrangle and plot as usual.
bayes_R2(model4, summary = F) %>%
as_tibble() %>%
ggplot(aes(x = R2)) +
geom_density(fill = "black", color = "transparent") +
scale_y_continuous(NULL, breaks = NULL) +
labs(title = expression(paste("Behold: The Bayesian ", italic("R")^{2}, " distribution for model 4")),
x = NULL) +
coord_cartesian(xlim = 0:1) +
theme_bw()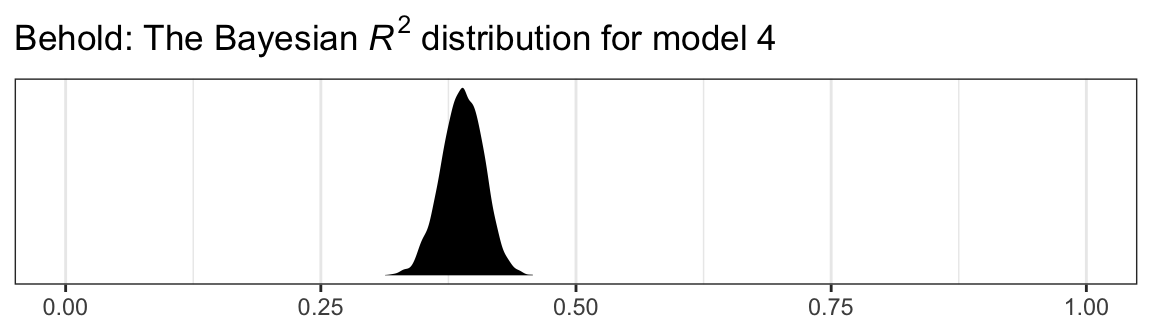
Another way we examine model fit is with graphical posterior predictive checks. Posterior predictive checking is a very general approach, which you might learn more about here or with a few keyword searches in on Gelman’s blog. One basic way is to use the model in order to simulate data and then compare those data with the original data–the basic idea being that good fitting models should produce data similar to the original data.
Recall how we’ve used fitted() to make regression lines and expected values? We’ll, now we’ll use predict() to simulate data based on our models.
predict(model4,
summary = F,
nsamples = 3) %>%
t() %>%
as_tibble() %>%
gather() %>%
mutate(key = str_replace(key, "V", "simulation ")) %>%
rename(govact = value) %>%
bind_cols(
bind_rows(
glbwarm %>% select(-govact),
glbwarm %>% select(-govact),
glbwarm %>% select(-govact))
) %>%
ggplot(aes(x = negemot, y = govact)) +
geom_jitter(height = .05, width = .05,
alpha = 1/2, size = 1/3) +
coord_cartesian(ylim = 0:9) +
theme_bw() +
facet_wrap(~key, ncol = 3)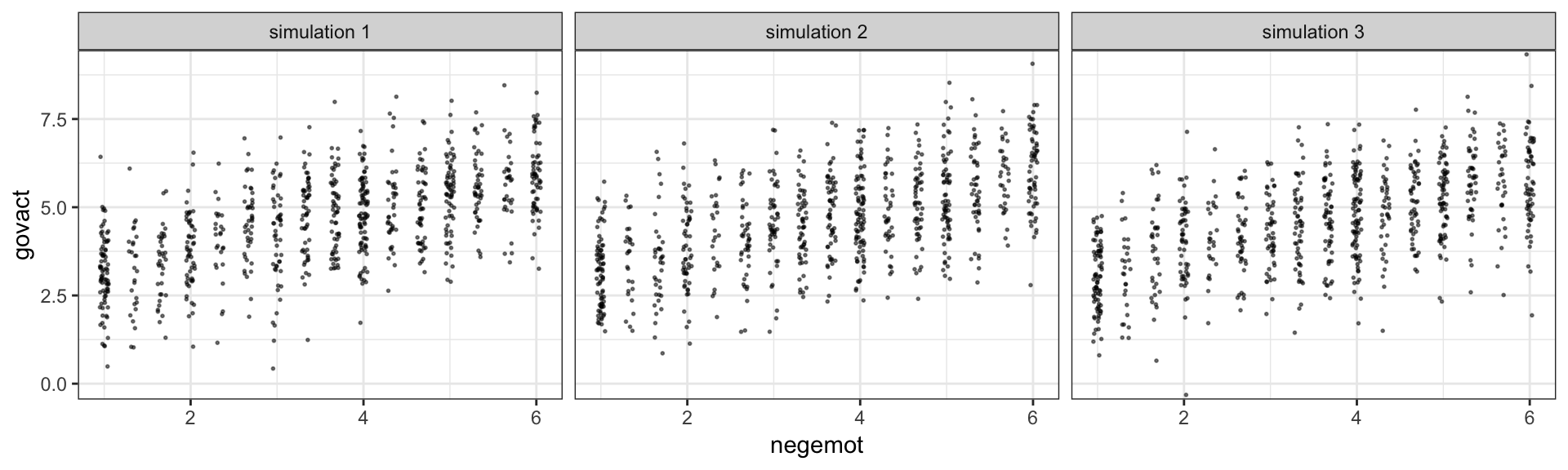
The question is, do these simulated data sets look like the original data? Let’s see.
glbwarm %>%
ggplot(aes(x = negemot, y = govact)) +
geom_jitter(height = .05, width = .05,
alpha = 1/2, size = 1/3) +
coord_cartesian(ylim = 0:9) +
theme_bw()
Overall, the simulations aren’t bad. But in all three govact tends to veer above 7.5, which is where the original data appear to be bounded. But otherwise the overall shape is pretty close, at least with respect to negemot.
There’s nothing special about three simulations. Three is just more than one and gives you a sense of the variance across simulations. Also, we only examined the model fit with respect to negemot. Since there are other variables in the model, we might also assess the model based on them.
Another method is with the brms::pp_check() function, which allows users to access a variety of convenience functions from the bayesplot package. Here we’ll use the default settings and just tack on theme_bw() for aesthetics.
pp_check(model4) +
theme_bw()
#> Using 10 posterior samples for ppc type 'dens_overlay' by default.
What we did was simulate 10 data sets worth of govact values, plot their densities (i.e., the thin blue lines) and compare them with the density of the original govact values. What we want is for the thin blue lines to largely align with the thick blue line. Though not perfect, the simulations from our model4 did a pretty okay job of reproducing the original govact distribution. For more ideas on this method, see the brms reference manual and this vignette for the bayesplot package.