5.2 Example using the presumed media influence study
Here we load a couple necessary packages, load the data, and take a glimpse().
library(tidyverse)
pmi <- read_csv("data/pmi/pmi.csv")
glimpse(pmi)## Observations: 123
## Variables: 6
## $ cond <int> 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0...
## $ pmi <dbl> 7.0, 6.0, 5.5, 6.5, 6.0, 5.5, 3.5, 6.0, 4.5, 7.0, 1.0, 6.0, 5.0, 7.0, 7.0, 7.0, 4.5, 3.5...
## $ import <int> 6, 1, 6, 6, 5, 1, 1, 6, 6, 6, 3, 3, 4, 7, 1, 6, 3, 3, 2, 4, 4, 6, 7, 4, 5, 4, 6, 5, 5, 7...
## $ reaction <dbl> 5.25, 1.25, 5.00, 2.75, 2.50, 1.25, 1.50, 4.75, 4.25, 6.25, 1.25, 2.75, 3.75, 5.00, 4.00...
## $ gender <int> 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0, 0, 0, 1...
## $ age <dbl> 51.0, 40.0, 26.0, 21.0, 27.0, 25.0, 23.0, 25.0, 22.0, 24.0, 22.0, 21.0, 23.0, 21.0, 22.0...Let’s load brms.
library(brms)Bayesian correlations, recall, just take an intercepts-only multivariate model.
model1 <-
brm(data = pmi, family = gaussian,
cbind(pmi, import) ~ 1,
chains = 4, cores = 4)A little indexing with the posterior_summary() function will get us the Bayesian correlation with its posterior \(SD\) and intervals.
posterior_summary(model1)["rescor__pmi__import", ] %>% round(digits = 3)## Estimate Est.Error Q2.5 Q97.5
## 0.274 0.084 0.103 0.432As with single mediation models, the multiple mediation model requires we carefully construct the formula for each criterion. We’ll continue to use the multiple bf() approach.
m1_model <- bf(import ~ 1 + cond)
m2_model <- bf(pmi ~ 1 + cond)
y_model <- bf(reaction ~ 1 + import + pmi + cond)And now we fit the model.
model2 <-
brm(data = pmi, family = gaussian,
y_model + m1_model + m2_model + set_rescor(FALSE),
chains = 4, cores = 4)print(model2, digits = 3)## Family: MV(gaussian, gaussian, gaussian)
## Links: mu = identity; sigma = identity
## mu = identity; sigma = identity
## mu = identity; sigma = identity
## Formula: reaction ~ 1 + import + pmi + cond
## import ~ 1 + cond
## pmi ~ 1 + cond
## Data: pmi (Number of observations: 123)
## Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
## total post-warmup samples = 4000
##
## Population-Level Effects:
## Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
## reaction_Intercept -0.153 0.538 -1.180 0.907 4000 0.999
## import_Intercept 3.907 0.211 3.495 4.318 4000 0.999
## pmi_Intercept 5.377 0.167 5.055 5.705 4000 1.000
## reaction_import 0.324 0.074 0.178 0.467 4000 0.999
## reaction_pmi 0.396 0.095 0.210 0.587 4000 1.000
## reaction_cond 0.106 0.241 -0.358 0.575 4000 1.000
## import_cond 0.628 0.312 0.038 1.236 4000 0.999
## pmi_cond 0.477 0.235 0.006 0.951 4000 1.000
##
## Family Specific Parameters:
## Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
## sigma_reaction 1.304 0.086 1.152 1.482 4000 0.999
## sigma_import 1.733 0.116 1.526 1.977 4000 1.000
## sigma_pmi 1.319 0.083 1.168 1.492 4000 1.000
##
## Samples were drawn using sampling(NUTS). For each parameter, Eff.Sample
## is a crude measure of effective sample size, and Rhat is the potential
## scale reduction factor on split chains (at convergence, Rhat = 1).Because we have three criteria, we’ll have three Bayesian \(R^2\) posteriors.
library(ggthemes)
bayes_R2(model2, summary = F) %>%
as_tibble() %>%
gather() %>%
mutate(key = str_remove(key, "R2_")) %>%
ggplot(aes(x = value, color = key, fill = key)) +
geom_density(alpha = .5) +
scale_color_ptol() +
scale_fill_ptol() +
scale_y_continuous(NULL, breaks = NULL) +
coord_cartesian(xlim = 0:1) +
labs(title = expression(paste("Our ", italic("R")^{2}, " distributions")),
subtitle = "The densities for import and pmi are asymmetric, small, and largely overlapping. The density for reaction is Gaussian and\nmore impressive in magnitude.",
x = NULL) +
theme_minimal() +
theme(legend.title = element_blank())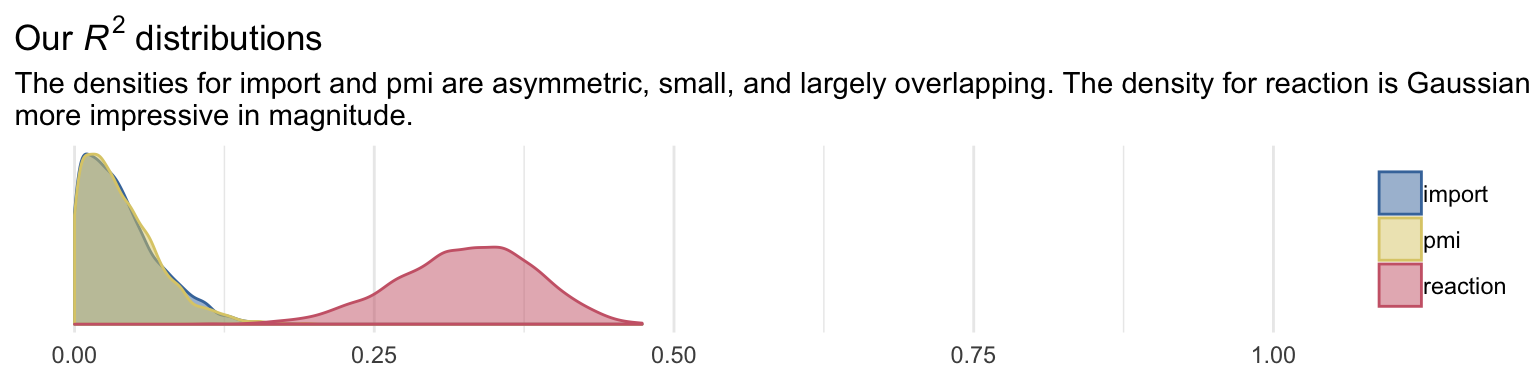
It’ll take a bit of data wrangling to rename our model parameters to the \(a\), \(b\)… configuration. We’ll compute the indirect effects and \(c\), too.
post <- posterior_samples(model2)
post<-
post %>%
mutate(a1 = b_import_cond,
a2 = b_pmi_cond,
b1 = b_reaction_import,
b2 = b_reaction_pmi,
c_prime = b_reaction_cond) %>%
mutate(a1b1 = a1*b1,
a2b2 = a2*b2) %>%
mutate(c = c_prime + a1b1 + a2b2)Here are their summaries. Since Bayesians use means, medians, and sometimes the mode to describe the central tendencies of a parameter, this time we’ll mix it up and just use the median.
post %>%
select(a1:c) %>%
gather() %>%
group_by(key) %>%
summarize(median = median(value),
ll = quantile(value, probs = .025),
ul = quantile(value, probs = .975)) %>%
mutate_if(is_double, round, digits = 3)## # A tibble: 8 x 4
## key median ll ul
## <chr> <dbl> <dbl> <dbl>
## 1 a1 0.627 0.038 1.24
## 2 a1b1 0.194 0.011 0.445
## 3 a2 0.477 0.006 0.951
## 4 a2b2 0.18 0.003 0.423
## 5 b1 0.324 0.178 0.467
## 6 b2 0.395 0.21 0.587
## 7 c 0.498 -0.018 1.04
## 8 c_prime 0.1 -0.358 0.575post %>%
mutate(dif = a1b1*b1) %>%
summarize(median = median(dif),
ll = quantile(dif, probs = .025),
ul = quantile(dif, probs = .975)) %>%
mutate_if(is_double, round, digits = 3)## median ll ul
## 1 0.061 0.002 0.183In the middle paragraph of page 158, Hayes showd how the mean difference in imprt between the two cond groups multiplied by b1, the coefficient of import predicting reaction, is equal to the a1b1 indirect effect. He did that with simple algebra using the group means and the point estimates.
Let’s follow along. First, we’ll get those two group means and save them as numbers to arbitrary precision.
(
import_means <-
pmi %>%
group_by(cond) %>%
summarize(mean = mean(import))
)## # A tibble: 2 x 2
## cond mean
## <int> <dbl>
## 1 0 3.91
## 2 1 4.53(cond_0_import_mean <- import_means[1, 2] %>% pull())## [1] 3.907692(cond_1_import_mean <- import_means[2, 2] %>% pull())## [1] 4.534483Here we follow the formula in the last sentence of the paragraph and then compare the results to the posterior for a1b1.
post %>%
# Using his formula to make our new vector, `handmade a1b1`
mutate(`handmade a1b1` = (cond_1_import_mean - cond_0_import_mean)*b1) %>%
# Here's all the usual data wrangling
select(a1b1, `handmade a1b1`) %>%
gather() %>%
group_by(key) %>%
summarize(mean = mean(value),
median = median(value),
ll = quantile(value, probs = .025),
ul = quantile(value, probs = .975)) %>%
mutate_if(is_double, round, digits = 3)## # A tibble: 2 x 5
## key mean median ll ul
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 a1b1 0.203 0.194 0.011 0.445
## 2 handmade a1b1 0.203 0.203 0.112 0.293Yep, Hayes’s formula is spot on at the mean. But the distributions are distinct. They differ slightly at the median and vastly in the widths of the posterior intervals. I’m no mathematician, so take this with a grain of salt, but I suspect this has to do with how we used fixed values (i.e., the difference of the subsample means) to compute handmade a1b1, but all the components in a1b1 were estimated.
Here we’ll follow the same protocol for a2b2.
(
pmi_means <-
pmi %>%
group_by(cond) %>%
summarize(mean = mean(pmi))
)## # A tibble: 2 x 2
## cond mean
## <int> <dbl>
## 1 0 5.38
## 2 1 5.85cond_0_pmi_mean <- pmi_means[1, 2] %>% pull()
cond_1_pmi_mean <- pmi_means[2, 2] %>% pull()post %>%
mutate(`handmade a2b2` = (cond_1_pmi_mean - cond_0_pmi_mean)*b2) %>%
select(a2b2, `handmade a2b2`) %>%
gather() %>%
group_by(key) %>%
summarize(mean = mean(value),
median = median(value),
ll = quantile(value, probs = .025),
ul = quantile(value, probs = .975)) %>%
mutate_if(is_double, round, digits = 3)## # A tibble: 2 x 5
## key mean median ll ul
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 a2b2 0.189 0.18 0.003 0.423
## 2 handmade a2b2 0.189 0.188 0.1 0.28To get the total indirect effect as discussed on page 160, we simply add the a1b1 and a2b2 columns.
post <-
post %>%
mutate(total_indirect_effect = a1b1 + a2b2)
post %>%
select(total_indirect_effect) %>%
summarize(mean = mean(total_indirect_effect),
median = median(total_indirect_effect),
ll = quantile(total_indirect_effect, probs = .025),
ul = quantile(total_indirect_effect, probs = .975)) %>%
mutate_if(is_double, round, digits = 3)## mean median ll ul
## 1 0.393 0.388 0.115 0.701To use the equations on the top of page 161, we’ll just work directly with the original vectors in post.
post %>%
mutate(Y_bar_given_X_1 = b_import_Intercept + b_reaction_cond*1 + b_reaction_import*b_import_Intercept + b_reaction_pmi*b_pmi_Intercept,
Y_bar_given_X_0 = b_import_Intercept + b_reaction_cond*0 + b_reaction_import*b_import_Intercept + b_reaction_pmi*b_pmi_Intercept) %>%
mutate(`c_prime by hand` = Y_bar_given_X_1 - Y_bar_given_X_0) %>%
select(c_prime, `c_prime by hand`) %>%
gather() %>%
group_by(key) %>%
summarize(mean = mean(value),
median = median(value),
ll = quantile(value, probs = .025),
ul = quantile(value, probs = .975))## # A tibble: 2 x 5
## key mean median ll ul
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 c_prime 0.106 0.100 -0.358 0.575
## 2 c_prime by hand 0.106 0.100 -0.358 0.575We computed c a while ago.
post %>%
summarize(mean = mean(c),
median = median(c),
ll = quantile(c, probs = .025),
ul = quantile(c, probs = .975))## mean median ll ul
## 1 0.4989729 0.4980823 -0.01773472 1.038924And c minus c_prime is straight subtraction.
post %>%
mutate(`c minus c_prime` = c - c_prime) %>%
summarize(mean = mean(`c minus c_prime`),
median = median(`c minus c_prime`),
ll = quantile(`c minus c_prime`, probs = .025),
ul = quantile(`c minus c_prime`, probs = .975))## mean median ll ul
## 1 0.3928318 0.3878582 0.1153838 0.7005085