11.3 Example: Hiding your feelings from your work team
Here we load a couple necessary packages, load the data, and take a glimpse().
library(tidyverse)
teams <- read_csv("data/teams/teams.csv")
glimpse(teams)## Observations: 60
## Variables: 4
## $ dysfunc <dbl> -0.23, -0.13, 0.00, -0.33, 0.39, 1.02, -0.35, -0.23, 0.39, -0.08, -0.23, 0.09, -0.29, -0....
## $ negtone <dbl> -0.51, 0.22, -0.08, -0.11, -0.48, 0.72, -0.18, -0.13, 0.52, -0.26, 1.08, 0.53, -0.19, 0.1...
## $ negexp <dbl> -0.49, -0.49, 0.84, 0.84, 0.17, -0.82, -0.66, -0.16, -0.16, -0.16, -0.16, 0.50, 0.84, 0.5...
## $ perform <dbl> 0.12, 0.52, -0.08, -0.08, 0.12, 1.12, -0.28, 0.32, -1.08, -0.28, -1.08, -0.28, -0.28, -0....Load the brms package.
library(brms)Recall that we fit mediation models in brms using multivariate syntax. In previous attempts, we’ve defined and saved the model components outside of the brm() function and then plugged then into brm() using their identifier. Just to shake things up a bit, we’ll just do all the steps right in brm(), this time.
model1 <-
brm(data = teams, family = gaussian,
bf(negtone ~ 1 + dysfunc) +
bf(perform ~ 1 + dysfunc + negtone + negexp + negtone:negexp) +
set_rescor(FALSE),
chains = 4, cores = 4)print(model1, digits = 3)## Family: MV(gaussian, gaussian)
## Links: mu = identity; sigma = identity
## mu = identity; sigma = identity
## Formula: negtone ~ 1 + dysfunc
## perform ~ 1 + dysfunc + negtone + negexp + negtone:negexp
## Data: teams (Number of observations: 60)
## Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
## total post-warmup samples = 4000
##
## Population-Level Effects:
## Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
## negtone_Intercept 0.026 0.062 -0.099 0.147 4000 1.000
## perform_Intercept -0.011 0.060 -0.131 0.104 4000 1.000
## negtone_dysfunc 0.619 0.166 0.290 0.951 4000 0.999
## perform_dysfunc 0.369 0.184 0.006 0.730 4000 1.000
## perform_negtone -0.440 0.134 -0.707 -0.178 4000 1.000
## perform_negexp -0.022 0.120 -0.260 0.213 4000 1.000
## perform_negtone:negexp -0.512 0.246 -0.992 -0.035 4000 1.000
##
## Family Specific Parameters:
## Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
## sigma_negtone 0.487 0.048 0.403 0.592 4000 1.000
## sigma_perform 0.460 0.045 0.383 0.557 4000 0.999
##
## Samples were drawn using sampling(NUTS). For each parameter, Eff.Sample
## is a crude measure of effective sample size, and Rhat is the potential
## scale reduction factor on split chains (at convergence, Rhat = 1).Our model summary coheres nicely with Table 11.1 and the formulas on page 409. Here are the \(R^2\) distribution summaries.
bayes_R2(model1) %>% round(digits = 3)## Estimate Est.Error Q2.5 Q97.5
## R2_negtone 0.192 0.077 0.047 0.344
## R2_perform 0.322 0.077 0.166 0.461On page 410 we get two sample means. Here they are:
mean(teams$negexp) %>% round(digits = 3)## [1] -0.008mean(teams$perform) %>% round(digits = 3)## [1] -0.032For our Figure 11.4 and other similar figures in this chapter, we’ll use spaghetti plots. Recall that with a spaghetti plots for linear models, we only need two values for the variable on the x-axis, rather than the typical 30+.
nd <-
tibble(dysfunc = mean(teams$dysfunc),
negtone = rep(c(-.8, .8), times = 3),
negexp = rep(quantile(teams$negexp, probs = c(.16, .50, .84)),
each = 2))Here’s our Figure 11.4, which uses only the first 40 HMC iterations for the spaghetti-plot lines.
fitted(model1,
newdata = nd,
resp = "perform",
summary = F) %>%
as_tibble() %>%
gather() %>%
mutate(iter = rep(1:4000, times = 2*3),
negtone = rep(rep(c(-.8, .8), times = 3),
each = 4000),
negexp = rep(rep(quantile(teams$negexp, probs = c(.16, .50, .84)),
each = 2),
each = 4000)) %>%
mutate(negexp = str_c("expresivity = ", negexp)) %>%
mutate(negexp = factor(negexp, levels = c("expresivity = -0.49", "expresivity = -0.06", "expresivity = 0.6"))) %>%
filter(iter < 41) %>%
ggplot(aes(x = negtone, y = value, group = iter)) +
geom_line(color = "skyblue3",
size = 1/4) +
coord_cartesian(xlim = c(-.5, .5),
ylim = c(-.6, .6)) +
labs(x = expression(paste("Negative Tone of the Work Climate (", italic(M), ")")),
y = "Team Performance") +
theme_bw() +
theme(panel.grid = element_blank(),
strip.background = element_rect(color = "transparent", fill = "transparent")) +
facet_wrap(~negexp)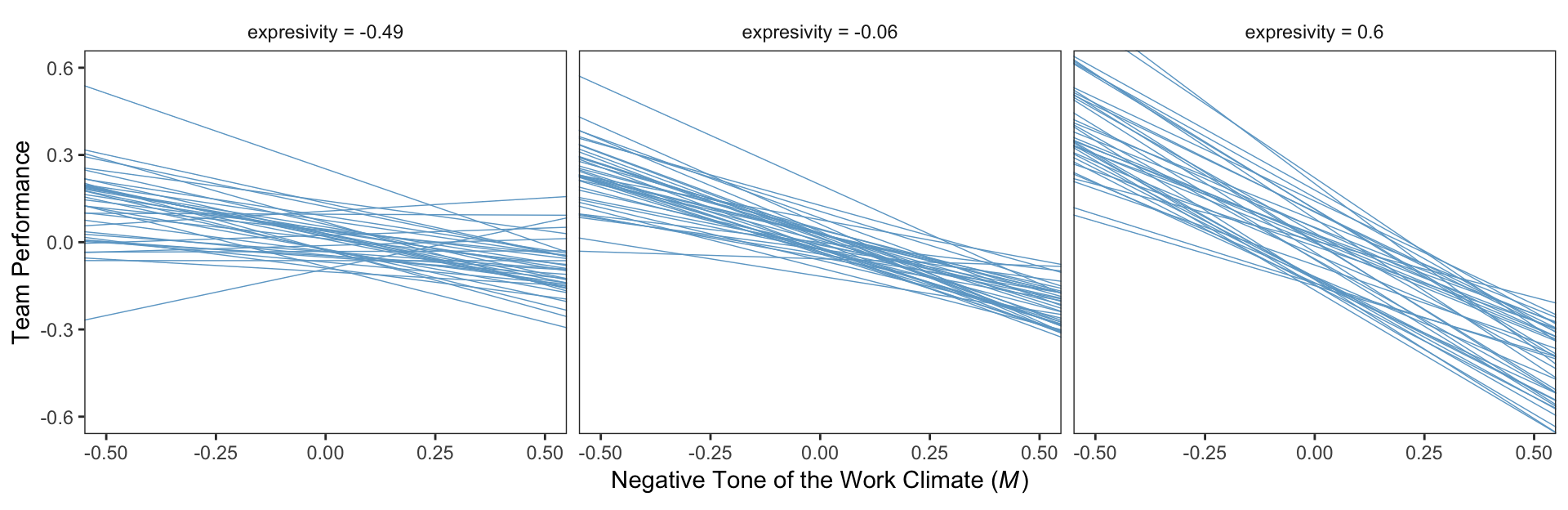
Also, the plot theme in this chapter is a nod to John Kruschke.